the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
A topographically controlled tipping point for complete Greenland ice sheet melt
Michele Petrini
Meike D. W. Scherrenberg
Laura Muntjewerf
Raymond Sellevold
Gunter R. Leguy
William H. Lipscomb
A major impact of anthropogenic climate change is the crossing of tipping points, which may have severe consequences such as the complete mass loss of the Greenland ice sheet (GrIS). At present, the GrIS is losing mass at an accelerated rate, largely due to a steep decrease in its surface mass balance (SMB; the balance between snow accumulation and surface ablation from melt and associated runoff). Previous work on the magnitude and nature of a threshold for GrIS complete melt remains controversial. Here, we explore a potential SMB threshold for complete melt of the GrIS; the impact and interplay of surface melt and glacial isostatic adjustment (GIA) in determining this threshold; and whether the GrIS exhibits characteristics commonly associated with tipping points, such as sensitivity to external forcing. To this end, we force the Community Ice Sheet Model v.2 (CISM2) by cycling different SMB climatologies previously calculated at multiple elevation classes with the Community Earth System Model v.2 (CESM2) in a two-way coupled CESM2–CISM2 transient simulation of the global climate and GrIS under high CO2 forcing. The SMB calculation in CESM2 has been evaluated with contemporary observations and high-resolution modelling and includes an advanced representation of surface melt and snow–firn processes.
We find a positive SMB threshold for complete GrIS melt of 230 ± 84 Gt yr−1, corresponding to a 60 % decrease in SMB and to a global mean warming of +3.4 K compared to pre-industrial CESM2–CISM2 simulated values. In our simulations, a small change in the initial SMB forcing (from 255 to 230 Gt yr−1) and global mean warming above pre-industrial levels (from +3.2 to +3.4 K) causes an abrupt change in the GrIS final volume (from 50 % mass to nearly complete deglaciation). This nonlinear behaviour is caused by the SMB–elevation feedback, which responds to changes in surface topography due to surface melt and GIA. The GrIS tips from ∼ 50 % mass towards nearly complete melt when the impact of melt-induced surface lowering outweighs that of GIA-induced bedrock uplift and the (initially positive) SMB becomes and remains negative for at least a few thousand years. We also find that the GrIS tips towards nearly complete melt when the ice margin in the central west unpins from a coastal region with high topography and SMB. We show that if we keep the SMB fixed (i.e. no SMB–elevation feedback) in this relatively confined region, the ice sheet retreat is halted and nearly complete GrIS melt is prevented even though the initial SMB forcing is past the threshold. Based on the minimum GrIS configuration in previous paleo-ice-sheet modelling studies, we suggest that the surface topography in the central west might have played a role in preventing larger GrIS loss during the last interglacial period ∼ 130–115 kyr BP.
- Article
(6055 KB) - Full-text XML
- BibTeX
- EndNote
The Greenland ice sheet (GrIS) is the largest freshwater reservoir in the Northern Hemisphere, currently storing 7.42 m of sea level equivalent (SLE; Morlighem et al., 2017). At present, the GrIS is losing mass at an accelerated pace, with ice loss rates over the last decade up to 6 times higher than in the 1980s (Mouginot et al., 2019). This is due to both atmospheric and ocean warming, causing enhanced surface melt and runoff, and increased ice discharge to the ocean (Mouginot et al., 2019). While until the late 1990s ice discharge had been the main source of ice loss (Shepherd et al., 2012), over the last 2 decades the contribution of surface processes has continuously increased, and as of today, 50 % of the overall GrIS mass loss increase is due to a decrease in surface mass balance (SMB; i.e. the balance between snow accumulation and surface ablation from melt and associated runoff) of around 160 Gt yr−1 (Mouginot et al., 2019; The IMBIE Team, 2020). In the future, the GrIS is expected to continue losing mass, with its contribution to global mean sea level (GMSL) largely depending on the amount of greenhouse gas forcing to the climate system (0.01–0.10 m under SSP1-2.6 (Shared Socioeconomic Pathway), 0.09–0.18 m under SSP5-8.5 relative to 1995–2014; see Fox-Kemper et al., 2021, and references therein). Regardless of the emission pathways, there is broad agreement that the GrIS mass loss over the 21st century and beyond will be dominated by SMB, while the influence of ice discharge to the ocean will diminish as the marine margins retreat to higher grounds (Robinson et al., 2012; Fürst et al., 2015; Goelzer et al., 2020; Gregory et al., 2020; Payne et al., 2021). Most of the projected decrease in SMB at the end of the century is attributed to an increase in surface melt and to the loss in refreezing capacity of the firn layer (Fettweis et al., 2013; Vizcaino et al., 2015; Sellevold and Vizcaíno, 2020; Noël et al., 2022).
As ice sheets are known to respond to surface changes over centuries and millennia rather than decades, an extremely important question is whether over longer timescales ongoing and projected 21st-century SMB changes could lead to complete GrIS melt, possibly through self-perpetuating mechanisms triggering an abrupt ice sheet response after crossing a tipping point (i.e. when a small change in forcing triggers a strongly nonlinear response in the internal dynamics of a system, qualitatively changing its future state; Lenton, 2011). When an ice sheet begins to thin and retreat at its margins due to surface melt, the positive SMB–elevation feedback is a major source for long-term mass loss: as the surface topography lowers due to ice thinning, the near-surface air temperature warms and leads to further ice melt. A number of paleo- and future-ice-sheet modelling studies agree in showing that this feedback is a self-amplifying mechanism that can drive GrIS partial or near-complete melt over multiple millennia (Robinson et al., 2012; Levermann et al., 2013; Plach et al., 2019; Gregory et al., 2020). While in this context ice loss can be further accelerated by the decrease in surface albedo associated with surface melt and ice retreat (SMB–albedo feedback; Box et al., 2012; Goelzer et al., 2016; Zeitz et al., 2021), other important negative feedbacks are also at play. Increasing surface temperatures and melt over the GrIS can be counterbalanced by larger snowfall and cloudiness as the ice sheet margins move towards the interior owing to regional atmospheric-circulation changes, orographic effects, and the higher relative humidity of warmer air masses (Gregory et al., 2020; Fyke et al., 2018). Another important process when investigating GrIS melt over multi-millennial timescales is glacial isostatic adjustment (GIA), which is the solid Earth's viscoelastic response to ice sheet unloading (Wake et al., 2016). Ice sheet thinning and retreat at the margins is followed, typically within a few centuries or millennia, by a GIA-induced bedrock uplift, with uplift rates and timing depending on the properties of the underlying lithosphere and asthenosphere (Milne et al., 2018). GIA-induced uplift can therefore limit and, in some cases, counterbalance the effect of the positive SMB–elevation feedback during ice sheet retreat. A recent study showed that asynchronous changes in GrIS surface topography due to surface melt and GIA can cause complex ice sheet regimes under sustained warming, including self-sustained oscillations or partial recovery after deglaciation (Zeitz et al., 2022).
To date, a few studies have attempted to assess thresholds for complete GrIS melt. Robinson et al. (2012) showed that while a negative integrated SMB is a sufficient condition for GrIS complete melt, not accounting for the evolving ice sheet topography and SMB–elevation feedback (as done for example in Gregory and Huybrechts, 2006, and Noël et al., 2021) is likely to result in an overestimation of the temperature threshold for ice sheet loss. Modelling studies including this mechanism (either explicitly or parameterised) estimated a global mean temperature (GMT) threshold for GrIS complete melt over the next millennia between 1.6 and 3 K above pre-industrial levels, with the rate of GrIS decline depending on the amount of warming above the threshold (Robinson et al., 2012; Levermann et al., 2013; Clark et al., 2016; Van Breedam et al., 2020; Gregory et al., 2020; Zeitz et al., 2022; Höning et al., 2023; Bochow et al., 2023). Paleo-data and modelling indicate that during the last interglacial period (LIG; ∼ 130–115 kyr BP), it is unlikely that the GMT exceeded 2 K above pre-industrial levels (Capron et al., 2014) and the GrIS contributed no more than 4 m to GMSL (Helsen et al., 2013; Goelzer et al., 2016; Plach et al., 2019; Sommers et al., 2021). This suggests that during the LIG the threshold for complete GrIS melt had not been passed or the warming had been too little or too short to induce a full GrIS collapse. Another possible paleo-analogue for 21st-century warming is the mid-Pliocene Warm Period (mPWP; ∼ 3.264–3.025 Myr BP; Haywood et al., 2011), which is estimated to have been 2–3 K warmer than pre-industrial levels. GrIS simulations for this period yield extremely variable ice sheet configurations, ranging from an ice-free state to a near-modern GrIS depending on the climate forcing selected (Dolan et al., 2015). Altogether, paleo- and future-ice-sheet modelling studies both suggest the existence of a threshold for GrIS complete melt in a warmer climate. However, there is still uncertainty in the nature of this threshold and whether or not the GrIS would exhibit a tipping-point behaviour once this threshold is passed. A recent study using an ice sheet model bi-directionally coupled to a low-resolution atmosphere global circulation model (GCM) found a gradual, almost linear decline in GrIS equilibrium mass in response to sustained global mean warming (Gregory et al., 2020), rather than the sharp threshold behaviour found in earlier work (Robinson et al., 2012; Levermann et al., 2013). A better understanding of the mechanisms regulating the GrIS response to sustained warming is needed to determine the existence of tipping points for GrIS complete ice sheet melt and as such reduce uncertainties in the GrIS long-term sea level rise (SLR).
Here, we explore a potential SMB threshold for complete melt of the GrIS; the impact and interplay of surface melt and GIA in determining this threshold; and whether the GrIS exhibits characteristics commonly associated with tipping points, such as sensitivity to external forcing. To this end, we force the higher-order Community Ice Sheet Model v.2 (CISM2; Lipscomb et al., 2019) with different SMB climatologies previously calculated with the full-complexity Community Earth System Model v.2 (CESM2; Danabasoglu et al., 2020) in a two-way coupled CESM2–CISM2 simulation of the global climate and GrIS (Muntjewerf et al., 2020b). The SMB calculation in CESM2 is based on a surface energy balance calculation and includes an advanced representation of snow–firn processes, such as snow compaction, refreezing, and surface albedo (Muntjewerf et al., 2021; Sellevold and Vizcaíno, 2020). In our simulations, the SMB forcing is updated as the GrIS surface elevation evolves through an elevation class calculation in the land component of CESM2 (Muntjewerf et al., 2021), while bedrock changes due to the GIA effect are accounted for in CISM2 through the elastic lithosphere–relaxing asthenosphere (ELRA) method (Le Meur and Huybrechts, 1996; Rutt et al., 2009).
The paper is structured as follows: in Sect. 2, we briefly describe CISM2 (Sect. 2.1), the SMB forcing (Sect. 2.2), and the experimental setup (Sect. 2.3). In Sect. 3 we analyse the main results, which are organised in four subsections on thresholds (Sect. 3.1), pattern and timescales (Sect. 3.2), processes (Sect. 3.3), and topographic control for GrIS complete melt (Sect. 3.4). In Sect. 4 we first discuss the thresholds found here in the context of the existing literature and end-of-century projections (Sect. 4.1) and the existence of a tipping point for GrIS decay (Sect. 4.2). We then draw our main conclusions and suggest possible future research directions (Sect. 4.3).
2.1 Ice sheet model description
CISM2 is a parallel, 3-D thermomechanical ice sheet model (ISM) which solves equations for the conservation of mass, momentum, and internal energy (Lipscomb et al., 2019). In this study, CISM2 solves a depth-integrated viscosity approximation of the Stokes equations for incompressible viscous flow (DIVA, Goldberg, 2011). At the horizontal resolution used in this study for the Greenland domain (4 km), DIVA outperformed other hybrid or zero-order solvers in terms of both model performance and representation of the ice-flow physics (Robinson et al., 2022). Basal sliding is calculated using a pseudo-plastic sliding law which incorporates linear, plastic, and power-law behaviour (Aschwanden et al., 2016). Ocean forcing at the marine-terminating outlet glaciers is not accounted here, and floating ice is immediately removed based on a simple flotation criterion. GIA is parameterised using the elastic lithosphere–relaxing asthenosphere (ELRA) model (see for example Rutt et al., 2009), which allows for taking account of a regional bedrock response to changes in ice load. The main CISM2 parameter values used in this study are provided in Table A1. Finally, while a more detailed description of all the CISM2 features and options can be found in Lipscomb et al. (2019), we highlight that the same model setup used here has previously been applied in two-way coupled simulations of the global climate and the GrIS over the next centuries (Muntjewerf et al., 2020b, a) as well as in the past (Sommers et al., 2021).
2.2 SMB forcing
Here, we provide a brief description of the general SMB calculation in CESM2 and how it is downscaled onto the CISM2 grid.
The SMB calculation is done in the land component of CESM2 (Community Land Model v5, CLM5; Lawrence et al., 2019) and is defined as
Snowfall is calculated from the total precipitation depending on the surface temperature (100 % snowfall if the temperature is below −2 °C, 100 % rain if the temperature is above 0 °C, and linear interpolation in between). Rainfall can contribute positively to the SMB if it refreezes within the snowpack. Snowmelt and ice melt are calculated based on the melt energy available within the ice column, which depends on the sum of net surface radiation, latent and sensible turbulent surface fluxes, and ground heat fluxes at the atmosphere–snow interface (Lawrence et al., 2019). In order to overcome the challenge of resolving steep SMB gradients around the ice sheet margins at relatively coarse typical CLM5 resolutions (1° in Muntjewerf et al., 2020b), the SMB is calculated at 10 elevation classes, with boundaries at 0, 200, 400, 700, 1000, 1300, 1600, 2000, 2500, 3000, and 10 000 m. This is done first by downscaling the CLM5 grid cell temperature to each elevation class using a uniform lapse rate of −6 K km−1. A vertically uniform relative humidity is then assumed to determine the potential temperature, specific humidity, air density, and surface pressure over each elevation class. The interpolated fields are then used to calculate the SMB components in each elevation class. After annual mean SMB is calculated at each elevation class in CLM5, it is then downscaled to the higher-resolution CISM2 domain through horizontal bilinear interpolation and linear vertical interpolation between adjacent elevation classes to the ice sheet model surface elevation. Remapping onto the CISM2 grid is followed by a normalisation step that guarantees conservation of SMB fluxes in both the accumulation and ablation zones. More details on the SMB calculation and on the CESM2–CISM2 coupling are also provided in Muntjewerf et al. (2021).
Table 1In the first four columns average values are shown from each of the 23-year-long intervals in the two-way coupled BG–1pct run used to force our simulations (transient global mean temperature anomaly to pre-industrial levels, transient GrIS temperature anomaly to pre-industrial levels, GrIS integrated initial SMB forcing, GrIS integrated initial SMB anomaly to pre-industrial levels). In the last two columns, the final GrIS volume (minimum/average/maximum, which are calculated within quasi-periodic oscillations) and time needed to reach the minimum GrIS volume in our simulations (i.e. time at which the GrIS retreat stops and quasi-periodic oscillations start) are shown. The average value is highlighted in bold. GrISMT: GrIS mean temperature.

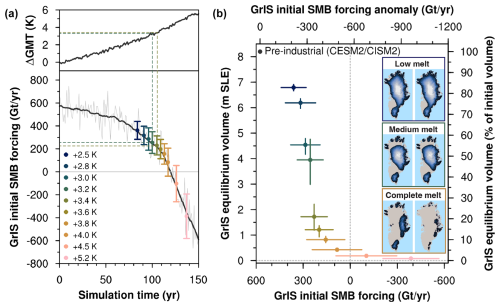
Figure 1(a) Time series of the (upper panel) global mean temperature (GMT) anomaly relative to pre-industrial levels and (bottom panel) GrIS integrated surface mass balance in the two-way coupled BG–1pct simulation (Muntjewerf et al., 2020b). In the bottom panel, the SMB forcing used in our simulations (avg ± SD) is indicated in different colours for each run (see the inset legend). Dashed lines highlight the transition between GrIS “medium melt” and “complete melt”. (b) Scatter plot of GrIS integrated initial SMB forcing (avg ± SD, x axis) vs. GrIS final volume (avg ± min/max, y axis). Avg, min, and max final volumes are calculated within quasi-periodic oscillations (see Sect. 3.3). Colours for each simulation as in the inset legend in (a). In the inset maps, the GrIS final extent is shown for two simulations belonging to each group (for the complete-melt group, +3.2 and +4.0 K runs are shown).
2.3 Experimental setup
In this study, we use a functionality of CESM2 that allows for running CISM2 within the Earth system model (ESM) architecture, forced with coupler history files of annual mean SMB calculated in previous CESM2 simulations at multiple elevation classes. Under this setup, each coupler history file contains annual mean SMB values at multiple elevation classes on the 1° land model (CLM5) grid in CESM2. During runtime, every year the CESM2 coupler selects an individual coupler history file and performs the trilinear (bilinear horizontal + linear vertical) interpolation of the annual mean SMB to the GrIS surface elevation on the CISM2 4 km grid, which is then followed by the normalisation step. In this way, the SMB is automatically updated during runtime for changes in ice sheet geometry, thus allowing us to account for the SMB–elevation feedback based on an advanced energy balance calculation accounting for snow–firn processes and energy fluxes at the ice sheet surface. We highlight that this setup allows for the use of SMB forcing files calculated in previous CESM2 simulations and as such changes in ice sheet geometry and melt are not feeding back on the climate (i.e. we keep CESM2 in data mode while using its coupler functionality). Our CISM2 simulations are forced with multiple-elevation-class SMB climatologies from a published, two-way coupled CESM2–CISM2 simulation of the global climate and GrIS under an idealised, high-greenhouse-gas (GHG) scenario (hereinafter referred to as BG–1pct run; Muntjewerf et al., 2020b). In this simulation, atmospheric CO2 concentration is increased by 1 % every year until it reaches 4 times pre-industrial values at year 140, after which it is kept fixed. From the BG–1pct run, we select several 23-year-long climatologies corresponding to different SMB and global mean temperature levels (values are shown in Table 1; see also Fig. 1a). The choice of each climatology being 23-year-long is the result of as a compromise between keeping the SMB standard deviation within the range of pre-industrial values and having a sampling rate large enough to prevent data aliasing. In each simulation, we cycle the 23-year-long, multiple-elevation-class SMB forcing for 80 kyr (or less if the ice sheet disappears earlier).
Each run is restarted from the BG–1pct run at the last year of the corresponding forcing interval (initial and final year of each forcing interval are shown in Table A2). This means that model parameter choices and the simulated GrIS thermodynamic memory rely on the spin-up of the coupled BG–1pct simulation, which is a two-way coupled CESM2–CISM2 pre-industrial equilibrium simulation of the global climate and GrIS described in Lofverstrom et al. (2020). In this spin-up, Lofverstrom et al. (2020) combine fully and partially coupled model configurations, running the (Greenland) ice sheet model component for 10 kyr. In the spin-up, the GrIS internal temperature was initialised with a 3-D temperature structure corresponding to the 9 kyr BP GrIS state in a full glacial cycle ice sheet model simulation (Fyke et al., 2014). This means that at the end of the spin-up simulation the GrIS internal temperature and rheology account for the thermal memory of the last glacial cycle. The ice sheet is free to evolve beyond its observed present-day extent throughout the 10 kyr of CISM2 simulation, and at the end of the spin-up procedure GrIS volume and area are overestimated by 12 % and 15 %, respectively, compared to present-day observations (Lofverstrom et al., 2020). During the spin-up procedure, model parameters (see Table A1) have been selected to best match present-day observations of ice extent, thickness, and velocity (Lofverstrom et al., 2020).
Table 2Comparison of GrIS integrated SMB (avg ± SD) for two-way coupled CESM2–CISM2 simulations and CESM2-only simulations for pre-industrial, historical, and available SSP scenarios contributing to CMIP6 (Coupled Model Intercomparison Project Phase 6). Note that in the CESM2-only runs the SMB is calculated and integrated over the prescribed, present-day observed GrIS elevation. Data from supporting information in Muntjewerf et al. (2020a).

In addition to the main simulations presented in this study, we performed several sensitivity simulations in which we do the following.
-
We switch off the GIA parameterisation in CISM2 to isolate the impact of GIA on the GrIS response to sustained warming.
-
We test different values for two model parameters in the GIA parameterisation: (i) characteristic mantle relaxation time and (ii) lithosphere flexural rigidity. The former determines the timing of the viscoelastic response of the asthenosphere (Cathles et al., 2023), whereas the latter embodies the lateral stiffness of the lithosphere (Walcott, 1970). For each parameter, we test lower- and higher-end values following previous work by Zweck and Huybrechts (2005) (see Table A1). With these sensitivity tests we aim to assess the dependence of the SMB thresholds and tipping behaviour of the GrIS on the selected GIA model parameters.
-
We prescribe lower values of the minimum friction angle in the pseudo-plastic sliding law (see Table A1). These sensitivity tests are aimed at assessing the impact of increasing sliding velocities (and, as a consequence, increased ice discharge) on the thresholds and tipping behaviour of the GrIS.
Here we first describe the relationship between SMB forcing and final GrIS volume to provide an SMB threshold for GrIS complete melt. We then illustrate the pattern and timescales for ice retreat, in particular for simulations close to the SMB threshold. We conclude by assessing the processes that determine the GrIS response to sustained warming.
3.1 Thresholds for GrIS complete melt
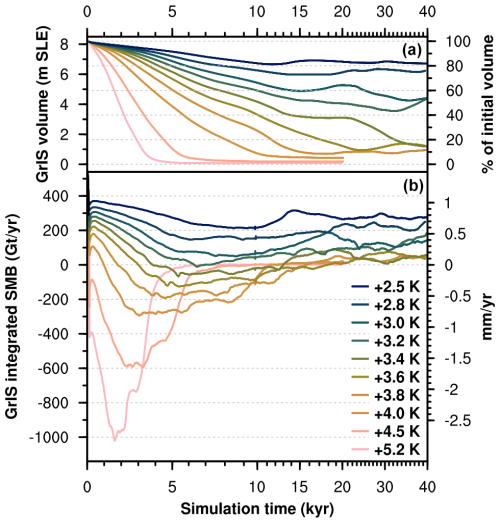
In our simulations, the GrIS exhibits a sharp threshold behaviour, with a nonlinear relationship between initial SMB forcing and GrIS melt/mass loss (Fig. 1b). In Table 1 we provide the values of initial SMB forcing, corresponding transient global mean and GrIS warming above pre-industrial levels, and resulting final GrIS volume for each simulation. Final GrIS states are clustered in three main groups: (a) “low melt”, i.e. less than 25 % GrIS mass loss; (b) “medium melt”, i.e. around 50 % GrIS mass loss; and (c) “complete melt”, i.e. more than 80 % GrIS mass loss. GrIS limited loss (< 25 %) is obtained for initial SMB forcing above 317 ± 97 Gt yr−1. Compared to the two-way coupled CESM2–CISM2 pre-industrial equilibrium simulation (hereafter BG–piControl run; Lofverstrom et al., 2020, 585 ± 85 Gt yr−1; see Table 2), this first SMB threshold for low melt corresponds to a decrease in the GrIS integrated SMB not exceeding 40 % and to a transient global mean warming below 2.8 K. An ice loss of around 50 % of the initial GrIS mass is obtained for an intermediate initial SMB forcing between 286 ± 94 and 255 ± 83 Gt yr−1 (between 40 % and 50 % decrease from the pre-industrial BG–piControl SMB), corresponding to global mean warming above pre-industrial levels between 2.8 and 3.4 K. Finally, we find that the GrIS is bound to completely melt if the initial SMB forcing is lower than 230 ± 84 Gt yr−1 (Fig. 1b and Table 1). This corresponds to a decrease of around 60 % of the GrIS integrated pre-industrial SMB at the end of the BG–piControl run. The SMB threshold for complete GrIS melt corresponds to, compared to the BG–piControl run, a transient global mean warming above pre-industrial levels of 3.4 K (Fig. 1a and Table 1).
3.2 Pattern and timescales of GrIS retreat
In the low-melt simulations, ice loss mostly takes place at the southwestern margin, with limited retreat in the north occurring in the +2.8 K run (see inset in Fig. 1b). The southwestern GrIS margin retreats all the way to the east in the medium-melt simulations, until a large ice cap on the southern tip of Greenland is disconnected from the GrIS main body. In these simulations, showing an intermediate GrIS loss, significant retreat also occurs in the north, whereas the midwestern ice sheet margin remains close to the coast (see inset in Fig. 1b). When the SMB threshold for complete GrIS melt is passed, the GrIS retreats all the way towards the east, with isolated ice caps of variable size remaining in regions of high bedrock elevation (see inset in Fig. 1b). The timescale needed to reach ice sheet deglaciation or stabilisation increases sharply as the initial SMB forcing gets close to the threshold for GrIS complete mass loss. In the low-melt simulations, minimum GrIS volume is reached within the first 15 kyr (Fig. 2 and Table 1). Timescales are doubled for the medium-melt simulations, in which the GrIS attains minimum volume after around 30–35 kyr. The simulation immediately above the SMB threshold (+3.4 K run) shows the longest response time, as the GrIS keeps decreasing until 40 kyr, after a retreat slowdown between 15 and 20 kyr (Fig. 2 and Table 1). For the other simulations in the complete-melt group, timescales decrease quickly as the initial SMB forcing gets lower and moves away from the threshold. For positive initial SMB forcing, the shortest GrIS deglaciation time is around 12 kyr, whereas if the initial SMB forcing is negative, Greenland becomes mostly ice-free in 8 kyr or fewer (Fig. 2). A detailed GrIS retreat pattern and timescales for each simulation are displayed in the supplementary videos.
3.3 Processes controlling ice retreat
In our simulations, the response of the GrIS to sustained warming is primarily determined by the interplay of surface melt and GIA, which are interconnected through SMB–elevation feedback. For every initial SMB forcing level, the ice sheet loses mass during the first 10–15 kyr and the SMB further decreases due to ice thinning and surface elevation lowering (Fig. 2). However, the impact of ice thinning is mitigated and, in some cases, counterbalanced by GIA: while the ice sheet thins and retreats, the bedrock uplifts, thus increasing the surface elevation and, consequently, the SMB (see the bottom panel in Fig. 2 and supplementary videos, for instance the video showing the +3.2 and 3.4 K runs). This interplay is key in determining whether the ice sheet will disappear or not: GrIS complete loss is achieved only in simulations where the surface lowering outweighs the bedrock uplift and the SMB becomes and remains negative for at least a few thousand years (Fig. 2). When this does not happen, the GrIS eventually reaches a stable configuration as in the low-melt or medium-melt groups. In the simulations that are closest to the threshold for complete GrIS melt, the interplay of SMB–elevation feedback and GIA also causes self-sustained, quasi-periodic ice sheet oscillations ranging from 3 % to 12 % of the initial GrIS mass. In fact, in some cases the increase in SMB due to GIA-induced bedrock uplift can promote ice thickening and margin readvance. This mechanism is then reverted when the isostatic subsidence resulting from ice thickening causes the SMB to decrease again, which is enough to promote ice thinning and margin retreat (see supplementary videos of the +3.0, +3.2, and +3.4 runs). The amplitude and periodicity of these oscillations increase as the initial SMB forcing gets closer to the threshold for complete GrIS melt. The highest oscillation amplitude and periodicity is obtained in the simulation immediately after the SMB threshold is crossed (+3.2 K run, with a volume oscillations of 12 % of the initial ice mass and over cycles of 30 kyr; see Fig. A1).
If GIA is switched off, the response of the GrIS changes drastically, as shown in Figs. 3 and 4. When we turn off GIA for a simulation in the low-melt group (+2.5 K run), SMB–elevation feedback due to surface lowering causes the GrIS to deglaciate in 20 kyr (Fig. 3). This is equivalent, both in terms of final GrIS mass and timing response, to a simulation in the complete-melt group, with initial SMB forcing above the threshold for GrIS complete melt (+3.6 K run; see Fig. 2). For other simulations in the medium-melt or complete-melt group, removing the GIA effect results in rapid GrIS deglaciation in around 10 kyr or less (Fig. 3). We find that, when GIA is not accounted for, complete GrIS melt is achieved for initial SMB forcing of 488 ± 91 Gt yr−1, which is twice as high as when GIA is included and corresponds to a global mean warming above pre-industrial levels of 1.6 K. Without GIA, the GrIS threshold behaviour is also exacerbated, with the final GrIS state switching directly from low melt to complete melt (Fig. 4). The primary role played by GIA in determining the SMB threshold and response of the GrIS to sustained warming also emerges in sensitivity tests repeating the first simulation after the SMB threshold is passed (+3.4 K run) under lower- and higher-end values for model parameters in the GIA parameterisation (characteristic mantle relaxation time and lithosphere flexural rigidity; see Sect. 2.3 and Table A1). While in these sensitivity experiments the GrIS loses more than 80 % of its initial mass for all the parameter values explored, timescales to reach minimum ice sheet volume, as well as the timing and strength of GIA-induced oscillation, vary considerably (Fig. 5). In particular, for a low mantle relaxation time, GrIS deglaciation is slower and more gradual. For a high value of the characteristic mantle relaxation time, the GrIS deglaciates faster (around 15 kyr) and the ice volume remains low until 50 kyr. However, after that time the GrIS regrows up to 40 % of its initial volume. A similar late regrowth is also observed for a low value of the lithosphere flexural rigidity, although in this case minimum GrIS volume is reached much later between 60 and 70 kyr.
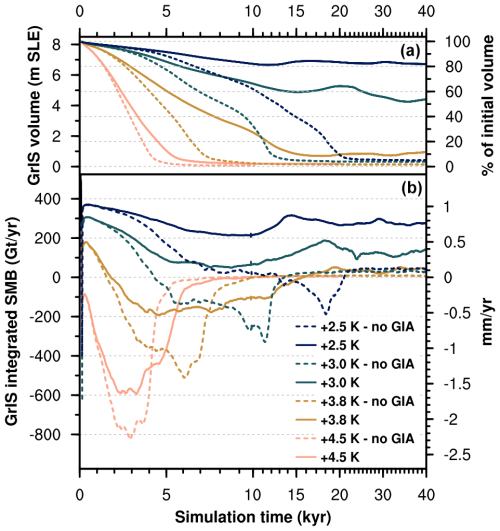
Figure 3Time series of (a) GrIS volume and (b) integrated surface mass balance for selected sensitivity simulations with GIA turned on (solid lines) and GIA turned off (dashed lines). Note that simulation time on the x axis is irregular (minor tick marks every 1000 years).
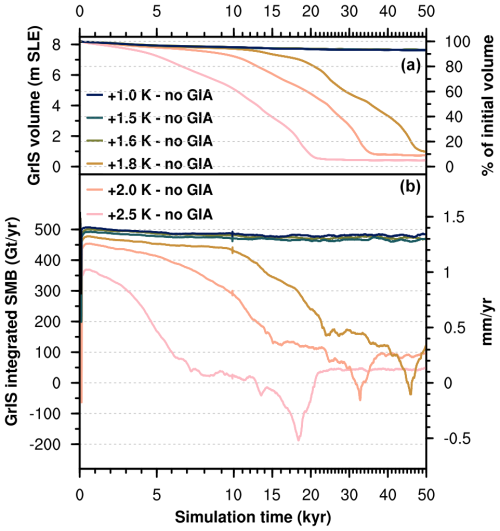
Figure 4Time series of (a) GrIS volume and (b) integrated surface mass balance for selected sensitivity simulations with GIA turned off. Note that simulation time on the x axis is irregular (minor tick marks every 1000 years).
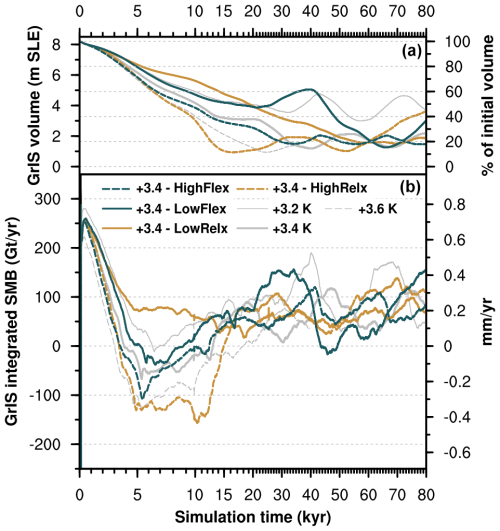
Figure 5Time series of (a) GrIS volume and (b) integrated surface mass balance for selected sensitivity simulations with different GIA parameters. LowRelx (HighRelx): low (high) values of the characteristic mantle relaxation time; LowFlex (HighFlex): low (high) values of the flexural rigidity of the lithosphere. Values are shown in Table A2. Note that simulation time on the x axis is irregular (minor tick marks every 1000 years).
Finally, we tested the impact of increased ice discharge on the long-term GrIS evolution. As we do not account for ocean forcing at the marine-terminating outlet glacier, we triggered in our sensitivity simulations an increase in ice discharge by prescribing lower values of the minimum friction angle in the pseudo-plastic sliding law (see Sect. 2.3). In particular, we repeated the simulation immediately below the SMB threshold for complete GrIS melt (+3.2 K), imposing an extremely low friction angle value (0.5°; see dashed green curve in Fig. A3). In this sensitivity test, we immediately observe an increase in ice discharge due to higher sliding velocities, and after 500 years in the simulation the total GrIS mass budget is the same as in the 3.8 K run (which is well above the SMB threshold; see Fig. 2). Nevertheless, the long-term evolution of the +3.2 K simulation under increased sliding is almost identical to the reference case, with a final GrIS volume of around 50 % of its pre-industrial value. This shows that in our simulations the GrIS long-term response to sustained warming and the SMB threshold for complete GrIS melt are dominated by surface processes.
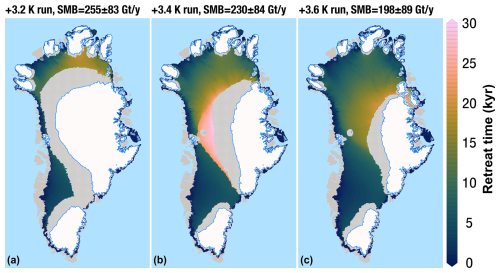
Figure 6Map of GrIS retreat time for the (a) +3.2 K run, (b) +3.4 K run, and (c) +3.6 K run. Ice sheet areas showing GIA-induced margin oscillations are shown in grey, whereas continuously ice-covered areas throughout each run are white.
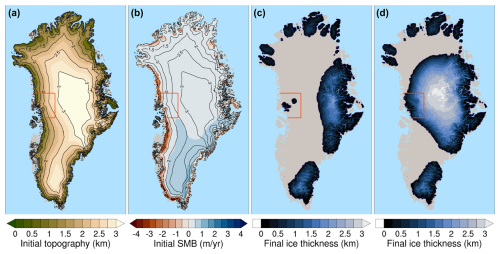
Figure 7Map of the (a) GrIS surface topography at the beginning of our simulations, (b) GrIS initial SMB forcing for the +3.4 K run, (c) GrIS final volume for the +3.4 K run, and (d) GrIS final volume for the +3.4 K run with constant SMB (i.e. no SMB–elevation feedback) in the central western coastal region (i.e. inside the red box shown in each panel).
3.4 Topographic control on GrIS complete melt
A comparison of the simulations immediately below and above the SMB threshold for GrIS complete melt (+3.2 and +3.4 K runs, respectively) indicates that the ice margin position in the central west is crucial to determining the final ice sheet state. When the GrIS central western margin remains sufficiently close to a coastal region with relatively high topography and SMB (indicated by the red box in Fig. 7), possibly reestablishing a connection during margin readvances within self-sustained oscillations, the ice loss in the southwest and north remains limited (see +3.2 K run in Fig. 6 and the related supplementary video). When instead the midwestern margin permanently loses contact with this coastal region, the GrIS retreats towards the east and loses more than 80 % of its mass (see the +3.4 K run in Fig. 6 and related supplementary video). In the first simulation above the SMB threshold, the central western margin starts to retreat towards the east only after 20 kyr, when the connection between the ice sheet and the high-topography coastal region is permanently lost. In the remaining simulations after the SMB threshold is crossed (+3.6, +3.8, +4.0, +4.5, +5.2 K), the connection between the central western margin and the coastal region with high topography is lost earlier (around 15 kyr or sooner) and the retreat pattern is more uniform in time (see the right panel in Fig. 6 and related supplementary videos). To further test the role played by the surface topography in the central west on the GrIS abrupt retreat, we repeated the first simulation above the SMB threshold (+3.4 K run) while keeping the SMB fixed (i.e. inhibiting the SMB–elevation feedback) in the high-topography coastal region (i.e. inside the red box in Fig. 7). When we impose this (local) additional constraint, nearly complete mass loss of the GrIS is prevented, with a final ice sheet extent (right panel in Fig. 7) and volume (Fig. 8) almost identical to those of the simulation immediately below the SMB threshold (+3.2 K run). GrIS complete loss is also prevented when we apply the same local SMB–elevation feedback constraint to the +3.6 K simulation (in which the GrIS is deglaciating in 20 kyr), whereas for higher forcings, GrIS loss cannot be prevented. Overall, our simulations show that the relatively confined central western coastal region has a stabilising effect on the GrIS response to sustained warming and, as such, plays a primary role in determining whether the ice sheet will or will not pass the threshold towards complete melt.
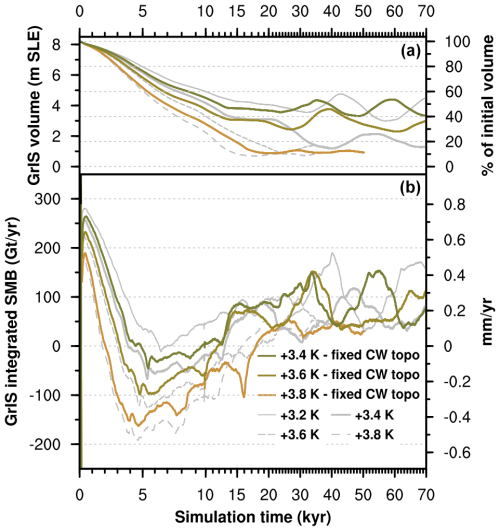
Figure 8Time series of (a) GrIS volume and (b) integrated surface mass balance for selected sensitivity simulations with constant SMB (i.e. no SMB–elevation feedback) in the central western coastal region (i.e. inside the red box in Fig. 7). Sensitivity simulations are labelled with “fixed CW topo” (central western). Note that simulation time on the x axis is irregular (minor tick marks every 1000 years).
In this section, we first compare the thresholds found here with the existing literature and we analyse these thresholds in the context of end-of-century projections. Then, we examine the behaviour of the GrIS with a specific focus on the potential tipping point associated with the SMB threshold for complete melt. While we discuss the GrIS response to sustained melt, the nonlinear and abrupt nature of those responses, and the sensitivity to external factors, it is important to reiterate here that our primary objective is to explore the SMB threshold itself, rather than the aspects of multistability or reversibility often associated with tipping points.
4.1 Thresholds for complete GrIS melt
Here we have found a positive SMB threshold of 230 ± 84 Gt yr−1 for complete GrIS melt. This corresponds to a 60 % decrease from the GrIS pre-industrial SMB calculated in a two-way coupled CESM2–CISM2 equilibrium simulation (585 ± 83 Gt yr−1; see Table 2 and Lofverstrom et al., 2020). In this pre-industrial two-way coupled ESM–ISM simulation no corrections are applied to the SMB (e.g. SMB masking outside the present-day GrIS extent) and the GrIS is left free to evolve. Although CESM2 compares reasonably well with ERA-Interim and RACMO2 for several key controls on the SMB over Greenland (surface melt, runoff, longwave radiation, van Kampenhout et al., 2020; Noël et al., 2020), this approach led to an overestimation of the GrIS initial extent (15 %) and volume (13 %) and, as a consequence, to an integrated SMB over the GrIS which is higher than in uncoupled CESM2 experiments of the historical period (390 ± 28 Gt yr−1; see Table 2 and Lofverstrom et al., 2020) and recent satellite observations (437 ± 17 Gt yr−1, Mouginot et al., 2019). In view of this, the positive SMB threshold found here is coupled model dependent and remains complicated regarding analysing the context of end-of-century projections or making a direct comparison with other modelling studies and recent observations. Constraining ISM simulations to GrIS changes during the LIG, Robinson et al. (2012) found a positive SMB threshold for complete ice sheet melt ranging between 150–340 Gt yr−1. This agrees reasonably well with our study, although in Robinson et al. (2012) the pre-industrial SMB is lower (around 400 Gt yr−1). In the two-way coupled CESM2–CISM2 projection for the SSP5-8.5 scenario, the SMB crosses our threshold for GrIS instability between years 2060–2080 and by the end of the century it becomes negative (Muntjewerf et al., 2020a). In our simulations, negative SMB forcing leads to relatively rapid GrIS deglaciation in less than 10 kyr (Table 1 and Fig. 2). While coupled CESM2–CISM2 simulations for lower-emission scenarios (SSP1-2.6, SSP2-4.5, SSP3-7.0) are currently not available, in the corresponding CESM2-only future projections the SMB over the GrIS at the end of the century is well below the threshold found here, regardless of the emission scenario considered (see Table 2). This comparison, however, must be considered carefully as (a) the GrIS pre-industrial SMB is lower in CESM2-only runs and (b) in CESM2-only runs, the SMB is calculated over a fixed present-day GrIS topography, and as such the SMB–elevation feedback is not accounted for.
The SMB threshold found here corresponds to a transient global mean and GrIS warming of 3.4 and 3.2 K above pre-industrial levels, respectively. Our global mean warming threshold is at the high end of previous ice sheet modelling studies with climate forcing (a) calculated offline with GCMs (3.1 K, Gregory and Huybrechts, 2006) and (b) interactively calculated with regional models or an intermediate-complexity ESM (1.6–3 K, Robinson et al., 2012; Levermann et al., 2013; Gregory and Huybrechts, 2006; Höning et al., 2023). We highlight however that in our forcing method the SMB has not fully equilibrated with the climate and more sustained warming of 3.4 K above pre-industrial levels would likely result in a lower SMB as the snowpack deteriorates (ablation area expansion, less refreezing capacity). To properly determine a global mean warming threshold for complete GrIS melt would require running further CESM2–CISM2 assessments fully or asynchronously coupled experiments, which is computationally too expensive and out of the scope of this study.
4.2 GrIS tipping-point behaviour
Our simulations indicate that the GrIS response to sustained warming is nonlinear and that the ice sheet is tipping from 50 % mass towards complete melt once the positive SMB threshold is passed. This agrees well with early modelling studies (Gregory and Huybrechts, 2006; Robinson et al., 2012; Levermann et al., 2013). However, our results do not agree with those of Gregory et al. (2020), which suggest a gradual, almost linear GrIS decline in response to sustained warming. In their study, Gregory et al. (2020) used an ISM bi-directionally coupled to a low-resolution atmosphere GCM and used elevation classes to downscale the SMB onto the ice sheet model grid. While in our simulations we also use elevation classes to downscale the SMB forcing onto the CISM2 grid, GrIS changes are not communicated back to CESM2, and as such we do not account for a number of ice–atmosphere feedbacks (e.g. increased cloudiness and snowfall as the ice sheet margin moves towards the interior). In Gregory et al. (2020), these processes result in an increase in precipitation which in some cases counterbalances the effect of the SMB–elevation feedback and leads to the multiple stable GrIS states. However, in our simulations the GrIS tipping behaviour is determined by the interplay of SMB–elevation feedback and GIA, with the latter not being accounted for in Gregory et al. (2020). While we cannot rule out that accounting for ice–atmosphere feedbacks would stabilise the GrIS and change the SMB threshold, it is also difficult to determine if they would drastically change the nonlinear nature of the GrIS response to sustained warming found here. Another recent study by Zeitz et al. (2022) found a similar, nonlinear impact of the interplay between GIA and SMB–elevation on the GrIS response to sustained warming, with final GrIS states clustered in three main groups for a global warming exceeding 2 K above pre-industrial levels (“partial recovery”, “oscillations”, “loss”). Zeitz et al. (2022) used a different ISM and GIA parameterisation than that in our study, thus suggesting that the GrIS tipping behaviour simulated here is unlikely to depend on our model setup. Our study also agrees well with Zeitz et al. (2022) and Plach et al. (2019) in showing that increased ice discharge rates have no effect on the long-term GrIS equilibrium response to sustained warming.
We find that the GrIS is tipping towards complete melt if the ice margin in the central west retreats enough to disconnect from a group of isolated ice caps with high bedrock elevation and SMB. If the ice margin remains pinned to this topographic pinning point, GrIS loss is also limited in southwestern and northern Greenland and does not exceed 50 % of the initial GrIS mass. The presence of this topographic feature of the GrIS, in combination with a stable midwestern margin position and limited ice loss in the southwest and north, has consistently been simulated in ice sheet modelling studies of the LIG (Helsen et al., 2013; Plach et al., 2019; Goelzer et al., 2016; Sommers et al., 2021). In these simulations, the midwestern margin remains pinned to the topographic pinning point and the GrIS does not lose more than 4 m SLE. In particular, in a recently published two-way coupled CESM2–CISM2 simulation of the global climate and GrIS during the LIG, the ice sheet extent 123 kyr ago is very similar to those in our simulations belonging to the medium-melt group (see Fig. 3 in Sommers et al., 2021). After this time, however, the SMB becomes positive and the GrIS starts to readvance towards the west. This suggests that around 123 kyr ago the GrIS might have been close to tipping towards a much reduced state. Compared with other modelling studies indicating GrIS tipping-point behaviour in response to sustained warming, our study agrees by showing that the ice sheet retreats towards the east and that the midwestern margin remains close to the coast before tipping (Robinson et al., 2012; Höning et al., 2023; Zeitz et al., 2022).
4.3 Conclusions and future research
Here, we have used a state-of-the-art, higher-order ice sheet model (CISM2) to (1) determine a SMB threshold for GrIS complete melt, (2) investigate the nature of this threshold, and (3) understand the processes controlling the ice sheet response. We forced CISM2 with different levels of SMB, having been previously calculated at multiple elevation classes with a full-complexity Earth system model (CEMS2) which includes an advanced representation of snow–firn processes, surface albedo, and melt. In our simulations, the SMB is updated as the ice sheet surface elevation changes through the elevation class method. This allows us to account for the SMB–elevation feedback during GrIS lowering and retreat. Bedrock changes due to GIA effects are accounted for in CISM2 through the ELRA parameterisation.
We have found a positive SMB threshold for complete GrIS melt of 230 ± 84 Gt yr−1, corresponding to a 60 % decrease from the GrIS pre-industrial equilibrium SMB. This SMB threshold corresponds to a transient global mean and GrIS warming of 3.4 and 3.2 K above pre-industrial levels, respectively. The thresholds found here are in overall agreement with previous studies. In our simulations, the response of GrIS to sustained warming is nonlinear and final ice sheet state are clustered in three main groups: (a) low melt (< 25 % mass loss), (b) medium melt (∼ 50 % mass loss), and (c) complete melt (> 80 % mass loss). This tipping behaviour is determined by the effect of SMB–elevation feedback in response to surface melt and GIA. While topographic lowering due to surface melt promotes further melt and ice loss, GIA causes a bedrock uplift which in turn yields reduced melt, ice thickening, and margin stabilisation or readvance. The GrIS tips from ∼ 50 % mass towards complete loss when the melt-induced surface lowering outweighs the GIA-induced bedrock uplift, and the initially positive SMB becomes and remains negative for at least a few thousand years. Similar tipping behaviour of the GrIS, resulting from the interplay of SMB–elevation feedback and GIA, has also been recently simulated by Zeitz et al. (2022) using a different ISM and GIA parameterisation. However, recent two-way coupled modelling work suggests that ice–atmosphere negative feedbacks which are not accounted for in our simulations might dampen the nonlinear response of the GrIS to sustained warming (Gregory et al., 2020). We have found that whether the GrIS will tip towards complete melt or not depends on the ice sheet margin position in the central west. When the ice margin remains close/connected to a coastal region with high bedrock elevation and SMB, GrIS loss is also limited in the southwest and north and does not exceed ∼ 50 % of its initial volume. Previous modelling studies of the GrIS during the LIG show that the ice sheet had, at its minimum extent, a configuration similar to that in our simulations in the medium-melt group. In view of this, we suggest that the central western high-topography coastal region might have played a stabilising role similar to that of the GrIS evolution during the LIG. The modelling approach presented here includes an advanced representation of the SMB–elevation and albedo feedback through the CESM2 melt energy calculation, snow–firn model, and elevation class approach. Nevertheless, the main caveat of this study is that CISM2 is not bi-directionally coupled to CESM2, and as such we do not account for a number of ice sheet–atmosphere feedbacks (e.g. increase in cloud cover and precipitation as the GrIS retreats towards the interior). Moreover, there are uncertainties arising from the elevation class approach which is at the core of our SMB forcing method. In CESM2, the air temperature is downscaled to each elevation class using a constant lapse rate of 6 K km−1. While Sellevold et al. (2019) demonstrated that this value yields realistic SMB gradients over the GrIS, air temperature lapse rate values can show relatively large variations depending on conditions at the ice surface, seasonality, or even the background climate (Erokhina et al., 2017). The specific simulation setup used in this study, however, does not allow for exploring the impact of different lapse rate values, as the SMB at multiple elevation classes was previously calculated in a fully coupled CESM2–CISM2 simulation (Muntjewerf et al., 2020b) and is used in this study as a forcing file only. Finally, our sensitivity experiments show that the GrIS response to sustained warming might vary under different, physically realistic values of GIA parameters, especially in terms of timescales. Although widely used in ice sheet model simulations, the GIA parameterisation used in our study is relatively simple and does not account for lateral variations in the lithospheric thickness and upper-mantle viscosity. To better understand the nature of the response of the GrIS to sustained warming, further ice sheet–climate–solid-Earth coupled modelling efforts should be dedicated to fully or better resolve the interplay of ice–atmosphere feedbacks and GIA. In addition, future modelling studies of the GrIS during the LIG could shed light on how close the GrIS might have been to tipping at its minimum extent and which processes might have prevented that.
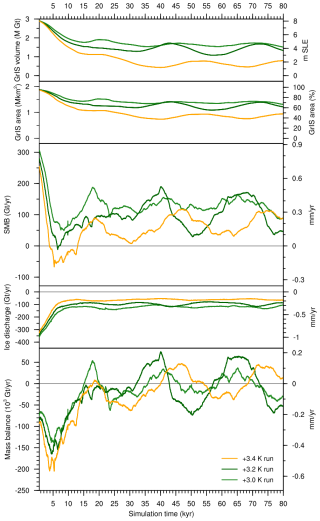
Figure A1Time series of GrIS volume, area, surface mass balance, ice discharge, and mass balance for selected simulations extended until 80 kyr to show the quasi-periodicity of GIA-induced oscillations.
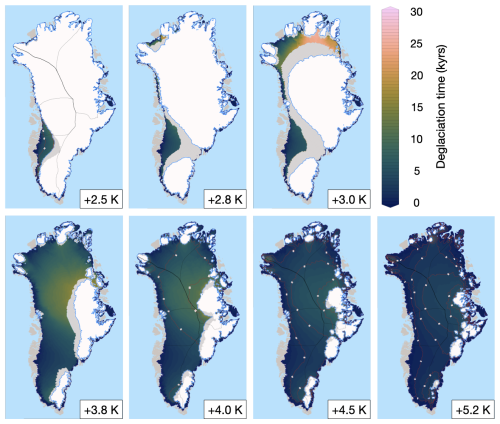
Figure A2Map of GrIS retreat time for the simulations not shown in Fig. 6. Ice sheet areas showing GIA-induced margin oscillations are shown in grey, whereas continuously ice-covered areas throughout each run are white.
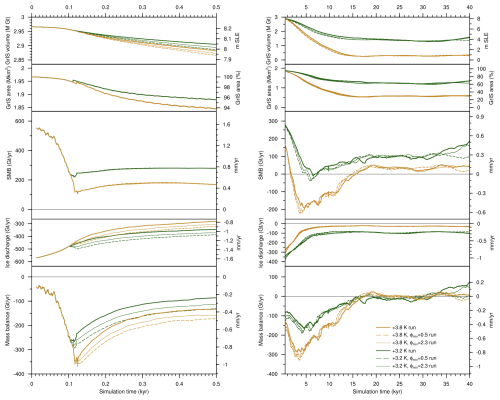
Figure A3Time series of GrIS volume, area, surface mass balance, ice discharge, and mass balance for selected sensitivity simulations with increased ice discharge through a reduced minimum friction angle in the pseudo-plastic sliding law (thick solid line: ϕmin = 5, thin solid line: ϕmin = 2.3, dashed line: ϕmin = 0.5. On the left, values between in the first 500 years are shown. On the right, values between 500 and 40 000 years are shown.
Table A1Model parameters used in the main CISM2 simulations presented in this study. Parameter values tested in sensitivity simulations are indicated in brackets.

CESM2 is an open-source model, available at https://www.cesm.ucar.edu/models/cesm2 (NSF NCAR, 2024) and https://github.com/ESCOMP/CESM/tree/release-cesm2.1.5 (last access: 2 April 2020). Computing and data storage resources, including the Cheyenne supercomputer (https://doi.org/10.5065/D6RX99HX Computational and Information Systems Laboratory, 2019), were provided by the Computational and Information Systems Laboratory (CISL) at the National Science Foundation (NSF) National Center for Atmospheric Research (NCAR). Forcing files from the two-way coupled CESM2–CISM2 simulations and setup scripts to reproduce our simulations are stored in the Cheyenne supercomputer and available upon request.
Supplementary videos can be found on Zenodo (https://doi.org/10.5281/zenodo.8384527, Petrini, 2023).
MV planned the research. MS performed an initial set of simulations. MP performed the remaining simulations, analysed the output, and wrote the manuscript. All authors discussed the results and reviewed and edited the manuscript.
The contact author has declared that none of the authors has any competing interests.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims made in the text, published maps, institutional affiliations, or any other geographical representation in this paper. While Copernicus Publications makes every effort to include appropriate place names, the final responsibility lies with the authors.
The CESM project is supported primarily by the National Science Foundation (NSF). This material is based upon work supported by the National Center for Atmospheric Research, which is a major facility sponsored by the NSF (cooperative agreement no. 1852977). Michele Petrini, Miren Vizcaino, Laura Muntjewerf, and Raymond Sellevold received funding from the European Research Council (grant no. ERC-StG-678145-CoupledIceClim). Michele Petrini and Heiko Goelzer have received funding from the Research Council of Norway (project no. 324639). Storage resources were provided by Sigma2 – the National Infrastructure for High Performance Computing and Data Storage in Norway (project no. NS8006K). In this paper, we used colour schemes from Crameri (2018) to prevent visual distortion of the data and exclusion of readers with colour-vision deficiencies (Crameri et al., 2020).
This research has been supported by the European Research Council H2020 programme (grant no. 678145).
This paper was edited by Ruth Mottram and reviewed by three anonymous referees.
Aschwanden, A., Fahnestock, M. A., and Truffer, M.: Complex Greenland outlet glacier flow captured, Nat. Commun., 7, 10524, https://doi.org/10.1038/ncomms10524, 2016. a
Bochow, N., Poltronieri, A., Robinson, A., Montoya, M., Rypdal, M., and Boers, N.: Overshooting the critical threshold for the Greenland ice sheet, Nature, 622, 528–536, 2023. a
Box, J. E., Fettweis, X., Stroeve, J. C., Tedesco, M., Hall, D. K., and Steffen, K.: Greenland ice sheet albedo feedback: thermodynamics and atmospheric drivers, The Cryosphere, 6, 821–839, https://doi.org/10.5194/tc-6-821-2012, 2012. a
Capron, E., Govin, A., Stone, E. J., Masson-Delmotte, V., Mulitza, S., Otto-Bliesner, B., Rasmussen, T. L., Sime, L. C., Waelbroeck, C., and Wolff, E. W.: Temporal and spatial structure of multi-millennial temperature changes at high latitudes during the Last Interglacial, Quaternary Sci. Rev., 103, 116–133, 2014. a
Cathles, L., Fjeldskar, W., Lenardic, A., Romanowicz, B., Seales, J., and Richards, M.: Influence of the asthenosphere on earth dynamics and evolution, Sci. Rep., 13, 13367, https://doi.org/10.1038/s41598-023-39973-y, 2023. a
Clark, P. U., Shakun, J. D., Marcott, S. A., Mix, A. C., Eby, M., Kulp, S., Levermann, A., Milne, G. A., Pfister, P. L., Santer, B. D., Daniel P. Schrag, Solomon, S., Stocker, T. F., Strauss, B. H., Weaver, A. J., Winkelmann, R., Archer, D., Bard, E., Goldner, A., Lambeck, K., Pierrehumbert, R. T., and Plattner, G.-K.: Consequences of twenty-first-century policy for multi-millennial climate and sea-level change, Nat. Clim. Change, 6, 360–369, 2016. a
Computational and Information Systems Laboratory: Cheyenne: HPE/SGI ICE XA System (Climate Simulation Laboratory), National Center for Atmospheric Research, Boulder, CO, https://doi.org/10.5065/D6RX99HX, 2019. a
Crameri, F.: Scientific colour maps, Zenodo [code], https://doi.org/10.5281/zenodo.5501399, 2018. a
Crameri, F., Shephard, G. E., and Heron, P. J.: The misuse of colour in science communication, Nat. Commun., 11, 5444, https://doi.org/10.1038/s41467-020-19160-7, 2020. a
Danabasoglu, G., Lamarque, J.-F., Bacmeister, J., Bailey, D. A., DuVivier, A. K., Edwards, J., Emmons, L. K., Fasullo, J., Garcia, R., Gettelman, A., Hannay, C., Holland, M. M., Large, W. G., Lauritzen, P. H., Lawrence, D. M., Lenaerts, J. T. M., Lindsay, K., Lipscomb, W. H., Mills, M. J., Neale, R., Oleson, K. W., Otto-Bliesner, B., Phillips, A. S., Sacks, W., Tilmes, S., van Kampenhout, L., Vertenstein, M., Bertini, A., Dennis, J., Deser, C., Fischer, C., Fox-Kemper, B., Kay, J. E., Kinnison, D., Kushner, P. J., Larson, V. E., Long, M. C., Mickelson, S., Moore, J. K., Nienhouse, E., Polvani, L., Rasch, P. J., and Strand, W. G.: The community earth system model version 2 (CESM2), Journal of Advances in Modeling Earth Systems, 12, e2019MS001916, https://doi.org/10.1029/2019MS001916, 2020. a
Dolan, A. M., Hunter, S. J., Hill, D. J., Haywood, A. M., Koenig, S. J., Otto-Bliesner, B. L., Abe-Ouchi, A., Bragg, F., Chan, W.-L., Chandler, M. A., Contoux, C., Jost, A., Kamae, Y., Lohmann, G., Lunt, D. J., Ramstein, G., Rosenbloom, N. A., Sohl, L., Stepanek, C., Ueda, H., Yan, Q., and Zhang, Z.: Using results from the PlioMIP ensemble to investigate the Greenland Ice Sheet during the mid-Pliocene Warm Period, Clim. Past, 11, 403–424, https://doi.org/10.5194/cp-11-403-2015, 2015. a
Erokhina, O., Rogozhina, I., Prange, M., Bakker, P., Bernales, J., Paul, A., and Schulz, M.: Dependence of slope lapse rate over the Greenland ice sheet on background climate, J. Glaciol., 63, 568–572, 2017. a
Fettweis, X., Franco, B., Tedesco, M., van Angelen, J. H., Lenaerts, J. T. M., van den Broeke, M. R., and Gallée, H.: Estimating the Greenland ice sheet surface mass balance contribution to future sea level rise using the regional atmospheric climate model MAR, The Cryosphere, 7, 469–489, https://doi.org/10.5194/tc-7-469-2013, 2013. a
Fox-Kemper, B., Hewitt, H., Xiao, C., Aðalgeirsdóttir, G., Drijfhout, S., Edwards, T., Golledge, N., Hemer, M., Kopp, R., Krinner, G., Mix, A., Notz, D., Nowicki, S., Nurhati, I., Ruiz, L., Sallée, J.-B., Slangen, A., and Yu, Y.: Ocean, Cryosphere and Sea Level Change, Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA, 1211–1362, https://doi.org/10.1017/9781009157896.011, 2021. a
Fürst, J. J., Goelzer, H., and Huybrechts, P.: Ice-dynamic projections of the Greenland ice sheet in response to atmospheric and oceanic warming, The Cryosphere, 9, 1039–1062, https://doi.org/10.5194/tc-9-1039-2015, 2015. a
Fyke, J., Sergienko, O., Löfverström, M., Price, S., and Lenaerts, J. T.: An overview of interactions and feedbacks between ice sheets and the Earth system, Rev. Geophys., 56, 361–408, 2018. a
Fyke, J. G., Sacks, W. J., and Lipscomb, W. H.: A technique for generating consistent ice sheet initial conditions for coupled ice sheet/climate models, Geosci. Model Dev., 7, 1183–1195, https://doi.org/10.5194/gmd-7-1183-2014, 2014. a
Goelzer, H., Huybrechts, P., Loutre, M.-F., and Fichefet, T.: Last Interglacial climate and sea-level evolution from a coupled ice sheet–climate model, Clim. Past, 12, 2195–2213, https://doi.org/10.5194/cp-12-2195-2016, 2016. a, b, c
Goelzer, H., Nowicki, S., Payne, A., Larour, E., Seroussi, H., Lipscomb, W. H., Gregory, J., Abe-Ouchi, A., Shepherd, A., Simon, E., Agosta, C., Alexander, P., Aschwanden, A., Barthel, A., Calov, R., Chambers, C., Choi, Y., Cuzzone, J., Dumas, C., Edwards, T., Felikson, D., Fettweis, X., Golledge, N. R., Greve, R., Humbert, A., Huybrechts, P., Le clec'h, S., Lee, V., Leguy, G., Little, C., Lowry, D. P., Morlighem, M., Nias, I., Quiquet, A., Rückamp, M., Schlegel, N.-J., Slater, D. A., Smith, R. S., Straneo, F., Tarasov, L., van de Wal, R., and van den Broeke, M.: The future sea-level contribution of the Greenland ice sheet: a multi-model ensemble study of ISMIP6, The Cryosphere, 14, 3071–3096, https://doi.org/10.5194/tc-14-3071-2020, 2020. a
Goldberg, D. N.: A variationally derived, depth-integrated approximation to a higher-order glaciological flow model, J. Glaciol., 57, 157–170, 2011. a
Gregory, J. and Huybrechts, P.: Ice-sheet contributions to future sea-level change, Philos. T. R. Soc. A, 364, 1709–1732, 2006. a, b, c, d
Gregory, J. M., George, S. E., and Smith, R. S.: Large and irreversible future decline of the Greenland ice sheet, The Cryosphere, 14, 4299–4322, https://doi.org/10.5194/tc-14-4299-2020, 2020. a, b, c, d, e, f, g, h, i, j
Haywood, A. M., Dowsett, H. J., Robinson, M. M., Stoll, D. K., Dolan, A. M., Lunt, D. J., Otto-Bliesner, B., and Chandler, M. A.: Pliocene Model Intercomparison Project (PlioMIP): experimental design and boundary conditions (Experiment 2), Geosci. Model Dev., 4, 571–577, https://doi.org/10.5194/gmd-4-571-2011, 2011. a
Helsen, M. M., van de Berg, W. J., van de Wal, R. S. W., van den Broeke, M. R., and Oerlemans, J.: Coupled regional climate–ice-sheet simulation shows limited Greenland ice loss during the Eemian, Clim. Past, 9, 1773–1788, https://doi.org/10.5194/cp-9-1773-2013, 2013. a, b
Höning, D., Willeit, M., Calov, R., Klemann, V., Bagge, M., and Ganopolski, A.: Multistability and transient response of the Greenland ice sheet to anthropogenic CO2 emissions, Geophys. Res. Lett., 50, e2022GL101827, https://doi.org/10.1029/2022GL101827, 2023. a, b, c
Lawrence, D. M., Fisher, R. A., Koven, C. D., Oleson, K. W., Swenson, S. C., Bonan, G., Collier, N., Ghimire, B., van Kampenhout, L., Kennedy, D., Kluzek, E., Lawrence, P. J., Li, F., Li, H., Lombardozzi, D., Riley, W. J., Sacks, W. J., Shi, M., Vertenstein, M., Wieder, W. R., Xu, C., Ali, A. A., Badger, A. M., Bisht, G., van den Broeke, M., Brunke, M. A., Burns, S. P., Buzan, J., Clark, M., Craig, A., Dahlin, K., Drewniak, B., Fisher, J. B., Flanner, M., Fox, A. M., Gentine, P., Hoffman, F., Keppel-Aleks, G., Knox, R., Kumar, S., Lenaerts, J., Leung, L. R., Lipscomb, W. H., Lu, Y., Pandey, A., Pelletier, J. D., Perket, J., Randerson, J. T., Ricciuto, D. M., Sanderson, B. M., Slater, A., Subin, Z. M., Tang, J., Thomas, R. Q., Val Martin, M., and Zeng, X.: The Community Land Model version 5: Description of new features, benchmarking, and impact of forcing uncertainty, J. Adv. Model. Earth Sy., 11, 4245–4287, 2019. a, b
Le Meur, E. and Huybrechts, P.: A comparison of different ways of dealing with isostasy: examples from modelling the Antarctic ice sheet during the last glacial cycle, Ann. Glaciol., 23, 309–317, 1996. a
Lenton, T. M.: Early warning of climate tipping points, Nat. Clim. Change, 1, 201–209, 2011. a
Levermann, A., Clark, P. U., Marzeion, B., Milne, G. A., Pollard, D., Radic, V., and Robinson, A.: The multimillennial sea-level commitment of global warming, P. Natl. Acad. Sci. USA, 110, 13745–13750, 2013. a, b, c, d, e
Lipscomb, W. H., Price, S. F., Hoffman, M. J., Leguy, G. R., Bennett, A. R., Bradley, S. L., Evans, K. J., Fyke, J. G., Kennedy, J. H., Perego, M., Ranken, D. M., Sacks, W. J., Salinger, A. G., Vargo, L. J., and Worley, P. H.: Description and evaluation of the Community Ice Sheet Model (CISM) v2.1, Geosci. Model Dev., 12, 387–424, https://doi.org/10.5194/gmd-12-387-2019, 2019. a, b, c
Lofverstrom, M., Fyke, J. G., Thayer-Calder, K., Muntjewerf, L., Vizcaino, M., Sacks, W. J., Lipscomb, W. H., Otto-Bliesner, B. L., and Bradley, S. L.: An efficient ice sheet/Earth system model spin-up procedure for CESM2-CISM2: Description, evaluation, and broader applicability, J. Adv. Model. Earth Sy., 12, e2019MS001984, https://doi.org/10.1029/2019MS001984, 2020. a, b, c, d, e, f, g
Milne, G. A., Latychev, K., Schaeffer, A., Crowley, J. W., Lecavalier, B. S., and Audette, A.: The influence of lateral Earth structure on glacial isostatic adjustment in Greenland, Geophys. J. Int., 214, 1252–1266, 2018. a
Morlighem, M., Williams, C. N., Rignot, E., An, L., Arndt, J. E., Bamber, J. L., Catania, G., Chauché, N., Dowdeswell, J. A., Dorschel, B., Fenty, I., Hogan, K., Howat, I., Hubbard, A., Jakobsson, M., Jordan, T. M., Kjeldsen, K. K., Millan, R., Mayer, L., Mouginot, J., Noël, B. P. Y., O'Cofaigh, C., Palmer, S., Rysgaard, S., Seroussi, H., Siegert, M. J., Slabon, P., Straneo, F., van den Broeke, M. R., Weinrebe, W., Wood, M., and Zinglersen, K. B.: BedMachine v3: Complete bed topography and ocean bathymetry mapping of Greenland from multibeam echo sounding combined with mass conservation, Geophys. Res. Lett., 44, 11–051, 2017. a
Mouginot, J., Rignot, E., Bjørk, A. A., Van den Broeke, M., Millan, R., Morlighem, M., Noël, B., Scheuchl, B., and Wood, M.: Forty-six years of Greenland Ice Sheet mass balance from 1972 to 2018, P. Natl. Acad. Sci. USA, 116, 9239–9244, 2019. a, b, c, d
Muntjewerf, L., Petrini, M., Vizcaino, M., da Silva, C. E., Sellevold, R., Scherrenberg, M. D. W., Thayer-Calder, K., Bradley, S. L., Lenaerts, J. T. M., Lipscomb, W. H., and Lofverstrom, M.: Greenland Ice Sheet contribution to 21st century sea level rise as simulated by the coupled CESM2. 1-CISM2.1, Geophys. Res. Lett., 47, e2019GL086836, https://doi.org/10.1029/2019GL086836, 2020a. a, b, c
Muntjewerf, L., Sellevold, R., Vizcaino, M., Ernani da Silva, C., Petrini, M., Thayer-Calder, K., Scherrenberg, M. D. W., Bradley, S. L., Katsman, C. A., Fyke, J., Lipscomb, W. H., Lofverstrom, M., and Sacks, W. J.: Accelerated Greenland ice sheet mass loss under high greenhouse gas forcing as simulated by the coupled CESM2.1-CISM2. 1, J. Adv. Model. Earth Sy., 12, e2019MS002031, https://doi.org/10.1029/2019MS002031, 2020b. a, b, c, d, e, f
Muntjewerf, L., Sacks, W. J., Lofverstrom, M., Fyke, J., Lipscomb, W. H., Ernani da Silva, C., Vizcaino, M., Thayer-Calder, K., Lenaerts, J. T., and Sellevold, R.: Description and Demonstration of the Coupled Community Earth System Model v2–Community Ice Sheet Model v2 (CESM2-CISM2), J. Adv. Model. Earth Sy., 13, e2020MS002356, https://doi.org/10.1029/2020MS002356, 2021. a, b, c
NSF NCAR: Community Earth System Model 2 (CESM2), https://www.cesm.ucar.edu/models/cesm2, last access: 20 December 2024. a
Noël, B., van Kampenhout, L., van de Berg, W. J., Lenaerts, J. T. M., Wouters, B., and van den Broeke, M. R.: Brief communication: CESM2 climate forcing (1950–2014) yields realistic Greenland ice sheet surface mass balance, The Cryosphere, 14, 1425–1435, https://doi.org/10.5194/tc-14-1425-2020, 2020. a
Noël, B., van Kampenhout, L., Lenaerts, J., van de Berg, W., and Van Den Broeke, M.: A 21st century warming threshold for sustained Greenland ice sheet mass loss, Geophys. Res. Lett., 48, e2020GL090471, https://doi.org/10.1029/2020GL090471, 2021. a
Noël, B., Lenaerts, J. T., Lipscomb, W. H., Thayer-Calder, K., and van den Broeke, M. R.: Peak refreezing in the Greenland firn layer under future warming scenarios, Nat. Commun., 13, 6870, https://doi.org/10.1038/s41467-022-34524-x, 2022. a
Payne, A. J., Nowicki, S., Abe-Ouchi, A., Agosta, C., Alexander, P., Albrecht, T., Asay-Davis, X., Aschwanden, A., Barthel, A., Bracegirdle, T. J., Calov, R., Chambers, C., Choi, Y., Cullather, R., Cuzzone, J., Dumas, C., Edwards, T. L., Felikson, D., Fettweis, X., Galton-Fenzi, B. K., Goelzer, H., Gladstone, R., Golledge, N. R., Gregory, J. M., Greve, R., Hattermann, T., Hoffman, M. J., Humbert, A., Huybrechts, P., Jourdain, N. C., Kleiner, T., Munneke, P. K., Larour, E., Le clec'h, S., Lee, V., Leguy, G., Lipscomb, W. H., Little, C. M., Lowry, D. P., Morlighem, M., Nias, I., Pattyn, F., Pelle, T., Price, S. F., Quiquet, A., Reese, R., Rückamp, M., Schlegel, N.-J., Seroussi, H., Shepherd, A., Simon, E., Slater, D., Smith, R. S., Straneo, F., Sun, S., Tarasov, L., Trusel, L. D., Van Breedam, J., van de Wal, R., van den Broeke, M., Winkelmann, R., Zhao, C., Zhang, T., and Zwinger, T.: Future sea level change under coupled model intercomparison project phase 5 and phase 6 scenarios from the Greenland and Antarctic ice sheets, Geophys. Res. Lett., 48, e2020GL091741, https://doi.org/10.1029/2020GL091741, 2021. a
Petrini, M.: Supplementary video of Petrini et al. 2023, submitted to TC. “Topographically-controlled tipping point for complete Greenland Ice Sheet melt”, Zenodo [video], https://doi.org/10.5281/zenodo.8384527, 2023. a
Plach, A., Nisancioglu, K. H., Langebroek, P. M., Born, A., and Le clec'h, S.: Eemian Greenland ice sheet simulated with a higher-order model shows strong sensitivity to surface mass balance forcing, The Cryosphere, 13, 2133–2148, https://doi.org/10.5194/tc-13-2133-2019, 2019. a, b, c, d
Robinson, A., Calov, R., and Ganopolski, A.: Multistability and critical thresholds of the Greenland ice sheet, Nat. Clim. Change, 2, 429–432, 2012. a, b, c, d, e, f, g, h, i, j
Robinson, A., Goldberg, D., and Lipscomb, W. H.: A comparison of the stability and performance of depth-integrated ice-dynamics solvers, The Cryosphere, 16, 689–709, https://doi.org/10.5194/tc-16-689-2022, 2022. a
Rutt, I. C., Hagdorn, M., Hulton, N., and Payne, A.: The Glimmer community ice sheet model, J. Geophys. Res.-Earth, 114, F02004, https://doi.org/10.1029/2008JF001015, 2009. a, b
Sellevold, R. and Vizcaíno, M.: Global warming threshold and mechanisms for accelerated Greenland ice sheet surface mass loss, J. Adv. Model. Earth Sy., 12, e2019MS002029, https://doi.org/10.1029/2019MS002029, 2020. a, b
Sellevold, R., van Kampenhout, L., Lenaerts, J. T. M., Noël, B., Lipscomb, W. H., and Vizcaino, M.: Surface mass balance downscaling through elevation classes in an Earth system model: application to the Greenland ice sheet, The Cryosphere, 13, 3193–3208, https://doi.org/10.5194/tc-13-3193-2019, 2019. a
Shepherd, A., Ivins, E. R., A, G., Barletta, V. R., Bentley, M. J., Bettadpur, S., Briggs, K. H., Bromwich, D. H., Forsberg, R., Galin, N., Horwath, M., Jacobs, S., Joughin, I., King, M. A., Lenaerts, J. T. M., Li, J., Ligtenberg, S. R. M., Luckman, A., Luthcke, S. B., McMillan, M., Meister, R., Milne, G., Mouginot, J., Muir, A., Nicolas, J. P., Paden, J., Payne, A. J., Pritchard, H., Rignot, E., Rott, H., Sørensen, L. S., Scambos, T. A., Scheuchl, B., Schrama, E. J. O., Smith, B., Sundal, A. V., van Angelen, J. H., van de Berg, W. J., van den Broeke, M. R., Vaughan, D. G., Velicogna, I., Wahr, J., Whitehouse, P. L., Wingham, D. J., Yi, D., Young, D., and Zwally, H. J.: A reconciled estimate of ice-sheet mass balance, Science, 338, 1183–1189, 2012. a
Sommers, A. N., Otto-Bliesner, B. L., Lipscomb, W. H., Lofverstrom, M., Shafer, S. L., Bartlein, P. J., Brady, E. C., Kluzek, E., Leguy, G., Thayer-Calder, K., and Tomas, R. A.: Retreat and Regrowth of the Greenland Ice Sheet During the Last Interglacial as Simulated by the CESM2-CISM2 Coupled Climate–Ice Sheet Model, Paleoceanography and Paleoclimatology, 36, e2021PA004272, https://doi.org/10.1029/2021PA004272, 2021. a, b, c, d
The IMBIE Team: Mass balance of the Greenland Ice Sheet from 1992 to 2018, Nature, 579, 233–239, 2020. a
Van Breedam, J., Goelzer, H., and Huybrechts, P.: Semi-equilibrated global sea-level change projections for the next 10 000 years, Earth Syst. Dynam., 11, 953–976, https://doi.org/10.5194/esd-11-953-2020, 2020. a
van Kampenhout, L., Lenaerts, J. T., Lipscomb, W. H., Lhermitte, S., Noël, B., Vizcaíno, M., Sacks, W. J., and van den Broeke, M. R.: Present-day Greenland ice sheet climate and surface mass balance in CESM2, J. Geophys. Res.-Earth, 125, e2019JF005318, https://doi.org/10.1029/2019JF005318, 2020. a
Vizcaino, M., Mikolajewicz, U., Ziemen, F., Rodehacke, C. B., Greve, R., and van den Broeke, M. R.: Coupled simulations of Greenland Ice Sheet and climate change up to AD 2300, Geophys. Res. Lett., 42, 3927–3935, 2015. a
Wake, L. M., Lecavalier, B. S., and Bevis, M.: Glacial isostatic adjustment (GIA) in Greenland: A review, Current Climate Change Reports, 2, 101–111, 2016. a
Walcott, R.: Flexural rigidity, thickness, and viscosity of the lithosphere, J. Geophys. Res., 75, 3941–3954, 1970. a
Zeitz, M., Reese, R., Beckmann, J., Krebs-Kanzow, U., and Winkelmann, R.: Impact of the melt–albedo feedback on the future evolution of the Greenland Ice Sheet with PISM-dEBM-simple, The Cryosphere, 15, 5739–5764, https://doi.org/10.5194/tc-15-5739-2021, 2021. a
Zeitz, M., Haacker, J. M., Donges, J. F., Albrecht, T., and Winkelmann, R.: Dynamic regimes of the Greenland Ice Sheet emerging from interacting melt–elevation and glacial isostatic adjustment feedbacks, Earth Syst. Dynam., 13, 1077–1096, https://doi.org/10.5194/esd-13-1077-2022, 2022. a, b, c, d, e, f, g
Zweck, C. and Huybrechts, P.: Modeling of the northern hemisphere ice sheets during the last glacial cycle and glaciological sensitivity, J. Geophys. Res.-Atmos., 110, D07103, https://doi.org/10.1029/2004JD005489, 2005. a