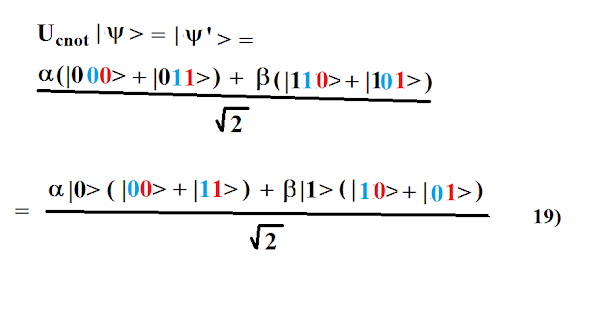ABSTRACT:
Quantum entanglement can be explained using decks of cards. This paper shows how these decks of cards violate Bell's inequality, and that "hidden operators" determine a quantum measurement outcome. If these hidden operators could be known prior to measurement, one could predict the outcomes of quantum events. The herein thought experiment demonstrates that no faster-than-light communication takes place between entangled pairs. Further, when teleportation is scrutinized, there is no evidence that information passes through a wormhole.
According to John Stewart Bell, the following thought experiment should not violate his famous inequality: Start with two decks of cards joined together along the red-dotted line:
Because they are joined together, when the decks are randomly shuffled, they correlate (or anti-correlate). Now, divide the two decks along the same red-dotted line. Send one to Alice and the other to Bob. On the face of each card is a |0> or |1>. Neither Alice nor Bob know what card they will each deal from the top of their respective decks. It is as if the decks are in a state of superposition. However, if Alice deals a |0>, she knows which card Bob has dealt. Note there is no communication going on between the decks. They can be any distance apart and Alice will instantaneously know which card Bob has dealt.
Now, if Alice could just take a peek at the cards hidden in her deck before she deals them, she would be able to predict which card she will deal next with 100% certainty.
So, does this thought experiment demonstrate, by analogy, quantum entanglement? There is a test. Let's have Alice and Bob send each of their dealt cards to three polarizers: A, B and C. There is a chance each card will pass through one or more of the polarizers, or none at all. Alice and Bob keep track of the results and each create a data table matching the one below:
Since their datasets are identical, let's focus on Alice's. If a card passed through polarizer A, Alice records a 1, otherwise she records a 0. Same goes for polarizers B and C. At the right of the table, Alice checks if a card passed through A but not B (A!B). If so, she records a 1; otherwise, she records a 0. Then she checks if a card passed through B but not C (B!C) and records the result, and finally, she checks if a card passed through A but not C (A!C). She then adds up the columns. The final result is 2 + 2 is greater than or equal to 2. This is consistent with Bell's inequality:

Thus, according to Bell, the above thought experiment fails to accurately describe quantum entanglement. But what if Bell is wrong? Let's explore this possibility. Equation 2 below is another way to express Bell's inequality. It is expressed in terms of probabilities, sines and cosines, and, most importantly, it is a function of the polarizers' angles. Equations 3, 4, and 5 show that the data at the data table's first row would not be possible if the polarization angles were anything but zero or ninety degrees. This implies that the cards were oriented either vertically or horizontally (90 degrees or 0 degrees) and the polarizer slits were also vertical or horizontal (90 degrees or 0 degrees).

What if the polarization angles were not just zero or ninety degrees? Would Bell's inequality still be valid or would it be violated? Let's modify the above thought experiment. Suppose the cards are made of elastic material that enables them to squeeze through any opening; although, this is not guaranteed--there is a probability a card will squeeze through a polarizer that has an arbitrary polarization angle. Let's see if the cards can violate Bell's inequality if the polarization angles are altered.
Let's assume Alice's deck and Bob's deck are anti-correlated. If Alice deals a |0>, Bob deals a |1>. Below are the probabilities that their cards will pass through polarizers A, B and C:
On the left side of each equation above, the first term is the probablity that a card will pass through a given polarizer; the second term is the probability that a card will fail to pass through. Note that the probabilities add up to one as they should. Also note that the polarization angles are represented by theta-A, theta-B and theta-C. Using the above information, we can create the following version of Bell's inequality:
The first term is the probability of Alice's card passing through A times the probability of Bob's card not passing through B. The second term is the probability of Alice's card passing through B times the probability of Bob's card not passing through C. Finally, the term on the right of the inequality is the probability of Alice's card passing through A times the probability of Bob's card not passing through C. Using equation 6 above, we can calculate what polarization angles are needed to violate Bell's inequality:
At 9 above, we see that if theta-B is less than the term to its right, Bell's inequality will in fact be violated. Of course, theta-B is an arbitrary label. Let's swap it with theta-A:
At 11 above, we assign new angles to polarizers A, B and C: 0 degrees, 22.5 degrees and 45 degrees, respectively. When we plug these angles into inequality 6 and inequality 10, we find that our two decks of cards do in fact violate Bell's inequality. This means that the above thought experiment is an accurate analogy of the workings of quantum entanglement. It also implies that Einstein, Podolsky and Rosen (EPR) had an idea that may be valid after all: "hidden variables." This idea is not so far-fetched when you consider the fact that quantum mechanics has hidden operators. Here are a couple of examples:

The hidden operators are labeled in red. They are the NOT (X) and Identity (I) operators. When given a state of superposition, they secretly conspire with the Hadamard operator (H) to determine the outcome of a measurement. The result seems random to us, since we can't examine these hidden operators ahead of any measurement. Even if we could, we would know the order of the cards in the deck, so to speak, but we still wouldn't know how they got that way. We would be forced to fall back on, "They were randomly shuffled." Nevertheless, Alice could predict what her next card is going to be. She could even know ahead of time if the card will make it through a polarizer, since she might also know the "hidden probability operators."
Even if Alice can never know any hidden operators, she knows which card Bob dealt even if he is light-years away, and, the cards violate Bell's inequality. It appears the two decks of cards are truly entangled--is there a wormhole connecting them? If not, how does quantum teleportation work?
There is a five-step teleportation process that apparently shows that Alice can instantaneously send a qubit to Bob, allegedly through a wormhole. Let's examine this process.
Alice wants to send Bob the following qubit (greek letter chi):
Teleportation step 1: Alice and Bob share an entangled pair of particles:
Find the tensor product of chi and the entangled pair:
Note that chi, Alice, and Bob's zeros and ones are colored black, blue and red, respectively. This enables us to track them. Now, we can use the table below to represent the original state of the system. The table has n units of ones and zeros in each column. The top portion has (alpha^2)n units, the bottom portion has (Beta^2)n units.
Teleportation step 2: Alice applies a CNOT gate:
Let's update the table:
Notice that Alice and Bob are no longer entangled! There is no guarantee that their ones and zeros will match. Technically this implies the wormhole is now closed or non-existent, since wormholes allegedly depend on entanglement. Yet, somehow Alice still manages to send the qubit to Bob? Let's continue. Step 3: Alice applies a Hadamard gate:
Time to update the table:
Step 4: Alice measures her pair (which includes chi's one or zero, and her own). Looking at the table above, notice that no changes were ever made to Bob's ones and zeros. Bob's final state is identical to his original state; yet, for example, when chi and Alice have a |00>, there is an alpha^2 probability Bob will have a |0> and a beta^2 probability Bob will have a |1>. Equation 22 confirms this. It's as if Alice really teleported the chi qubit to Bob, but Bob has no clue Alice tried to teleport anything. That's why step 5 is necessary. Alice must send Bob a no-faster-than-light signal through normal channels to let him know about her new disentangled measurements and what gates he must apply. But wouldn't it be faster if Alice uses the wormhole for step 5? What wormhole?
It should be reasonably obvious at this point that entanglement exists without the aid of wormholes or faster-than-light communication. Teleportation seems to work if both Bob and Alice assume Alice's ones and zeros have not changed; therefore, when they compare notes, it seems like Bob's ones and zeros take on new probabilities. This reminds me of relativity, where the train passes the station, or, is it the station that passes the train?
Acknowledgements:
Special thanks to ChatGPT4.
References:
1. Einstein, A., Poldolsky, B., Rosen, N. 03/25/1935. Can Quantum-Mechanical Description of Reality Be Considered Complete. Physical Review, Volume 47.
2. Leonard Susskind | "ER = EPR" or "What's Behind the Horizons of Black Holes?"". Archived from the original on 2021-12-11 – via www.youtube.com.
3. Einstein, A. Rosen, N. 07/01/1935. The Particle Problem in the Theory of General Relativity. Physical Review. 48.
4. McMahon, David. 2008. Quantum Computing Explained. John Wiley and Sons Inc.
5. Fadelli, Ingrid. 09/21/2023. A model probing the connection between entangled particles and wormholes in general relativity. Phys.org
6. Bell's Theorem. Wikipedia, ChatGPT4, and various online sources.