O que mais cai em Matemática no Enem?

O Exame Nacional do Ensino Médio (Enem) é uma das principais portas de entrada para o ensino superior no Brasil, sendo a prova mais aguardada por milhões de estudantes. Entre as áreas do conhecimento, a prova de Matemática se destaca como um dos maiores desafios, composta por 45 questões que abrangem diversos tópicos. 

Pensando nisso, separamos para você os temas que mais caem na prova de Matemática do Enem. Assim, você pode aprender tudo que precisa antes do dia do exame, sendo um grande diferencial para você garantir uma boa pontuação e conquistar uma vaga na universidade desejada. 

Acompanhe abaixo!  👇 

O que mais cai na prova de Matemática do Enem?

A prova de Matemática do Enem é conhecida por sua complexidade. No entanto, alguns assuntos aparecem com mais frequência e merecem uma atenção especial durante a preparação. 

Entre os principais estão Matemática Básica, Estatística, Geometria Espacial, Geometria Plana e Funções. Cada um desses tópicos abrange conceitos fundamentais para qualquer estudante que irá fazer o Enem. 

Veja o que mais cai em matemática no Enem: 

1. Matemática básica

A Matemática básica é o alicerce de muitas questões no Enem, sendo um dos tópicos mais recorrentes nas provas. Ela abrange vários conceitos fundamentais que servem como base para resolver problemas mais complexos. 

Dentre os conteúdos mais importantes para revisar estão: 

• números inteiros;
• frações;
• números decimais;
• potenciação;
• radiciação;
• transformação de unidades;
• equações do primeiro e segundo grau;
• porcentagem;
• razão e proporção;
• regra de três.

Abaixo, detalhamos alguns desses principais tópicos para você aprender. 

Regra de três

A regra de três é uma ferramenta essencial em Matemática básica, usada para encontrar valores desconhecidos quando se trabalha com grandezas proporcionais. Essa técnica é útil em problemas que envolvem razão e proporção.

Para aplicar a regra de três, o estudante deve entender o conceito de grandezas proporcionais. 

Em termos simples, uma razão é a relação entre dois valores de uma mesma grandeza, enquanto a proporção indica uma igualdade entre duas razões. Grandezas proporcionais são aquelas em que a variação de uma causa uma variação correspondente na outra.

Grandezas podem ser diretamente ou inversamente proporcionais:

• Grandezas diretamente proporcionais: se uma grandeza aumenta, a outra aumenta na mesma proporção. Da mesma forma, se uma diminui, a outra também diminui proporcionalmente;
• Grandezas inversamente proporcionais: se uma grandeza aumenta, a outra diminui na mesma proporção, e vice-versa.

Regra de três simples

A regra de três simples é usada quando o problema envolve apenas duas grandezas que são diretamente ou inversamente proporcionais. Aqui, você tem uma relação simples: se você conhece três valores, pode encontrar o quarto desconhecido. 

Exemplo: 

Suponha que 5 maçãs custem R$10. Quanto custariam 8 maçãs? 

Como estamos lidando com grandezas diretamente proporcionais (mais maçãs, mais custo), montamos a proporção e resolvemos facilmente para encontrar o valor desconhecido.

Montando a proporção:

5 ÷ 10 = 8 ÷ x

Onde:

5 é a quantidade de maçãs;

10 é o custo em reais;

8 é a nova quantidade de maçãs;

x é o custo desconhecido.

Resolvendo a proporção:

5 × X=10 × 8

5x=80

x= 16

Regra de três composta

A regra de três composta entra em cena quando o problema envolve mais de duas grandezas. Nesse caso, você precisará analisar a relação entre cada par de grandezas (se são diretamente ou inversamente proporcionais) e montar uma sequência de proporções. 

Esse tipo de regra de três é mais complexo e exige uma atenção maior na hora de identificar corretamente todas as grandezas envolvidas.

Exemplo: 

Se 3 pedreiros constroem uma parede em 10 dias, quantos pedreiros seriam necessários para construir a mesma parede em 6 dias, trabalhando o dobro de horas por dia? 

Aqui, temos três grandezas: número de pedreiros, tempo em dias, e horas de trabalho por dia, exigindo uma abordagem composta para resolver o problema.

Número de pedreiros 1  ÷  Número de pedreiros 2 = Dias 2  ÷   Dias 1 x Horas 1 ÷  Horas 2

Substituindo os valores conhecidos:

3 ÷  x = 6  ÷ 10 x 1 ÷ 2

Agora, resolvemos a proporção:

3 ÷ x = 3 ÷ 10

Multiplicando em cruz:

3×10=3 × x

30 = 3x

x = 10 

2. Funções

Funções são um dos temas centrais na prova de Matemática do Enem, e o domínio desse assunto é essencial para garantir um bom desempenho. 

Entre os temas sobre funções que mais caem em matemática no Enem, o foco principal está nas funções do primeiro e segundo grau, além da análise de crescimento e decrescimento, inequações e análise de máximos e mínimos.

Função do primeiro grau

A função do primeiro grau é uma das mais versáteis e frequentemente aparece tanto em Matemática quanto em Física no Enem. Sua forma algébrica é:

f(x) = ax + b

Aqui, os coeficientes a e b são fundamentais para a interpretação da função:

• Coeficiente a: conhecido como coeficiente angular, ele indica se a reta é crescente (a>0) ou decrescente (a<0).
• Coeficiente b: chamado de coeficiente linear, este valor indica o ponto em que a reta intercepta o eixo y.
• Raiz ou zero da função: é o valor de x que faz f(x)=0, ou seja, o ponto onde a reta cruza o eixo x.

Função do segundo grau

A função do segundo grau, ou função quadrática, é outra protagonista do Enem. Sua forma algébrica é:

f(x) = ax² + bx + c

Nesta função, o comportamento é definido pelos coeficientes a, b e c:

• Coeficiente a: determina a concavidade da parábola; a>0 indica concavidade para cima e a<0 indica concavidade para baixo.
• Coeficiente c: indica onde a parábola intercepta o eixo y.
• Raízes ou zeros da função: são os pontos onde a parábola toca o eixo x, calculados pela fórmula de Bhaskara ou pelo método de soma e produto.
• Vértice da parábola: representa o ponto de máximo ou mínimo da função e é encontrado pelas fórmulas: 

A compreensão desses elementos ajuda o estudante a resolver as questões que mais caem de matemática no Enem envolvendo a análise gráfica e numérica de funções quadráticas.

Nomenclaturas e padrões gráficos

É comum que as questões do Enem utilizem termos específicos ou gráficos que não explicitam claramente o tipo de função envolvida. Por isso, conhecer as nomenclaturas e os padrões gráficos é uma vantagem na hora de realizar a prova:

• Funções de Primeiro Grau: termos como “linear”, “proporcional” e “função afim” indicam funções do tipo f(x)=ax+b.
• Funções de Segundo Grau: termos como “parábola” e “funções quadráticas” referem-se a funções do tipo 𝑓(𝑥)=𝑎𝑥²+𝑏𝑥+𝑐
• Funções Trigonométricas: gráficos com padrões periódicos e repetitivos.
• Funções Constantes: gráficos de retas horizontais, indicando que a função é constante.

3. Geometria espacial

Na geometria espacial há dois subtemas que se destacam: a geometria de posição e os cálculos de volumes e áreas de sólidos como prismas e cilindros. Entenda cada um deles!

Geometria de posição

A geometria de posição lida com as relações de posição entre retas e planos. Nesse contexto, os problemas exigem a compreensão de conceitos como:

• Reta perpendicular a um plano: quando uma reta forma um ângulo de 90 graus com um plano, dizemos que ela é perpendicular a esse plano.
• Reta oblíqua a um plano: quando a reta não é perpendicular, ela é chamada de oblíqua, e a projeção dessa reta no plano é uma linha inclinada que mostra a inclinação em relação ao plano.

Esses conceitos costumam cair na prova do Enem e são representados graficamente Portanto, exigem uma análise cuidadosa das posições relativas entre as retas e os planos.

Volumes e áreas

O cálculo de volumes e áreas de sólidos, especialmente prismas e cilindros, também é um assunto recorrente no Enem. A fórmula para calcular o volume desses sólidos é:

V=AB×h

Onde:

• AB: Área da base do sólido.
• h: Altura do sólido.

Para calcular a área total de prismas e cilindros, é necessário somar a área das duas bases com a área lateral:

AT = 2 x AB + AL

Onde:

• AL: Área lateral do sólido.

Esses cálculos são cruciais, especialmente em questões do Enem onde o volume está associado à capacidade interna de um sólido, medida em metros cúbicos (m³) ou litros.

4. Estatística

A estatística no Enem entra nas questões para interpretar dados e aplicar medidas de tendência central. Veja:

Interpretação de gráficos e tabelas

Gráficos e tabelas são utilizados para representar dados de forma visual e objetiva. Confira alguns tipos de gráficos comuns e suas aplicações:

• Gráficos de barras: utilizados para mostrar a frequência de diferentes categorias. Cada barra representa uma categoria e a altura da barra reflete a quantidade ou frequência dessa categoria.
• Gráficos de linhas: ideal para representar dados ao longo do tempo, mostrando tendências e variações em períodos consecutivos.
• Gráficos de setores (Pizza): mostram a distribuição proporcional dos dados em diferentes categorias, com cada setor representando uma parte do todo.

Além dos gráficos, as tabelas organizam informações em linhas e colunas, permitindo uma visualização clara das quantidades e categorias. Em questões desse tipo, a leitura atenta do enunciado é essencial para identificar quais partes dos gráficos ou tabelas são relevantes para responder às perguntas.

Medidas de tendência central (MTC)

As medidas de tendência central servem para descrever e resumir conjuntos de dados. No Enem, as principais medidas cobradas são:

Moda: a moda é o valor que aparece com maior frequência em um conjunto de dados. Se mais de um valor se repete com a mesma frequência máxima, o conjunto pode ter mais de uma moda;

Média: a média é a soma de todos os valores dividida pelo número total de valores. 

Existem diferentes tipos de médias, mas as mais comuns são:

• Média aritmética simples: calculada somando todos os valores e dividindo pelo número total de valores.
• Média aritmética ponderada: calculada multiplicando cada valor por um peso específico, somando os resultados e dividindo pela soma dos pesos.

Mediana: a mediana é o valor central quando os dados são organizados em ordem crescente. Se houver um número par de dados, a mediana é a média dos dois valores centrais.

Entender e aplicar essas medidas permite que você descreva e interprete conjuntos de dados de forma eficaz, facilitando a resolução das questões de estatística no Enem.

5. Geometria plana

A geometria plana cobre tópicos como polígonos regulares, circunferência e círculo, e fórmulas de áreas. Veja abaixo o que pode cair deste tema em matemática no Enem: 

Polígonos regulares

Polígonos regulares são figuras planas com todos os lados e ângulos iguais. No Enem, os polígonos regulares mais comuns são:

Triângulo Equilátero: todos os três lados e ângulos são iguais. A fórmula para a área é:

onde s é o comprimento de um lado.

Quadrado: todos os quatro lados e ângulos são iguais. A fórmula para a área é:

A=s²

onde s é o comprimento de um lado.

Hexágono Regular: possui seis lados iguais e ângulos iguais. A fórmula para a área é:

onde s é o comprimento de um lado.

Circunferência e círculo

Para a circunferência e o círculo, é importante saber calcular suas propriedades básicas:

Círculo: a área 𝐴 do círculo é dada por:

A=πr ²

onde 𝑟 é o raio do círculo.

Circunferência: o comprimento 𝐶 da circunferência é dado por:

C=2πr

onde r é o raio do círculo.

Além disso, é útil saber calcular áreas de setores e segmentos circulares, embora esses tópicos sejam menos frequentes no Enem.

Fórmulas de áreas recorrentes

A área de figuras planas é também um ponto frequente nas questões do Enem. Veja as principais fórmulas: 

Triângulo: a fórmula para a área é:

onde 𝑏 é a base e ℎ é a altura.

Retângulo: A fórmula para a área é:

A=b×h

onde 𝑏 é a base e ℎ é a altura.

Trapézio: A fórmula para a área é:

onde 𝑏1  e 𝑏2 ​ são as bases e ℎ é a altura.

Para figuras mais complexas, como polígonos com muitos lados, você pode precisar dividir a figura em formas mais simples e somar as áreas dessas formas. 

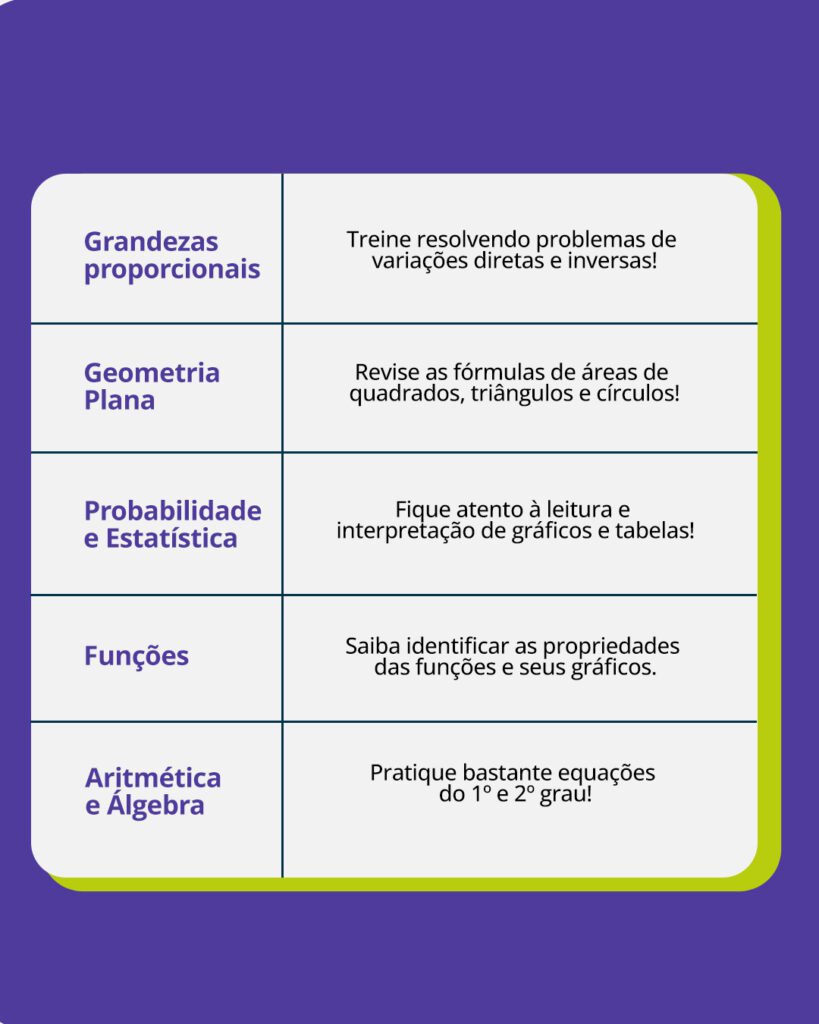
Como ir bem na prova de Matemática do Enem?

Para conquistar uma boa nota em Matemática no Enem é preciso adotar uma estratégia de estudo com muito foco e dedicação. Reunimos as principais dicas para você ir bem nos assuntos que mais caem de Matemática no Enem:

Domine os conceitos fundamentais

Entender os conceitos por trás das fórmulas é mais eficiente do que apenas memorizá-las. Dedique seu tempo em aprender a lógica por trás dos tópicos e como aplicá-los a diferentes tipos de problemas. Para isso, resumos teóricos podem ajudar a reter esse conhecimento e facilitar a revisão.

Pratique questões de matemática regularmente

A prática é fundamental para a preparação no Enem. Por isso, resolva questões de provas anteriores do Enem para se familiarizar com o estilo das perguntas e com os temas mais recorrentes. 

Na Estuda.com, você conta com um banco de questões completa para treinar. Abra sua conta gratuita e aproveite! 

Isso não só ajuda a identificar áreas que precisam de mais atenção, mas também a melhorar suas habilidades de resolução de problemas.

Desenvolva habilidades de interpretação

A interpretação dos enunciados é fundamental para ir bem no Enem. Durante o exame, leia atentamente os enunciados e destaque as informações importantes. Muitas vezes, compreender o que está sendo pedido é mais valioso do que conhecer a fórmula exata.

Utilize diversas técnicas de estudo

Incorporar métodos variados pode tornar o estudo mais eficaz e interessante. Use técnicas como mapas mentais, videoaulas, e resumos. Essas estratégias ajudam a consolidar o conhecimento e a manter o estudo envolvente.

Treine sem calculadora

No Enem, você não poderá contar com sua calculadora que está no celular sempre com você! Por isso, pratique resolver questões sem o uso dessa ferramenta para aprimorar suas habilidades de cálculo mental e rápida escrita. 

Seguindo essas dicas práticas e absorvendo todos os temas que mais caem em Matemática no Enem, você estará bem preparado para enfrentar a prova. Boa sorte na sua preparação!

Se precisar de ajuda, conte com a Estuda! 😉☘️💙💚