Published online by Cambridge University Press: 12 March 2014
A first-order sentence is quasi-modal if its class of models is closed under the modal validity preserving constructions of disjoint unions, inner substructures and bounded epimorphic images.
It is shown that all members of the proper class of canonical structures of a modal logic Λ have the same quasi-modal first-order theory ΨΛ. The models of this theory determine a modal logic Λe which is the largest sublogic of Λ to be determined by an elementary class. The canonical structures of Λe also have ΨΛ as their quasi-modal theory.
In addition there is a largest sublogic Λe of Λ that is determined by its canonical structures, and again the canonical structures of Λe have ΨΛ are their quasi-modal theory. Thus 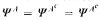 . Finally, we show that all finite structures validating Λ are models of ΨΛ, and that if Λ is determined by its finite structures, then ΨΛ is equal to the quasi-modal theory of these structures.
. Finally, we show that all finite structures validating Λ are models of ΨΛ, and that if Λ is determined by its finite structures, then ΨΛ is equal to the quasi-modal theory of these structures.