Abstract
Uncertainty in model projections of future climate change arises due to internal variability, multiple possible emission scenarios, and different model responses to anthropogenic forcing. To robustly quantify uncertainty in multi-model ensembles, inter-dependencies between models as well as a models ability to reproduce observations should be considered. Here, a model weighting approach, which accounts for both independence and performance, is applied to European temperature and precipitation projections from the CMIP5 archive. Two future periods representing mid- and end-of-century conditions driven by the high-emission scenario RCP8.5 are investigated. To inform the weighting, six diagnostics based on three observational estimates are used to also account for uncertainty in the observational record. Our findings show that weighting the ensemble can reduce the interquartile spread by more than 20% in some regions, increasing the reliability of projected changes. The mean temperature change is most notably impacted by the weighting in the Mediterranean, where it is found to be 0.35 °C higher than the unweighted mean in the end-of-century period. For precipitation the largest differences are found for Northern Europe, with a relative decrease in precipitation of 2.4% and 3.4% for the two future periods compared to the unweighted case. Based on a perfect model test, it is found that weighting the ensemble leads to an increase in the investigated skill score for temperature and precipitation while minimizing the probability of overfitting.

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Changes in the climate system due to anthropogenic greenhouse gas emissions affect society through rising temperatures and changing precipitation patterns, among other things (IPCC 2013, WMO 2019). Efforts are ongoing to limit global mean warming to well below 2 °C in order to avoid dangerous levels of climate change (United Nations 2015). On a regional scale, however, temperature and precipitation changes can vastly differ from the global average (Seneviratne et al 2018) and uncertainties are often larger (Hawkins and Sutton 2009, Deser et al 2012a) . On such scales it is, therefore, even more important for decision makers, such as politicians and large infrastructure providers, to make decisions based on the best available knowledge.
Efforts are ongoing in the scientific community to deliver such reliable and actionable information on relevant temporal and spatial scales, for example, within the European Climate Prediction system (EUCP) project (Hewitt and Lowe 2018). The EUCP aims to combine regional and global climate model projections from the latest Coupled Model Intercomparison Projects CMIP5 (Taylor et al 2012) and CMIP6 (Eyring et al 2016) with targeted statistical approaches to reduce uncertainty in multi-model mean projections of regional climate.
Model projections are affected by a range of uncertainties including emissions scenario uncertainty, internal variability of the climate system, and model response uncertainty (Hawkins and Sutton 2009). Scenario uncertainty takes into account different possible socio-economic developments (van Vuuren et al 2011, O'Neill et al 2014) and is as such mainly determined by political decisions and technological development. Internal variability arises from the chaotic behavior of the weather and can not be reduced when investigating a given region and time period of interest (Hawkins and Sutton 2009, Deser et al 2012b, Fatichi et al 2016).
Hence, reducing the model spread is often the only option to reduce total uncertainty of climate model projections. Many different approaches have been used in the past, based on the assumption that the reliability of a model in the future can be inferred from its performance in reproducing historical climate. These approaches argue that some models may be more 'fit for purpose' for a given application (e.g. variable, region, or lead time) than others (Gleckler et al 2008, Parker 2009, Knutti 2010, Baumberger et al 2017, Eyring et al 2019), and thus deserve to receive more weight in the multi-model estimate of change.
In addition, when working with an 'ensemble of opportunity' (Tebaldi and Knutti 2007) such as CMIP5, the handling of model inter-dependencies becomes an important question to address. The models contributing to CMIP5 were not designed to be independent from each other: developers might have shared ideas and code, some models might use identical components, or two models might have been branched from the same parent (Knutti et al 2013, Sanderson et al 2015a, Annan and Hargreaves 2017, Abramowitz et al 2019, Eyring et al 2019). Moreover, for several models, multiple realizations with slightly perturbed initial conditions are provided. On the one hand, such ensembles should not simply be included in a multi-model estimate, since they represent the same model, hence artificially increasing the weight of models with more members. On the other hand, using only one member per model discards the additional information provided by these initial condition ensembles.
The raw model range of the full CMIP5 ensemble, hence, does not necessarily represent the actual uncertainty of the climate system. It rather reflects the ensemble design (or a lack thereof) and can either overestimate or underestimate the actual uncertainty (Lorenz et al 2018). To better capture real uncertainty different methods account for model performance and independence by selecting only a subset of models (Pennell and Reichler 2011, Evans et al 2013, Leduc et al 2016, Hegerl et al 2018, Herger et al 2019), finding emergent constraints for the change in an investigated variable (Hall and Qu 2006, Gordon and Klein 2014, Cox et al 2018, Hall et al 2019), or model weighting (Coppola et al 2010, Abramowitz and Bishop 2015, Knutti et al 2017, Sanderson et al 2017, Lorenz et al 2018).
We here use a model weighting approach which accounts for model performance and independence (Sanderson et al 2015a, 2015b, Knutti et al 2017, Lorenz et al 2018). In an initial step our study focuses on selecting relevant diagnostics to establish model performance and independence. For the first time we use multiple observational data sets to inform this method and to include an estimate of observational uncertainty. Calculated weights are then applied to projections of temperature and precipitation change in eight different regions in Europe and in two future periods. The selection of these regions and time periods is party guided by a coordinated effort by the EUCP to compare different methods constraining European climate projections to which this work is contributing. In addition, the selected regions allow for a discussion of the weighting performance in different parts of Europe and for three distinctively different regions sizes. Ultimately the aim of this study is to better quantify the uncertainty of future changes and to improve projection skill as well as enable the usage of full multi-model ensembles without having to manually account for multiple initial condition members or model dependencies.
2. Data and methods
2.1. Model data
This study is based on all available CMIP5 models which contain the variables required to inform the weighting (37 models with a total of 79 realizations; see figure S6 in the supplement for a full list). We use monthly data, regridded to a regular 2.5° × 2.5° grid using bi-linear remapping. Throughout the study, we base our weighting approach on the base-period 1995–2014 in the combined historical and Representative Concentration Pathway 8.5 (RCP8.5) (van Vuuren et al 2011) forcing runs, and apply the weights to RCP8.5 forcing runs for the future projections. The base-period is selected to (i) best represent present day conditions and (ii) in anticipation of and to be easily comparable to the upcoming CMIP6 which uses historical forcing up to 2014 (Eyring et al 2016).
2.2. Observation-based datasets
To account for uncertainties in the observational records, the performance weighting is based on observational estimates from two reanalysis datasets and one combined observational dataset. We use the interim reanalysis from the European Centre for Medium-Range Weather Forecasts (ERA-Interim) (Dee et al 2011) and the Modern-Era Retrospective analysis for Research and Applications version 2 from the National Aeronautics and Space Administration (MERRA2) (Gelaro et al 2017). In addition, we use a combined observational dataset, which is based on the ensemble version 17 of E-OBS (Cornes et al 2018) (for temperature, precipitation, sea level pressure) and the CERES EBAF Surface Ed2.8 (Kato et al 2013) (for radiation variables).
2.3. Model weighting
We focus on changes in summer (JJA) temperature and precipitation in the three European SREX (IPCC 2012) regions: Northern Europe (NEU), Central Europe (CEU), and the Mediterranean (MED) as well as in the combined European domain (EUR). In addition, we test the performance of the method on four single grid cells as listed in table 1. A geographical map showing all regions as well as the model resolution and the applied land-sea mask can be found in the supplement (figure S1 is available online at stacks.iop.org/ERL/14/124010/mmedia). The effects of the weighting on future projections for two 20-year periods representing mid-century (2041–2060) and end-of-century (2081–2100) conditions are investigated.
Table 1. Regions and shape parameters (σD and σS) used in this study. The coordinates for the last four regions give the center of the 2.5° × 2.5° grid cell used.
| Key | Name | Location | σD (tas) | σD (pr) | σS |
|---|---|---|---|---|---|
| EUR | Europe | NEU + CEU + MED | 0.588 | 0.658 | 0.704 |
| NEU | Northern Europe | NEU | 0.614 | 0.542 | 0.735 |
| CEU | Central Europe | CEU | 0.607 | 0.831 | 0.706 |
| MED | Mediterranean | MED | 0.546 | 0.667 | 0.643 |
| FAL | Falun (Sweden) | 13.75 °E, 61.25 °N (NEU) | 0.852 | 0.800 | 0.628 |
| DUS | Dusseldorf (Germany) | 6.25 °E, 51.25 °N (CEU) | 0.929 | 0.956 | 0.790 |
| SIB | Sibiu (Romania) | 23.75 °E, 46.25 °N (CEU) | 1.030 | 1.227 | 0.691 |
| MAD | Madrid (Spain) | −3.75 °E, 41.25 °N (MED) | 1.116 | 1.089 | 0.604 |
Weights are calculated for each model following the approach presented by Lorenz et al (2018), which is based on earlier work from Knutti et al (2017) and Sanderson et al (2015a, 2015b). Each weight wi is a combination of the observational distance Di (informing the performance weighting) and the model distance Sij (informing the independence weighting):

with the total number of model runs M and the shape parameters σD and σS. The shape parameters define the strength of the weighting and the relative importance of performance and independence, large values will lead to an approximation of equal weighting, while small values will lead to aggressive weighting, giving a few models most of the weight. The shape parameters used in this study are summarized in table 1 and their calculation is described by Lorenz et al (2018) and in the supplement.
2.4. Diagnostics
The observational distance Di, is based on six diagnostics (see table 2). A diagnostic can be based on any CMIP5 output variable for which observations are available. The calculation of Di follows a straight-forward approach: (i) variable, region, time period, and season are selected, (ii) the mean (CLIM) or standard deviation (STD) over the time period is calculated, (iii) the point-to-point distance between model and the center of the observational spread is calculated, and finally (iv) the area-weighted root mean squared error is calculated over the selected region.
Table 2. Variables tested as diagnostics as well as selected diagnostics. Possible time aggregations are climatology (CLIM) and standard deviation (STD).
| Key | Name | Mask | Used diagnostics |
|---|---|---|---|
| pr | Precipitation | Sea | pr-CLIM |
| psl | Sea level pressure | — | |
| rnet | Surface downwelling net radiation | Sea | |
| rlds | Surface downwelling longwave radiation | Sea | rlds-STD |
| rlus | Surface upwelling longwave radiation | Sea | |
| rsds | Surface downwelling shortwave radiation | Sea | rsds-CLIM |
| rsus | Surface upwelling shortwave radiation | Sea | rsus-CLIM, rsus-STD |
| tas | Near-surface air temperature | Sea | tas-CLIM |
| tos | Sea surface temperature | Land |
To account for uncertainty in our knowledge of observed climate we use three observational estimates in the calculation of the point-to-point distance (iii). Several methods of combining these estimates and their influence on the weighting are investigated. Distances are tested with regard to each of the estimates individually as well as with regard to mean, median, and full spread. A detailed description of all steps and the different methods of combining observations can be found in the supplement.
The independence weighting is informed by diagnostics which can be based on any CMIP5 output variable which is available for all models. In practice, we use the same diagnostics as for the performance weighting. To compute the model distance Sij, the point-to-point difference (step (iii) above) is calculated between each model pair.
To select the most informative diagnostics, different combinations and numbers of diagnostics are tested and evaluated. The aim is to select diagnostics which are, on the one hand, relevant for the target and, on the other hand, add additional information to the already used diagnostics (Gleckler et al 2008, Lorenz et al 2018). We test a pool of variables (table 2) which we judge to be relevant for predicting our targets and for which observations are available. Indeed, the availability of observations of sufficient duration, spatial coverage, and quality is a considerable constraint for the pool of tested variables, particularly since we here aim at using multiple data sets in order to include observational uncertainty. Using the same approach as Lorenz et al (2018), we select six diagnostics, which is found to be a good number to differentiate between high and low performing models (performance tends to converge with an increasing number of diagnostics) while not being overconfident in a model's ability to reproduce observed climate (which becomes an issue with a low number of diagnostics) (Lorenz et al 2018).
2.5. Model-as-truth testing
A model-as-truth test (or perfect model test) picks each model from a multi-model ensemble in turn and treats it as the true representation of the climate system. Weights for the remaining models are computed using historical information from this perfect model as 'pseudo-observations'. This allows for an evaluation of the impact of the weighting in the future based on each model representing the truth once. Here this approach is used for two applications: (i) to estimate the ideal shape parameter for the performance weighting σD (as detailed in the supplement) and (ii) to evaluate the impact of the weighting on the skill of the future projections. As a measure for the skill we use the continuous ranked probability score (CRPS) as detailed in Hersbach (2000). For each perfect model the CRPS basically represents the mean absolute error between the distribution of all other models and the perfect model. We define the skill of the weighting as the relative change in CRPS in the end-of-century period:

3. Results
3.1. Summer temperature changes
We first calculate the optimized shape parameters (σD and σS) for all regions and periods. They deviate only slightly between mid-century and end-of-century and we therefore use the average over both periods in the computation of weights (table 1). Across all three SREX regions, the sigma values for temperature average to about σD = 0.6 and σS = 0.7, which is comparable to earlier work focusing on maximum summer temperature in North America (Lorenz et al 2018). In the four grid cell regions, the performance sigma values are about 50% higher than for the SREX regions due to the larger range of model-observation differences without spatial aggregation. Generally speaking, weighting based on smaller regions is less robust and, therefore, more likely to be overconfident. As a consequence the perfect model test correctly picks higher performance sigma values that lead to more evenly distributed weights and reduce overfitting.
Weighted and unweighted time-series of Mediterranean summer temperature are shown in figure 1. Models with less warming consistently get the lowest weights and, as a consequence, the weighted multi-model mean shifts upward by an additional 0.35 °C by the end of the century. The 25th percentile also shows a strong increase, moving above 5 °C warming for 2081–2100 (see also figure 2(a)). Since the increase in the 75th percentile is less distinctive, the weighting also leads to a reduction of the interquartile spread by almost 25%.
Figure 1. Mediterranean summer temperature anomaly (relative to 1995–2014) based on 79 models. Shown is the unweighted mean (thick gray line) and interquartile range (gray shading) as well as the weighted mean (thick red line) and interquartile range (red shading). The three best and three worst performing models are shown as thin red and purple lines, respectively. The observational spread is indicated in black, based on ERA-Interim, MERRA2, and E-OBS.
Download figure:
Standard image High-resolution imageFigure 2. (a) Weighted (colors) and unweighted (gray) summer mean temperature changes (relative to 1995–2014) in Europe (EUR), Northern Europe (NEU), the Mediterranean (MED), and Falun, Sweden (FAL). Shown is the mean, 50%, and 90% spread. (b) Strength of the weighting relative to the median weight for the same regions.
Download figure:
Standard image High-resolution imageFigure 2(a) shows temperature change distributions for the combined European domain, two SREX regions, and one of the grid cell regions. A summary of all regions can be found in figure S2(a) in the supplement. The effect of the weighting is generally smaller for the mid-century period. In the full European domain there is hardly any shift in the mean change, but a considerably reduction of the interquartile spread by about one quarter for the end-of-century period. Analyzing spatial differences reveals that the European domain seems to be a too large region to average over. The weighted mean is colder in the northern part and warmer in the southern part compared to the unweighted case consistent with the SREX regions described below. Aggregating over the entire domain cancels out most of this effect in the mean. In Northern Europe the interquartile spread widens by almost a third due to the weighting. This behavior is even stronger for the Falun grid cell with an increase by over 50%. Based on our diagnostics, it seems that models on both ends of the future temperature distribution get higher weights in NEU, indicating that a simple average and standard deviation might be slightly overconfident.
In Central Europe (figure S2(a)) neither mean nor spread are strongly affected by the weighting. This somewhat differs from findings by Vogel et al (2018), who constrain summer maximum temperature in this region to well below the ensemble mean, using the correlation between maximum temperature and precipitation as diagnostic. However, work from Stegehuis et al (2013) suggests that warming is underestimated by models in Northern and Central Europe and overestimated in the Mediterranean. We argue, therefore, that our approach might give a more robust estimate of the potential to narrow the uncertainty in this region, since it is based on a range of six diagnostics rather than on a single emergent constraint. It is, hence, not surprising that the Central European temperature distribution is not strongly affected be the weighting in our more conservative framework.
For the Mediterranean the weighting suggests that the unweighted multi-model mean strongly underestimates the potential warming in both periods. According to the weighted distribution, temperature increases of more than 2 °C are very likely already by the middle of the century when following RCP8.5. For the end of the century warming of over 5 °C compared to the 1995–2014 reference becomes increasingly likely.
Figure 2(b) shows that the best models receive up to tree times the median weight, except for the small grid cell regions Falun and Madrid with a maximum of 14× and 7× higher weights, respectively (see also figure S2(b)). The worst performing models in turn can get considerably lower weights more than 20× smaller than the median in several cases. Combining the results from figures 2(a) and (b) reveals that the effect of the weighting on the temperature distribution is a combination of the weighting strength and whether weights are correlated with simulated warming. The strong shift in the temperature distribution in the Mediterranean region is mainly driven by about 20% of the models which are heavily down-weighted for being far away from the observations in the historical period. For this specific region and target the majority of these models come from the GISS model family, which projects temperature changes on the lower end of the distribution. In Central Europe the weighting is equally strong but there is no clear clustering of weights for warmer or colder models so that there is hardly any effect on the temperature distribution. A list of all models included in the study and their corresponding weights in each of the regions can be found in figure S6 in the supplement.
3.2. The effect of observational uncertainty
The area-mean observational range for the Mediterranean (shown in black in figure 1) can cover large fractions of the interquartile model spread. This highlights the importance of accounting for observational uncertainty, particularly for diagnostics where many models lie within the observational spread. To investigate the effect of using multiple observational estimates we also calculate the weights based on each of the three used observational datasets separately. In most regions using only one dataset can lead to a shift in the mean which is not in line with the combined case (figure 3). This becomes even more important when considering smaller regions such as FAL, where using different observational estimates can lead to the weighting changes having different signs. Note that combining multiple datasets does not necessarily lead to a linear combination of the weighting effect. This can best be seen in the mean of NEU or in the 95th percentile of MED. We therefore stress the importance of using as many observational datasets as possible or feasible to best capture uncertainty in the observational estimates when evaluating historical model performance.
Figure 3. As figure 2(a) but only for 2081–2100 and also showing weighting based on each of the observational data sets individually.
Download figure:
Standard image High-resolution imageTo investigate the robustness of our approach to combine multiple observational datasets we also look into additional methods of combining the information from the three datasets (see supplement for a detailed description). As discussed in detail in section 4 one can even argue that the observations should also be weighted, but since the results from the different approaches tested are reasonably robust (figure S3), we limit ourselves to using the center of the observational spread here.
3.3. Summer precipitation changes
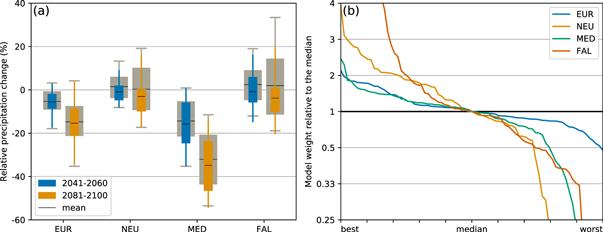
Precipitation changes are most notably affected by the weighting in Northern Europe (figure 4(a)): future precipitation increases are strongly constrained for both periods. This drives a reduction of the interquartile range by up to 50%. Similar to temperature, the effect on the precipitation distribution is mainly driven by a strong down-weighting of about 25% of models mainly from the CSIRO and IPSL families, which show a slight precipitation increase (figures 4(b) and S6). Looking into the absolute precipitation rather than the change reveals that the lower weighted models are predominantly dryer than the mean in the historical period and subsequently show a slightly stronger increase in precipitation than the mean under RCP8.5.
Figure 4. As figure 2 but for precipitation.
Download figure:
Standard image High-resolution imageIn the combined European domain as well as Central Europe, the weighting leads to a reduction in the uncertainty of the projections of about 20% in the middle of the century as the most prominent effect. Using precipitation observations as a constraint this potential of significantly reducing uncertainty in future precipitation changes was also found by, e.g. Zhang and Soden (2019). In the Mediterranean the weighted distribution indicates a tendency towards even dryer conditions than the unweighted mean. Together with the results from temperature shown in figure 2(a) this suggests that models with higher temperatures and associated stronger drying are more reliable based on their past performance.
3.4. Projection skill changes in model-as-truth tests
To evaluate the skill of the weighting approach we use the CRPS in model-as-truth experiments for the end of the century (2081–2100). Figure 5 shows the skill for three different cases: (i) weighing of the full ensemble, (ii) selecting a subset of the 10 best models (based on the same weights) with each model getting equal weight, and (iii) selecting a subset of the 10 best models where each models keeps its original weight.
Figure 5. Change in the continuous ranked probability score (CRPS) in a 'model-as-truth' setting for (left) temperature change and (right) precipitation change in the period 2081–2100 relative to 1995–2014.
Download figure:
Standard image High-resolution imageFor temperature in the European domain the median skill increases by almost 50% due to the weighting. In the three SREX regions the skill also increases, while there is hardly any increase in the grid cell region (figures 5(a) and S5(a)). It is noteworthy that the skill increase is also observable in regions where there is no obvious change in the temperature distribution (see, e.g. CEU in figure 2(a)). In the 'models are indistinguishable from the truth' paradigm (Sanderson and Knutti 2012) this can be interpreted as the observations representing one realization which does not lead to a strong weighting. But other realizations (represented by model 'pseudo-observations') can lead to a weighting which yields a skill increase.
For all regions there is also a chance that the skill decreases due to the weighting. This can happen if the perfect model has a very different response to future forcing compared to the other models, leading to the weighted multi-model ensemble moving further away from the 'truth'. This represents the possibility that weighting models based on the distance to the observations may have negative impact on the skill of the future projections. To minimize this risk of overconfidently weighting the projections and giving too narrow uncertainty estimates we select the performance shape parameter σD also based on a model-as-truth test. Therefore, the probability for a decrease in the skill is small when using the full ensemble.
Comparing this approach to picking only the 10 best models (unweighted or weighted), yields similar results for the median CRPS change and for the interquartile range. For most regions the median performance is even slightly better than for the full weighted ensemble. Crucially, however, picking only 10 members can perform considerably worse in the lower percentiles. Selecting a subset of models has a higher chance of overfitting and can lead to a reduction in the CRPS by more than 75% for temperature.
Depending on the question it might, therefore, be sufficient to only use a subset of the best models. The median skill of the 10 weighted members is better than using the full ensemble for all regions and sub-selection naturally leads to a highly reduced spread, which can be valuable for certain applications. However, to minimize the risk of making the projections worse it can be important to use the full weighted ensemble. This is particularly crucial for applications where worst-case scenarios are important, e.g. when the goal is to explore nonlinearities in impacts.
For precipitation the above considerations are even more important with the 5th percentile of the skill metric being reduced by 75% and more in many regions when picking only 10 models. For Sibiu and Madrid selecting only 10 models even leads to negative median skill (figure S5(b)). Using the full weighted ensemble does also not lead to significant skill increases, but at least limits the maximum CRPS decrease to about 50%.
In general, the model-as-truth tests show that weighting precipitation projections only leads to increased skill in reasonably large regions. In the largest region, the combined European domain hardly any increase in the median skill is found, which can be interpreted as the region being too large to apply a single weight per model. The highest skill increases are achieved in the Northern European region, with a median increase of about 40%.
4. Discussion, conclusions, and outlook
This work applies a weighting approach, which accounts for performance and independence, to temperature and precipitation projections in Europe. We show that weighting generally leads to an increase in the median projection skill, which can reach up to 50%. This result depends strongly on the region size, with smaller regions showing less increase and even a decrease in one extreme case. It is, therefore, evident, that some degree of spatial aggregation is needed in order to produce robust weighting. In turn, weighting leads to temperature and precipitation changes with opposing signs in northern and southern Europe, which cancel each other out when aggregating the full European region. Choosing the right region size is therefore crucial for producing reliable and physically meaningful results.
The European SREX regions are found to be such regions. For temperature the strongest effect of weighing is found in the Mediterranean, with a warming of over 2 °C (compared to 1995–2014) becoming very likely already by the middle of the century. For precipitation a large reduction in spread is evident in the Northern European SREX region. Our results reveal that a future decrease in Northern European precipitation is more likely than indicated by the unweighted multi-model mean with models which show an increase consistently getting the lowest weights.
Several important questions are not addressed here and will be investigated in future work: How does the number of diagnostics affect the weights and therefore the skill? Is there a subset of diagnostics which have predictive skill for many different targets? What is the impact of the diagnostic period length and the lead time? Is there an influence of model resolution on the ideal region size or is it rather driven by the homogeneity of the region? Further, the effect of the independence weighting is not discussed in detail here. It has been argued that using a measure for model inter-dependence is important in so-called 'ensembles of opportunity' such as CMIP5, which are not designed to represent independent realizations of the climate system (e.g. Abramowitz et al 2019). An in-depth investigation of the independence weighting, e.g. by consecutively adding more and more initial condition members of the same model, is also currently in progress. Accounting for larger initial condition ensembles will become increasingly important in light of the upcoming CMIP6, for which several models with 20 and more members are planned (WCRP 2019).
To inform the weighting, we propose a novel approach for including observational uncertainty and apply different methods to account for the observational spread. In general, using only one observational estimate as ground truth does not account for the fact that datasets derived from observations represent reality with uncertainty. In the case of in situ measurements uncertainty arises from measuring itself and the subsequent processing into a gridded product. Specific sources of uncertainties are, for instance, the accuracy of the sensor, data gaps, and the gridding and interpolation procedures used. To account for the parametric uncertainties of the underlying procedures increasingly multiple realizations are constructed, such as the E-OBS or HadCRUT4 ensembles (Morice et al 2012, Cornes et al 2018). Satellite remote sensing such as the radiation measurements from the CERES instruments provide another important source of information for climate science. To derive relevant atmospheric variables on a regular grid from the raw measurements, physical theory and complex modeling as well as calibration procedures are necessary, which are subject to uncertainty. Finally, reanalysis datasets use process-based numerical models in their estimation and therefore additional uncertainties arise, for example, initial condition uncertainty and boundary condition uncertainty.
To account for these uncertainties we use three structurally different observational estimates and apply different methods to combine them. Our results show that including observational uncertainty leads to more robust results, mostly independent of the used method and therefore underline the importance of using multiple observational datasets. However, while the proposed weighting approach takes into consideration that climate models are not independent from each other, we still imply 'observational democracy', assuming that all observational estimates are independently constructed. Further research is needed to account also for inter-dependence between observational estimates which could then potentially allow the combined use of parametric and structural ensembles.
The selection of variables, regions, and time periods in this work is guided by a coordinated effort to compare different methods to constrain future projections of European climate, which is carried out in the frame of the EUCP project (Hewitt and Lowe 2018). In light of the upcoming sixth assessment report (AR6) of the IPCC and with the new generation of CMIP6 models becoming available and the connected increase in initial condition members a broad discourse about ways to combine multi-model ensembles will become even more important in order to produce the best possible estimates of future changes.
Acknowledgments
The authors thank Anna L Merrifield for helpful discussions and comments. The EUCP project is funded by the European Commission through the Horizon 2020 Programme for Research and Innovation: Grant Agreement 776613. Ruth Lorenz was funded by the European Union's Horizon 2020 Research and Innovation program: Grant Agreement 641816 (CRESCENDO). We thank ECMWF for providing ERA-Interim, NASA for providing MERRA2 and the CERES EBAF-Surface Product, the EU-FP6 project UERRA (http://uerra.eu) and the Copernicus Climate Change Service, and the data providers in the ECA&D project (https://ecad.eu) for providing E-OBS. We acknowledge the World Climate Research Programme's Working Group on Coupled Modeling, which is responsible for CMIP, and we thank the climate modeling groups for producing and making available their model output. For CMIP the US Department of Energy's Program for Climate Model Diagnosis and Intercomparison provides coordinating support and led development of software infrastructure in partnership with the Global Organization for Earth System Science Portals. The analysis was carried out in Python, the code is available via GitHub (https://github.com/lukasbrunner/ClimWIP) under a GPLv3. We thank all contributors to the numerous Python packages which were crucial for this work, in particular the xarray project (http://xarray.pydata.org).
The authors thank two anonymous reviewers for their helpful comments on this manuscript.
Data availability statement
The data that support the findings of this study are openly available at the links listed below. ERA-Interim is available at https://apps.ecmwf.int/datasets/data/interim-full-moda/, MERRA2 at https://gmao.gsfc.nasa.gov/reanalysis/MERRA-2, the CERES EBAF-Surface Product at https://ceres.larc.nasa.gov/products.php?product=EBAF-Surface, E-OBS at https://ecad.eu, and CMIP data at https://esgf.llnl.gov/.