File:Erays.png
From Wikimedia Commons, the free media repository
Jump to navigation
Jump to search

Size of this preview: 800 × 400 pixels. Other resolutions: 320 × 160 pixels | 640 × 320 pixels | 1,000 × 500 pixels.
Original file (1,000 × 500 pixels, file size: 17 KB, MIME type: image/png)
File information
Structured data
Captions
Captions
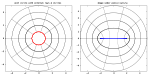
polar coordinate system and mapping from the complement (exterior) of the closed unit disk to the complement of the filled Julia set for c=-2
Summary
[edit]| DescriptionErays.png |
English: Polar coordinate system and mapping from the complement (exterior) of the closed unit disk to the complement of the filled Julia set for
 . .Polski: Układ współrzędnych biegunowych oraz funkcja odwzorowująca dopełnienie dysku jednostkowego na dopełnienie zbioru Julia. |
|||||
| Date | 4 November 2008 (original upload date) | |||||
| Source | Own work by uploader in Maxima and Gnuplot with help of many people (see references) | |||||
| Author | Adam majewski | |||||
| Other versions |
|
|||||
| Source code InfoField | Created using Maxima.
R_max: 5;
R_min: 1;
dR: R_max - R_min;
psi(w) := w+1/w;
NmbrOfRays: 10;
iMax: 100; /* number of points to draw */
GiveCirclePoint(t) := R*%e^(%i*t*2*%pi); /* gives point of unit circle for angle t in turns */
GiveWRayPoint(R) := R*%e^(%i*tRay*2*%pi); /* gives point of external ray for radius R and angle tRay in turns */
/* f_0 plane = W-plane */
/* Unit circle */
R: 1;
circle_angles: makelist(i/(10*iMax), i, 0, 10*iMax-1); /* more angles = more points */
CirclePoints: map(GiveCirclePoint, circle_angles);
/* External circles */
circle_radii: makelist(R_min+i, i, 1, dR);
WCirclesPoints: [];
for R in circle_radii do
WCirclesPoints: append(WCirclesPoints, map(GiveCirclePoint, circle_angles));
/* External W rays */
ray_radii: makelist(R_min+dR*i/iMax, i, 0, iMax);
ray_angles: makelist(i/NmbrOfRays, i, 0, NmbrOfRays-1);
WRaysPoints: [];
for tRay in ray_angles do
WRaysPoints: append(WRaysPoints, map(GiveWRayPoint, ray_radii));
/* f_c plane = Z plane = dynamic plane */
/* external Z rays */
ZRaysPoints: map(psi, WRaysPoints);
/* Julia set points */
JuliaPoints: map(psi, CirclePoints);
Equipotentials: map(psi, WCirclesPoints);
/* Mario Rodríguez Riotorto (http://www.telefonica.net/web2/biomates/maxima/gpdraw/index.html) */
load(draw);
draw(
file_name = "erays",
pic_width = 1000,
pic_height = 500,
terminal = 'png,
columns = 2,
gr2d(
title = " unit circle with external rays & circles ",
point_type = filled_circle,
points_joined = true,
point_size = 0.34,
color = red,
points(map(realpart, CirclePoints),map(imagpart, CirclePoints)),
points_joined = false,
color = black,
points(map(realpart, WRaysPoints), map(imagpart, WRaysPoints)),
points(map(realpart, WCirclesPoints), map(imagpart, WCirclesPoints))
),
gr2d(
title = "Image under psi(w):=w+1/w; ",
points_joined = true,
point_type = filled_circle,
point_size = 0.34,
color = blue,
points(map(realpart, JuliaPoints),map(imagpart, JuliaPoints)),
points_joined = false,
color = black,
points(map(realpart, ZRaysPoints),map(imagpart, ZRaysPoints)),
points(map(realpart, Equipotentials),map(imagpart, Equipotentials))
)
);
|
Long description
[edit]Here are two diagrams:
- on the left is dynamical plane for
- on the right is dynamical plane for
On left diagram one can see:
- Julia set (unit circle) in red
- concentric circles outside unit circle
- external rays (radial lines outside unit circle)
Right diagram is image of left diagram under function 


For 

It is:
- a simplest case for analysis,
- only one case when formula for computing
is known (explicit Riemann mapping).

- red unit circle
to blue line segment
(Julia sets)
- concentric circles to ellipses (equipotential lines)
- rays of unit circle to hyperbolas (external rays)
Licensing
[edit]I, the copyright holder of this work, hereby publish it under the following licenses:
This file is licensed under the Creative Commons Attribution-Share Alike 3.0 Unported license.
- You are free:
- to share – to copy, distribute and transmit the work
- to remix – to adapt the work
- Under the following conditions:
- attribution – You must give appropriate credit, provide a link to the license, and indicate if changes were made. You may do so in any reasonable manner, but not in any way that suggests the licensor endorses you or your use.
- share alike – If you remix, transform, or build upon the material, you must distribute your contributions under the same or compatible license as the original.

|
Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or any later version published by the Free Software Foundation; with no Invariant Sections, no Front-Cover Texts, and no Back-Cover Texts. A copy of the license is included in the section entitled GNU Free Documentation License.http://www.gnu.org/copyleft/fdl.htmlGFDLGNU Free Documentation Licensetruetrue |
You may select the license of your choice.
References
[edit]- ↑ Peitgen, Heinz-Otto; Richter Peter (1986) The Beauty of Fractals, Heidelberg: Springer-Verlag ISBN: 0-387-15851-0.
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 14:50, 4 November 2008 |  | 1,000 × 500 (17 KB) | Soul windsurfer (talk | contribs) | {{Information |Description= More angles |Source= |Date= |Author= |Permission= |other_versions= }} |
| 14:30, 4 November 2008 |  | 1,000 × 500 (12 KB) | Soul windsurfer (talk | contribs) | {{Information |Description={{en|1=polar coordinate system and mapping from the complement (exterior) of the closed unit disk to the complement of the filled Julia set for c=-2}} {{pl|1=Układ współrzędnych biegunowych oraz funkcja odwzorowująca dope |
You cannot overwrite this file.
File usage on Commons
The following page uses this file: