Pubblico le nostre soluzioni
ai tre quesiti
Gli impegni a volte si accavallano causando dei rinvii ma, eccoci qua!
Quesito 1, ricerca di un Codice di accesso
Hanno saputo elaborare le chiavi, per la classe prima: Antonio, Sara, Elena, Davide, Paola, Andrea, Roberta, Aurora, Marta C., Martina, Yuri, Elisa, Valentina, Margherita.
Michele ha lavorato con la cugina Elisa, di terza, la quale ha fatto un ragionamento da terza che Michele ha, giustamente, faticato a seguire.
Tutti trovano la soluzione più o meno con lo stesso ragionamento: considerano cioè le chiavi una per una e, suppongo per tentativi, trovano le corrette cifre che soddisfano le chiavi stesse. Le risposte sono quasi tutte simili a questa:
Per risolvere il quesito ho iniziato seguendo la prima chiave: “il quinto numero sommato al terzo da come risultato 14”. [C’è pure chi ha iniziato dalla chiave 4]. Quindi ho provato con 6, come terzo numero, e con 8, come quinto numero. A quel punto non potevo decifrare la seconda e la terza chiave e sono passata alla quarta: “il secondo numero sommato al terzo dà come risultato 10”. Quindi, come secondo numero, ho potuto mettere 4, perché il terzo numero era 6 e sono tornata alla seconda chiave: “il quarto numero è il secondo aumentato di 1”. Ho messo 5 come quarto numero perché il secondo numero era 4.
Successivamente sono passata alla terza chiave: “il primo numero è inferiore di uno al doppio del secondo ”quindi come primo numero ho messo 7 perché: 4 (secondo n°)*2-1=7 e infine ho sommato tutte le cifre del numero, come scritto nella chiave 5, e ho ottenuto 30.
Le cifre della combinazione sono: 74658
Per la terza hanno risolto: Alessia, Antonella, Elisa, Miriam, Gian Franco, Giuseppe P., Antonio, Erika.
I ragazzi di terza (quasi tutti) già si aiutano con le lettere per impostare le soluzioni alle chiavi.
In generale tuttavia seguono poi il ragionamento aritmetico visto sopra. Qualcuno precisa però di aver ipotizzato i numeri che rispondessero alle chiavi per poi arrivare alle corrette scelte: “ci sono arrivata un po’ per tentativi e un po’ con ragionamenti, aiutandomi con le lettere: a, b, c, d, e sono i numeri … sono arrivata alla password dell’uomo: 74658”
Alessia ha invece saputo già sfruttare le poche basi per ora gettate qua e là, solo lavorando in una diversa ottica, su calcolo letterale ed equazioni. Questa la sua soluzione:
Il primo numero lo scrivo come "a", il secondo "b", il terzo "c", il quarto "d" e infine l'ultimo "e".
Per prima cosa mi concentro sull'ultima "chiave" scrivendo: 30=a+b+c+d+e
Poi guardo gli indizi che mi comunicano le altre "chiavi", soprattutto la prima che dice che la somma del terzo e del quinto è uguale a 14, quindi scrivo:
c+e=14
Successivamente da 30 sottraggo 14 e scrivo:
30-14 = a+b+d = 16
Ricontrollando le "chiavi" e la mia mezza soluzione decido di unire la seconda "chiave", che dice che il quarto è il secondo aumentato di uno, cioè d=b+1,
e la terza "chiave", che dice che il primo numero è inferiore di uno del doppio del secondo cioè a=2b-1,
addizionando la "a" e la "d" scrivendo così:
2b-1 + b+1 = 3b
Ora a+b+d si può scrivere: 3b+b=4b
Completando la mia soluzione scrivo: 4b=16
Ora sono in grado di conoscere il valore di "b": 16/4= 4
Quindi:
a= 2b-1=2*4-1=7
b=4
c=10-b=10-4=6
d=b+1=4+1=5
e=14-c=14-6=8
7+4+6+5+8=30
La sequenza è: 7-4-6-5-8
Beh, la prof ha espresso soddisfazione  Si è complimentata con Alessia e: ”vedi, quasi senza accorgerti hai usato calcolo letterale ed equazioni!”
Si è complimentata con Alessia e: ”vedi, quasi senza accorgerti hai usato calcolo letterale ed equazioni!”
Elisa ha risolto anche lei con equazioni, ma in maniera per noi ancora troppo astratta. In realtà dice di aver avuto l’aiuto del fratello. (E figuriamoci, pretendeva poi di spiegare al cuginetto  ) - Eli, come vedi sorrido, noi abbiamo già chiarito tutto, lo sai. Tu hai fatto del tuo meglio.
) - Eli, come vedi sorrido, noi abbiamo già chiarito tutto, lo sai. Tu hai fatto del tuo meglio.
Veniamo al
Quesito 2
Si chiedeva in pratica utilizzando 21 fiammiferi, di costruire i diversi triangoli aventi perimetro di 21 u
Per la prima risolvono correttamente: Paola, Andrea, Roberta, Antonio, Sara, Aurora (con qualche errore nelle misure dei lati), Valentina, Yuri (poco chiaro nelle conclusioni, giro di parole di troppo, si fatica ad aver ben presente i triangoli) e Martina (con qualche errore).
I 12 triangoli trovati hanno le seguenti misure dei lati:
(10, 10, 1) (10, 9, 2) (10, 8, 3) (10, 7, 4) (10, 6, 5) (9, 9, 3) (9, 8, 4) (9, 7, 5) (9, 6, 6) (8, 8, 5) (8, 7, 6) (7, 7, 7)
Ragazzi, come vedete ho scritto le misure in un certo ordine per suggerirvi quale poteva essere un criterio per non perdersi, per non avere ripetizioni né sviste.
Solo qualcuno ha seguito un criterio per trovare tutti i triangoli. In questo momento ricordo solo Roberta che:
“ho riflettuto su quali tipi di triangoli conosco: equilatero, isoscele e scaleno.
Quindi ho calcolato quanti fiammiferi andavano disposti nei lati di ogni triangolo:
Equilatero, lati tutti uguali: 7 in ogni lato
Isoscele, due lati uguali: 6 , 8, 9, 10 fiammiferi per i lati uguali.
Scaleno, tutti i lati diversi: 5+6+10; 5+7+9; 6+7+8; 7+4+10; 8+4+9; 8+3+10; 9+2+10.”
Qualcun altro mi ha detto... un qualche criterio che ora non ricordo. E, infine, Paola ha precisato che: ovviamente la misura di un lato deve essere inferiore alla somma degli altri due lati. Bene!
Andrea, Paola, Roberta e Aurora, seppure con le dritte dell’insegnante, hanno realizzato le costruzioni di tutti i triangoli con GeoGebra. Bravi!
Ecco qualche immagine d’esempio:


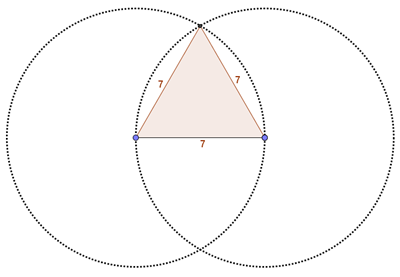
Ragazzi, ho visualizzato io le circonferenze (e le ho tratteggiate – imparare!) per mostrare che avete lavorato bene 
Per la terza risolvono: Alessia, Antonella (non hai costruito su GeoGebra!), Miriam, Gian Franco, Giuseppe P., Erika.
Dal richiamo ad Antonella si deduce che gli altri hanno realizzato le costruzioni (Giuseppe è stato aiutato ma, bravo, Giu’!, Miriam ha usato lo slider per controllare la visualizzazione dei vari triangoli).
Alessia, ancora una volta ha voluto sorprenderci 
Proprio perché c’è la sorpresa, ho caricato l’applet del suo lavoro.
Ehm ... Alessia è tutt’altro che un’alunna degenere, ma ha rischiato di esserlo perché, ad una mia osservazione, anziché migliorare, peggiorava le cose! Ok, per sfinimento ho corretto io un particolare...
Clic sull’immagine per visualizzare la costruzione

Infine, il
Quesito 3 la carta coperta

La risposta corretta è stata data, per la prima, da: Antonio, Elena, Aurora, Marta C., Andrea, Paola, Davide, Roberta, Elisa, Yuri, Valentina, Margherita, Sara e Martina.
Qualcuno ha scordato di precisare il seme della carta, la soluzione è stato data in generale con la spiegazione:
La carta mancante è 8 di fiori. Fiori perché non è ancora stato usato quel simbolo, e poi perché 3 + 5 = 8 e 5 + 8 = 13.
Oppure con la variante: la carta mancante è 8 di fiori perché la differenza tra il n° 5 e il n° 13 è 8. Per averne la prova ho riflettuto sulla differenza tra il 3 e l' 8 ed è proprio 5.
Aurora e Valentina aggiungono, l’una: “... ritorniamo al famoso Fibonacci” e l’altra: “in queste carte si è usato il metodo di Fibonacci, ecco qui il metodo: 1, 1, 2, 3, 5, 8, 13....e poi tanti altri, ovviamente, perché i numeri sono infiniti.” (!)
Aurora, mi racconta: “quando ho trovato la carta, babbo mi ha detto di andare a guardare un volume dell’enciclopedia rossa che ho in camera e ho trovato Fibonacci. Perché ne avevamo parlato con il Sistema di numerazione decimale [di Fibonacci, non della successione]”
Boh, io non ho capito bene come abbia trovato!
Valentina mi riferisce di aver digitato su Google, una volta scoperta la carta, poiché si parlava di qualcosa di famoso, la sequenza 3, 5, 8, 13 e ... ha trovato anche lei Fibonacci! Mi dice di aver pensato anche al Liber Abaci ma mica ho capito 
Per la terza hanno risposto: Alessia, Antonella, Miriam, Gian Franco, Giuseppe P., Erika, Elisa, Antonio.
Miriam scrive:
La sequenza logica che mi ha permesso di scoprire la terza carta, è la sequenza di Fibonacci ("scoperta" l'anno scorso a scuola, e rivista nel libro di Dan Brown "Il Codice da Vinci")
Essa è: 1 1 2 3 5 8 13 21 ........
E dice che ogni numero è sempre uguale alla somma dei due numeri che lo precedono; 1+1= 2, 1+2= 3, 2+3= 5, 3+5= 8 ecc..
Perciò, basandomi su questa sequenza, mi è venuto semplice trovare la carta mancante: è un 8 di fiori.
Anche Gian Franco, Antonella (che si è documentata dopo mia richiesta, brava), Alessia, Erika, Elisa hanno riconosciuto la successione di Fibonacci. Giuseppe fa grandi progressi nella soluzione dei quesiti.
FINE!
Come sempre se ho scordato qualcosa o qualcuno, segnalate.
BRAVI, tutti coloro che hanno lavorato.
Non mi resta che raccomandare di tenersi pronti per i nuovi quesiti dal prof Davide.