八皇后问题:修订间差异
小 機器人 修改: pl:Problem ośmiu hetmanów; 細部更改 |
|||
| (未显示48个用户的72个中间版本) | |||
| 第1行: | 第1行: | ||
{{Chess diagram |
{{Chess diagram |
||
| tright |
| tright |
||
| |
| |
||
|= |
|||
|__|__|__|__|__|ql|__|__ |
|||
|__|__|__|ql|__|__|__|__ |
|||
|__|__|__|__|__|__|ql|__ |
|||
|ql|__|__|__|__|__|__|__ |
|||
|__|__|__|__|__|__|__|ql |
|||
|__|ql|__|__|__|__|__|__ |
|||
|__|__|__|__|ql|__|__|__ |
|||
|__|__|ql|__|__|__|__|__ |
|||
|八皇后问题的一 |
|八皇后问题的唯一对称解(不包括旋转和反射变换) |
||
}} |
}} |
||
'''八皇后问题'''是一个以[[国际象棋]]为背景的问题:如何能够在8×8的国际象棋棋盘上放置八个[[后 (国际象棋)|皇后]],使得任何一个皇后都无法直接吃掉其他的皇后?为了达到此目的,任两个皇后都不能处于同一条横行、纵行或斜线上。八皇后问题可以推广为更一般的'''''n''皇后摆放问题''':这时棋盘的大小变为''n''×''n'',而皇后个数也变成''n''。[[当且仅当]]''n'' = 1或''n'' ≥ 4时问题有解<ref>Watkins, John J. (2004). ''Across the Board: The Mathematics of Chess Problems''. Princeton: Princeton University Press. ISBN 0-691-11503-6</ref>。 |
|||
'''八皇后问题'''是一个以[[国际象棋]]为背景的问题:如何能够在 8×8 的国际象棋棋盘上放置八个[[后 (国际象棋)|皇后]],使得任何一个皇后都无法直接吃掉其他的皇后?为了达到此目的,任两个皇后都不能处于同一条横行、纵行或斜线上。八皇后问题可以推广为更一般的'''''n''皇后摆放问题''':这时棋盘的大小变为''n''×''n'',而皇后个数也变成''n''。当且仅当 ''n'' = 1 或 ''n'' ≥ 4 时问题有解。 |
|||
== 历史 == |
== 历史 == |
||
八皇后问题最早是由 |
八皇后问题最早是由西洋棋棋手[[马克斯·贝瑟尔]](Max Bezzel)于1848年提出。第一个解在1850年由弗朗兹·诺克(Franz Nauck)给出。并且将其推广为更一般的''n''皇后摆放问题。诺克也是首先将问题推广到更一般的''n''皇后摆放问题的人之一。 |
||
在此之后,陆续有[[数学家]]对其进行研究,其中包括[[卡尔·弗里德里希·高斯|高斯]]和[[格奥尔格·康托尔|康托]],1874年,S.冈德尔提出了一个通过[[行列式]]来求解的方法<ref name="rouse_ball_1960">{{tsl|en|W. W. Rouse Ball||W. W. Rouse Ball}} (1960) ''The Eight Queens Problem'', in Mathematical Recreations and Essays, Macmillan, New York, pp 165-171.</ref>,这个方法后来又被[[詹姆斯·维特布莱德·李·格莱舍|J.W.L.格莱舍]]加以改进。 |
|||
[[艾兹格·迪杰斯特拉]]在1972年用这个问题为例来说明他所谓[[结构性编程]]的能力<sup>[[#References|2]]</sup>。 |
|||
1972年,[[艾兹格·迪杰斯特拉]]用这个问题为例来说明他所谓[[结构化编程]]的能力<ref>[[奧利-約翰·達爾]], [[艾兹赫尔·戴克斯特拉]], [[東尼·霍爾]] ''Structured Programming'', Academic Press, London, 1972 ISBN 0-12-200550-3 see pp 72-82 for Dijkstra's solution of the 8 Queens problem.</ref>。他对[[深度优先搜索]][[回溯法|回溯算法]]有着非常详尽的描述<sup>[[#參考資料|2]]</sup>。 |
|||
八皇后问题出现在1990年代初期的著名电子游戏[[第七访客]]中。 |
|||
八皇后问题在1990年代初期的著名电子游戏《[[第七访客]]》和[[任天堂DS|NDS]]平台的著名电子游戏《[[雷顿教授与不可思议的小镇]]》中都有出现。 |
|||
== 八皇后問題的解 == |
|||
== 解题方法 == |
|||
八皇后问题一共有 92 个'''互不相同'''的解。如果将旋转和对称的解归为一种的话,则一共有12个独立解,具体如下: |
|||
八个皇后在8x8棋盘上共有4,426,165,368([[组合|<sub>64</sub>C<sub>8</sub>]])种摆放方法,但只有92个'''可行(皇后間互不攻擊)'''的解。如果将旋转和对称的解归为一种的话,则一共有12个独立解,具体如下: |
|||
{{multicol}} |
|||
<table> |
|||
{{Chess diagram small |
|||
<tr> |
|||
| tnone |
|||
<td> |
|||
{{Chess diagram|= |
|||
| tright |
|||
| |
| |
||
|= |
|||
|__|__|__|ql|__|__|__|__ |
|||
|__|ql|__|__|__|__|__|__ |
|||
|__|__|__|__|__|__|ql|__ |
|||
|__|__|ql|__|__|__|__|__ |
|||
|__|__|__|__|__|ql|__|__ |
|||
|__|__|__|__|__|__|__|ql |
|||
|__|__|__|__|ql|__|__|__ |
|||
|ql|__|__|__|__|__|__|__ |
|||
|独立解1 |
|独立解1 |
||
}} |
}} |
||
{{multicol-break}} |
|||
</td> |
|||
{{Chess diagram small |
|||
<td> |
|||
| tnone |
|||
{{Chess diagram|= |
|||
| tright |
|||
| |
| |
||
|= |
|||
|__|__|__|__|ql|__|__|__ |
|||
|__|ql|__|__|__|__|__|__ |
|||
|__|__|__|ql|__|__|__|__ |
|||
|__|__|__|__|__|__|ql|__ |
|||
|__|__|ql|__|__|__|__|__ |
|||
|__|__|__|__|__|__|__|ql |
|||
|__|__|__|__|__|ql|__|__ |
|||
|ql|__|__|__|__|__|__|__ |
|||
|独立解2 |
|独立解2 |
||
}} |
}} |
||
{{multicol-break}} |
|||
</td> |
|||
{{Chess diagram small |
|||
<td> |
|||
| tnone |
|||
{{Chess diagram|= |
|||
| tright |
|||
| |
| |
||
|= |
|||
|__|__|__|__|ql|__|__|__ |
|||
|__|__|__|__|__|__|ql|__ |
|||
|ql|__|__|__|__|__|__|__ |
|||
|__|__|ql|__|__|__|__|__ |
|||
|__|__|__|__|__|__|__|ql |
|||
|__|__|__|__|__|ql|__|__ |
|||
|__|__|__|ql|__|__|__|__ |
|||
|__|ql|__|__|__|__|__|__ |
|||
|独立解3 |
|独立解3 |
||
}} |
}} |
||
{{multicol-break}} |
|||
</td> |
|||
{{Chess diagram small |
|||
</tr> |
|||
| tnone |
|||
<tr> |
|||
<td> |
|||
{{Chess diagram|= |
|||
| tright |
|||
| |
| |
||
|= |
|||
|__|__|__|ql|__|__|__|__ |
|||
|__|__|__|__|__|ql|__|__ |
|||
|__|__|__|__|__|__|__|ql |
|||
|__|__|ql|__|__|__|__|__ |
|||
|ql|__|__|__|__|__|__|__ |
|||
|__|__|__|__|__|__|ql|__ |
|||
|__|__|__|__|ql|__|__|__ |
|||
|__|ql|__|__|__|__|__|__ |
|||
|独立解4 |
|独立解4 |
||
}} |
}} |
||
{{multicol-end}} |
|||
</td> |
|||
{{multicol}} |
|||
<td> |
|||
{{Chess diagram |
{{Chess diagram small |
||
| |
| tnone |
||
| |
| |
||
|= |
|||
|__|__|ql|__|__|__|__|__ |
|||
|__|__|__|__|__|ql|__|__ |
|||
|__|__|__|__|__|__|__|ql |
|||
|ql|__|__|__|__|__|__|__ |
|||
|__|__|__|ql|__|__|__|__ |
|||
|__|__|__|__|__|__|ql|__ |
|||
|__|__|__|__|ql|__|__|__ |
|||
|__|ql|__|__|__|__|__|__ |
|||
|独立解5 |
|独立解5 |
||
}} |
}} |
||
{{multicol-break}} |
|||
</td> |
|||
{{Chess diagram small |
|||
<td> |
|||
| tnone |
|||
{{Chess diagram|= |
|||
| tright |
|||
| |
| |
||
|= |
|||
|__|__|__|__|ql|__|__|__ |
|||
|__|__|ql|__|__|__|__|__ |
|||
|__|__|__|__|__|__|__|ql |
|||
|__|__|__|ql|__|__|__|__ |
|||
|__|__|__|__|__|__|ql|__ |
|||
|ql|__|__|__|__|__|__|__ |
|||
|__|__|__|__|__|ql|__|__ |
|||
|__|ql|__|__|__|__|__|__ |
|||
|独立解6 |
|独立解6 |
||
}} |
}} |
||
{{multicol-break}} |
|||
</td> |
|||
{{Chess diagram small |
|||
</tr> |
|||
| tnone |
|||
<tr> |
|||
<td> |
|||
{{Chess diagram|= |
|||
| tright |
|||
| |
| |
||
|= |
|||
|__|__|__|__|ql|__|__|__ |
|||
|__|__|__|__|__|__|ql|__ |
|||
|__|__|__|ql|__|__|__|__ |
|||
|ql|__|__|__|__|__|__|__ |
|||
|__|__|ql|__|__|__|__|__ |
|||
|__|__|__|__|__|__|__|ql |
|||
|__|__|__|__|__|ql|__|__ |
|||
|__|ql|__|__|__|__|__|__ |
|||
|独立解7 |
|独立解7 |
||
}} |
}} |
||
{{multicol-break}} |
|||
</td> |
|||
{{Chess diagram small |
|||
<td> |
|||
| tnone |
|||
{{Chess diagram|= |
|||
| tright |
|||
| |
| |
||
|= |
|||
|__|__|__|ql|__|__|__|__ |
|||
|ql|__|__|__|__|__|__|__ |
|||
|__|__|__|__|ql|__|__|__ |
|||
|__|__|__|__|__|__|__|ql |
|||
|__|__|__|__|__|ql|__|__ |
|||
|__|__|ql|__|__|__|__|__ |
|||
|__|__|__|__|__|__|ql|__ |
|||
|__|ql|__|__|__|__|__|__ |
|||
|独立解8 |
|独立解8 |
||
}} |
}} |
||
{{multicol-end}} |
|||
</td> |
|||
{{multicol}} |
|||
<td> |
|||
{{Chess diagram |
{{Chess diagram small |
||
| |
| tnone |
||
| |
| |
||
|= |
|||
|__|__|ql|__|__|__|__|__ |
|||
|__|__|__|__|__|ql|__|__ |
|||
|__|__|__|ql|__|__|__|__ |
|||
|ql|__|__|__|__|__|__|__ |
|||
|__|__|__|__|__|__|__|ql |
|||
|__|__|__|__|ql|__|__|__ |
|||
|__|__|__|__|__|__|ql|__ |
|||
|__|ql|__|__|__|__|__|__ |
|||
|独立解9 |
|独立解9 |
||
}} |
}} |
||
{{multicol-break}} |
|||
</td> |
|||
{{Chess diagram small |
|||
</tr> |
|||
| tnone |
|||
<tr> |
|||
<td> |
|||
{{Chess diagram|= |
|||
| tright |
|||
| |
| |
||
|= |
|||
|__|__|__|__|__|ql|__|__ |
|||
|__|__|__|ql|__|__|__|__ |
|||
|__|__|__|__|__|__|ql|__ |
|||
|ql|__|__|__|__|__|__|__ |
|||
|__|__|__|__|__|__|__|ql |
|||
|__|ql|__|__|__|__|__|__ |
|||
|__|__|__|__|ql|__|__|__ |
|||
|__|__|ql|__|__|__|__|__ |
|||
|独立解10 |
|独立解10 |
||
}} |
}} |
||
{{multicol-break}} |
|||
</td> |
|||
{{Chess diagram small |
|||
<td> |
|||
| tnone |
|||
{{Chess diagram|= |
|||
| tright |
|||
| |
| |
||
|= |
|||
|__|__|__|__|__|ql|__|__ |
|||
|__|ql|__|__|__|__|__|__ |
|||
|__|__|__|__|__|__|ql|__ |
|||
|ql|__|__|__|__|__|__|__ |
|||
|__|__|__|ql|__|__|__|__ |
|||
|__|__|__|__|__|__|__|ql |
|||
|__|__|__|__|ql|__|__|__ |
|||
|__|__|ql|__|__|__|__|__ |
|||
|独立解11 |
|独立解11 |
||
}} |
}} |
||
{{multicol-break}} |
|||
</td> |
|||
{{Chess diagram small |
|||
<td> |
|||
| tnone |
|||
{{Chess diagram|= |
|||
| tright |
|||
| |
| |
||
|= |
|||
|__|__|__|ql|__|__|__|__ |
|||
|__|__|__|__|__|__|ql|__ |
|||
|ql|__|__|__|__|__|__|__ |
|||
|__|__|__|__|__|__|__|ql |
|||
|__|__|__|__|ql|__|__|__ |
|||
|__|ql|__|__|__|__|__|__ |
|||
|__|__|__|__|__|ql|__|__ |
|||
|__|__|ql|__|__|__|__|__ |
|||
|独立解12 |
|独立解12 |
||
}} |
}} |
||
{{multicol-end}} |
|||
</td> |
|||
</tr> |
|||
</table> |
|||
== 解的个数 == |
== 解的个数 == |
||
下表给出了 |
下表给出了''n''皇后问题的解的个数包括独立解U{{OEIS|id=A002562}}以及可行解D{{OEIS|id=A000170}}的个数: |
||
{| class="wikitable" |
{| class="wikitable" |
||
! |
!''n'' |
||
!1 |
|||
!style="padding: 0em .5em;"|1 |
|||
!2 |
|||
!style="padding: 0em .5em;"|2 |
|||
!3 |
|||
!style="padding: 0em .5em;"|3 |
|||
!4 |
|||
!style="padding: 0em .5em;"|4 |
|||
!5 |
|||
!style="padding: 0em .5em;"|5 |
|||
!6 |
|||
!style="padding: 0em .5em;"|6 |
|||
!7 |
|||
!style="padding: 0em .5em;"|7 |
|||
!8 |
|||
!style="padding: 0em .5em;"|8 |
|||
!9 |
|||
!style="padding: 0em .5em;"|9 |
|||
!10 |
|||
!style="padding: 0em .5em;"|10 |
|||
!11 |
|||
!style="padding: 0em .5em;"|11 |
|||
!12 |
|||
!style="padding: 0em .5em;"|12 |
|||
!13 |
|||
!style="padding: 0em .5em;"|13 |
|||
!14 |
|||
!style="padding: 0em .5em;"|14 |
|||
!.. |
|||
!style="padding: 0em .5em;"|.. |
|||
!style="padding: 0em .5em;"|24 |
|||
!style="padding: 0em .5em;"|25 |
|||
!style="padding: 0em .5em;"|26 |
|||
|- |
|- |
||
!U |
!U |
||
|1 |
|1 |
||
|0 |
|0 |
||
| 第284行: | 第248行: | ||
|45,752 |
|45,752 |
||
|.. |
|.. |
||
|28,439,272,956,934 |
|||
|275,986,683,743,434 |
|||
|2,789,712,466,510,289 |
|||
|- |
|- |
||
!D |
!D |
||
|1 |
|1 |
||
|0 |
|0 |
||
| 第304行: | 第265行: | ||
|365,596 |
|365,596 |
||
|.. |
|.. |
||
|227,514,171,973,736 |
|||
|2,207,893,435,808,352 |
|||
|22,317,699,616,364,044 |
|||
|} |
|} |
||
可以注意到六皇后问题的解的个数比五皇后问题的解的个数要少。现在还没有已知公式可以对 |
可以注意到六皇后问题的解的个数比五皇后问题的解的个数要少。现在还没有已知公式可以对''n''计算''n''皇后问题的解的个数。 |
||
== |
== 示例程序 == |
||
下面是求解n皇后的[[C语言|C]]代码,在程序中可以自己设置n个皇后以及选择是否打印出具体解。 |
|||
{{reflistH|1}} |
|||
<syntaxhighlight lang="C"> |
|||
* Watkins, John J. (2004). ''Across the Board: The Mathematics of Chess Problems''. Princeton: Princeton University Press. ISBN 0-691-11503-6. |
|||
#include <stdio.h> |
|||
* [[Ole-Johan Dahl|O.-J. Dahl]], [[E. W. Dijkstra]], [[C. A. R. Hoare]] ''Structured Programming'', Academic Press, London, 1972 ISBN 0-12-200550-3 see pp 72-82 for Dijkstra's solution of the 8 Queens problem. |
|||
{{reflistF}} |
|||
#define QUEENS 8 /*皇后数量*/ |
|||
#define IS_OUTPUT 1 /*(IS_OUTPUT=0 or 1),Output用于选择是否输出具体解,为1输出,为0不输出*/ |
|||
int A[QUEENS + 1], B[QUEENS * 3 + 1], C[QUEENS * 3 + 1], k[QUEENS + 1][QUEENS + 1]; |
|||
int inc, *a = A, *b = B + QUEENS, *c = C; |
|||
void lay(int i) { |
|||
int j = 0, t, u; |
|||
while (++j <= QUEENS) |
|||
if (a[j] + b[j - i] + c[j + i] == 0) { |
|||
k[i][j] = a[j] = b[j - i] = c[j + i] = 1; |
|||
if (i < QUEENS) lay(i + 1); |
|||
else { |
|||
++inc; |
|||
if (IS_OUTPUT) { |
|||
for (printf("(%d)\n", inc), u = QUEENS + 1; --u; printf("\n")) |
|||
for (t = QUEENS + 1; --t; ) k[t][u] ? printf("Q ") : printf("+ "); |
|||
printf("\n\n\n"); |
|||
} |
|||
} |
|||
a[j] = b[j - i] = c[j + i] = k[i][j] = 0; |
|||
} |
|||
} |
|||
int main(void) { |
|||
lay(1); |
|||
printf("%d皇后共计%d个解\n", QUEENS, inc); |
|||
return 0; |
|||
}</syntaxhighlight> |
|||
以下列出[[尼克劳斯·维尔特]]的[[Pascal (编程语言)|Pascal语言]]程序<ref>Wirth, 1976, p. 145</ref>。此程序找出了八皇后问题的一个解。 |
|||
<syntaxhighlight lang="pascal">program eightqueen1(output); |
|||
var i : integer; q : boolean; |
|||
a : array[ 1 .. 8] of boolean; |
|||
b : array[ 2 .. 16] of boolean; |
|||
c : array[ -7 .. 7] of boolean; |
|||
x : array[ 1 .. 8] of integer; |
|||
procedure try( i : integer; var q : boolean); |
|||
var j : integer; |
|||
begin |
|||
j := 0; |
|||
repeat |
|||
j := j + 1; |
|||
q := false; |
|||
if a[ j] and b[ i + j] and c[ i - j] then |
|||
begin |
|||
x[ i ] := j; |
|||
a[ j ] := false; |
|||
b[ i + j] := false; |
|||
c[ i - j] := false; |
|||
if i < 8 then |
|||
begin |
|||
try( i + 1, q); |
|||
if not q then |
|||
begin |
|||
a[ j] := true; |
|||
b[ i + j] := true; |
|||
c[ i - j] := true; |
|||
end |
|||
end |
|||
else |
|||
q := true |
|||
end |
|||
until q or (j = 8); |
|||
end; |
|||
begin |
|||
for i := 1 to 8 do a[ i] := true; |
|||
for i := 2 to 16 do b[ i] := true; |
|||
for i := -7 to 7 do c[ i] := true; |
|||
try( 1, q); |
|||
if q then |
|||
for i := 1 to 8 do write( x[ i]:4); |
|||
writeln |
|||
end.</syntaxhighlight> |
|||
使用回溯法进行求解八皇后问题 |
|||
<syntaxhighlight lang="C"> |
|||
#include<stdio.h> |
|||
#define PRINTF_IN 1 //定义是否打印,1:打印,0:不打印 |
|||
int queens(int Queens){ |
|||
int i, k, flag, not_finish=1, count=0; |
|||
//正在处理的元素下标,表示前i-1个元素已符合要求,正在处理第i个元素 |
|||
int a[Queens+1]; //八皇后问题的皇后所在的行列位置,从1幵始算起,所以加1 |
|||
i=1; |
|||
a[1]=1; //为数组的第一个元素赋初值 |
|||
printf("%d皇后的可能配置是:",Queens); |
|||
while(not_finish){ //not_finish=l:处理尚未结束 |
|||
while(not_finish && i<=Queens){ //处理尚未结束且还没处理到第Queens个元素 |
|||
for(flag=1,k=1; flag && k<i; k++) //判断是否有多个皇后在同一行 |
|||
if(a[k]==a[i]) |
|||
flag=0; |
|||
for (k=1; flag&&k<i; k++) //判断是否有多个皇后在同一对角线 |
|||
if( (a[i]==a[k]-(k-i)) || (a[i]==a[k]+(k-i)) ) |
|||
flag=0; |
|||
if(!flag){ //若存在矛盾不满足要求,需要重新设置第i个元素 |
|||
if(a[i]==a[i-1]){ //若a[i]的值已经经过一圈追上a[i-1]的值 |
|||
i--; //退回一步,重新试探处理前一个元素 |
|||
if(i>1 && a[i]==Queens) |
|||
a[i]=1; //当a[i]为Queens时将a[i]的值置1 |
|||
else |
|||
if(i==1 && a[i]==Queens) |
|||
not_finish=0; //当第一位的值达到Queens时结束 |
|||
else |
|||
a[i]++; //将a[il的值取下一个值 |
|||
}else if(a[i] == Queens) |
|||
a[i]=1; |
|||
else |
|||
a[i]++; //将a[i]的值取下一个值 |
|||
}else if(++i<=Queens) |
|||
if(a[i-1] == Queens ) |
|||
a[i]=1; //若前一个元素的值为Queens则a[i]=l |
|||
else |
|||
a[i] = a[i-1]+1; //否则元素的值为前一个元素的下一个值 |
|||
} |
|||
if(not_finish){ |
|||
++count; |
|||
if(PRINTF_IN){ |
|||
printf((count-1)%3 ? " [%2d]:" : "\n[%2d]:", count); |
|||
for(k=1; k<=Queens; k++) //输出结果 |
|||
printf(" %d", a[k]); |
|||
} |
|||
if(a[Queens-1]<Queens ) |
|||
a[Queens-1]++; //修改倒数第二位的值 |
|||
else |
|||
a[Queens-1]=1; |
|||
i=Queens -1; //开始寻找下一个满足条件的解 |
|||
} |
|||
} |
|||
return count; |
|||
} |
|||
int main() |
|||
{ |
|||
int Num ; |
|||
printf("输入一个N皇后数值:"); |
|||
scanf("%d" , &Num); |
|||
printf("\n%d皇后有%d种配置\n",Num,queens(Num)); |
|||
}</syntaxhighlight> |
|||
使用回溯法进行求解八皇后问题(Java版本),可直接复制到 [https://leetcode.com/problems/n-queens/ N-Queens - LeetCode] {{Wayback|url=https://leetcode.com/problems/n-queens/ |date=20210517181757 }} 测试。 |
|||
<syntaxhighlight lang="Java"> |
|||
class Solution { |
|||
public List<List<String>> solveNQueens(int n) { |
|||
List<List<String>> results = new ArrayList<>(); |
|||
// 使用 char[][] 是为了展示结果时,直接使用 new String(char[])。 |
|||
// 一般情况下,使用 boolean[][] 即可。 |
|||
char[][] result = new char[n][n]; |
|||
for (int i = 0; i < n; ++i) { |
|||
for (int j = 0; j < n; ++j) { |
|||
result[i][j] = '.'; |
|||
} |
|||
} |
|||
backtrack(results, result, 0); |
|||
return results; |
|||
} |
|||
private static void backtrack(List<List<String>> results, char[][] result, int x) { |
|||
for (int j = 0; j < result.length; ++j) { |
|||
if (isValid(result, x, j)) { |
|||
result[x][j] = 'Q'; |
|||
if (x == result.length - 1) { |
|||
showResult(results, result); |
|||
// 可以直接 break |
|||
} else { |
|||
// 皇后问题中,不会出现一行出现多个,所以直接跳到下一行 |
|||
backtrack(results, result, x + 1); |
|||
} |
|||
result[x][j] = '.'; |
|||
} |
|||
} |
|||
} |
|||
private static boolean isValid(char[][] result, int x, int y) { |
|||
// ... (0, y) |
|||
// ... ...... |
|||
// ... (x-1, y) |
|||
// ... (x, y) |
|||
for (int i = 0; i < x; ++i) { |
|||
if (result[i][y] == 'Q') { |
|||
return false; |
|||
} |
|||
} |
|||
// ... |
|||
// ... (x-1, y-1) |
|||
// ... .......... (x, y) |
|||
for (int i = x - 1, j = y - 1; i >= 0 && j >= 0; --i, --j) { |
|||
if (result[i][j] == 'Q') { |
|||
return false; |
|||
} |
|||
} |
|||
// ... |
|||
// ... ...... (x-1, y+1) |
|||
// ... (x, y) |
|||
for (int i = x - 1, j = y + 1; i >= 0 && j < result.length; --i, ++j) { |
|||
if (result[i][j] == 'Q') { |
|||
return false; |
|||
} |
|||
} |
|||
return true; |
|||
} |
|||
private static void showResult(List<List<String>> results, char[][] result) { |
|||
List<String> list = new ArrayList<>(result.length); |
|||
for (char[] value : result) { |
|||
list.add(new String(value)); |
|||
} |
|||
results.add(list); |
|||
} |
|||
} |
|||
</syntaxhighlight> |
|||
<syntaxhighlight lang="C"> |
|||
#include "iostream" |
|||
#include "cmath" |
|||
using namespace std; |
|||
#define Max 20 //定義棋盤的最大值 |
|||
int a[Max]; |
|||
int show(int S) //定義出函數 |
|||
{ |
|||
int i,p,q; |
|||
int b[Max][Max]={0}; //定義且初始化b[1][]輸出模組 |
|||
for(i=1;i<=S;i++) //按橫列順序輸出a[i]的座標 |
|||
{ |
|||
b[i][a[i]]=1; |
|||
printf("(%d,%d)\t",i,a[i]); |
|||
} |
|||
printf("\n"); |
|||
for(p=1;p<=S;p++) //按棋盤的橫列的順序標明的位置 |
|||
{ |
|||
for(q=1;q<=S;q++) |
|||
{ |
|||
if(b[p][q]==1) //在第p行第q列放置一顆棋子 |
|||
printf("x"); |
|||
else |
|||
printf("o"); |
|||
} |
|||
printf("\n"); |
|||
} |
|||
return 0; |
|||
} |
|||
int check(int k) //定義check函數 |
|||
{ |
|||
int i; |
|||
for(i=1;i<k;i++) |
|||
{ |
|||
if((a[i]==a[k]) || (a[i]-a[k]==k-i)|| (a[i]-a[k]==i-k) ) //檢查是否有多顆棋子在同一個直行上 |
|||
{ |
|||
return 0; |
|||
} |
|||
} |
|||
return 1; |
|||
} |
|||
void check_m(int num) //定義函數 |
|||
{ |
|||
int k=1,count=0; |
|||
printf("N皇后問題的所有解(包含經由旋轉的解):\n"); |
|||
a[k]=1; |
|||
while(k>0) |
|||
{ |
|||
if(k<=num && a[k]<=num) //從第k行第一列的位置開始,尋找之後的棋子的位置 |
|||
{ |
|||
if(check(k)==0) //第k行的a[k]列不能放置棋子 |
|||
{ |
|||
a[k]++; //繼續試探該前行的下一列:a[k+1] |
|||
} |
|||
else |
|||
{ |
|||
k++; //第K行的位置已經確定完畢,繼續尋找第k+1行棋子的位置 |
|||
a[k]=1; //從第k+1的第一列開始查找 |
|||
} |
|||
} |
|||
else |
|||
{ |
|||
if(k>num) //若滿足輸出數組的要求就輸出該數組 |
|||
{ |
|||
count++; |
|||
printf("[%d]: ",count); |
|||
show(num); //調用輸出函數show() |
|||
} |
|||
k--; //棋子位置不符合要求則退回前一步 |
|||
a[k]++; //繼續尋找下一列位置 |
|||
} |
|||
} |
|||
printf("總共有 %d \n",count,"個"); |
|||
} |
|||
int main(void) |
|||
{ |
|||
int N,d; |
|||
do |
|||
{ |
|||
printf(" N皇后問題的解(N<20) \n"); |
|||
printf("請輸入N的值:_"); |
|||
scanf("%d",&N); |
|||
printf("\n"); |
|||
if(N>0&&N<20) |
|||
{ |
|||
check_m(N); |
|||
break; |
|||
} |
|||
else |
|||
{ |
|||
printf("輸入錯誤,請重新輸入"); |
|||
printf("\n\n"); |
|||
break; |
|||
} |
|||
} |
|||
while(1); |
|||
system("pause"); |
|||
return 0; |
|||
} |
|||
</syntaxhighlight> |
|||
==大众文化== |
|||
*電腦游戲《[[第七訪客]]》中,伊格(Ego,玩家)在史陶夫的[[宅第|府邸]]的游戲室裏碰到的象棋問題正是八個皇后問題。<ref name=Guide_Book>{{cite book|url=http://www.thealmightyguru.com/Wiki/images/a/a7/7th_Guest%2C_The_-_Official_Strategy_Guide%2C_The.pdf|title=The 7th Guest: The Official Strategy Guide|first=Rusel|last=DeMaria|publisher=Prima Games|ISBN=978-1559584685|date=1993-11-15|access-date=2021-04-22|archive-date=2021-04-22|archive-url=https://web.archive.org/web/20210422014404/http://www.thealmightyguru.com/Wiki/images/a/a7/7th_Guest,_The_-_Official_Strategy_Guide,_The.pdf|dead-url=no}}</ref>{{rp|pages=48-49,289-290}} |
|||
==延伸阅读== |
|||
* {{cite journal|last1=Bell |first1=Jordan |last2=Stevens |first2=Brett |
|||
|title=A survey of known results and research areas for '''n'''-queens |
|||
|journal=Discrete Mathematics|volume=309 |number=1|year=2009|pages=1–31|doi=10.1016/j.disc.2007.12.043}} |
|||
* {{cite book|last1=Watkins|first1=John J.|year=2004|title=Across the Board: The Mathematics of Chess Problems|location=Princeton|publisher=Princeton University Press|isbn=978-0-691-11503-0|url-access=registration|url=https://archive.org/details/acrossboardma00watk}} |
|||
* [[Ole-Johan Dahl|O.-J. Dahl]], [[E. W. Dijkstra]], [[C. A. R. Hoare]] ''Structured Programming'', Academic Press, London, 1972 {{ISBN|0-12-200550-3}} see pp. 72–82 for Dijkstra's solution of the 8 Queens problem. |
|||
* {{cite web|url=http://www.csse.monash.edu.au/~lloyd/tildeAlgDS/Recn/Queens3D/|title=Three Dimensional NxN-Queens Problems|first1=L.|last1=Allison|first2=C.N.|last2=Yee|first3=M.|last3=McGaughey|year=1988|location=Department of Computer Science, Monash University, Australia|access-date=2021-03-23|archive-date=2009-07-01|archive-url=https://web.archive.org/web/20090701015319/http://www.csse.monash.edu.au/~lloyd/tildeAlgDS/Recn/Queens3D/|dead-url=no}} |
|||
* {{cite journal|first1=S. |last1= Nudelman |title=The Modular N-Queens Problem in Higher Dimensions |
|||
|journal=Discrete Mathematics|volume=146 |number=1–3|year=1995|pages=159–167|doi=10.1016/0012-365X(94)00161-5}} |
|||
* {{cite journal |first1=M. |last1=Engelhardt |title=Der Stammbaum der Lösungen des Damenproblems (in German, means The pedigree chart of solutions to the 8-queens problem |journal=Spektrum der Wissenschaft |date=August 2010 |pages=68–71 |url=http://www.spektrum.de/artikel/1037434&_z=798888 |access-date=2022-02-19 |archive-date=2013-01-28 |archive-url=https://web.archive.org/web/20130128173314/http://www.spektrum.de/artikel/1037434%26_z%3D798888 |dead-url=no }} |
|||
* [http://www.liacs.nl/~kosters/nqueens/papers/gomez2004.pdf ''On The Modular N-Queen Problem in Higher Dimensions''] {{Wayback|url=http://www.liacs.nl/~kosters/nqueens/papers/gomez2004.pdf |date=20140616193131 }}, Ricardo Gomez, Juan Jose Montellano and Ricardo Strausz (2004), Instituto de Matematicas, Area de la Investigacion Cientifica, Circuito Exterior, Ciudad Universitaria, Mexico. |
|||
* {{citation |
|||
|last= Wirth |first=Niklaus| author-link=Niklaus Wirth |
|||
| title=Algorithms + Data Structures = Programs |
|||
|journal=Prentice-Hall Series in Automatic Computation|publisher=Prentice-Hall |
|||
| year=1976 |
|||
| isbn=978-0-13-022418-7|title-link=Algorithms + Data Structures = Programs|bibcode=1976adsp.book.....W}} |
|||
* {{cite book|last=Wirth|first=Niklaus|date=2004|orig-year=updated 2012|title=Algorithms and Data Structures|version=Oberon version with corrections and authorized modifications|url=https://people.inf.ethz.ch/wirth/AD.pdf|chapter=The Eight Queens Problem|pages=114-118|access-date=2021-03-23|archive-date=2021-04-17|archive-url=https://web.archive.org/web/20210417040502/https://people.inf.ethz.ch/wirth/AD.pdf|dead-url=no}} |
|||
== 參考資料 == |
|||
{{reflist}} |
|||
{{Authority control}} |
|||
[[Category:国际象棋]] |
|||
[[Category: |
[[Category:數學西洋棋問題]] |
||
[[Category: |
[[Category:组合数学]] |
||
[[Category:组合]] |
[[Category:组合计数]] |
||
[[Category:数学问题]] |
|||
[[Category:下棋问题]] |
|||
[[ca:Vuit reines]] |
|||
[[cs:Problém osmi dam]] |
|||
[[da:8-dronningeproblemet]] |
|||
[[de:Damenproblem]] |
|||
[[en:Eight queens puzzle]] |
|||
[[es:Problema de las ocho reinas]] |
|||
[[fr:Problème des huit dames]] |
|||
[[he:חידת שמונה המלכות]] |
|||
[[hu:Nyolckirálynő-probléma]] |
|||
[[it:Rompicapo delle otto regine]] |
|||
[[ja:エイト・クイーン]] |
|||
[[ka:რვა ლაზიერის ამოცანა]] |
|||
[[pl:Problem ośmiu hetmanów]] |
|||
[[pt:Problema das oito damas]] |
|||
[[sl:Problem osmih dam]] |
|||
[[sr:Проблем осам дама]] |
|||
[[th:ปริศนาควีนแปดตัว]] |
|||
[[tr:Sekiz vezir bulmacası]] |
|||
[[vi:Bài toán tám quân hậu]] |
|||
2024年2月16日 (五) 14:15的最新版本
| a | b | c | d | e | f | g | h | ||
| 8 |  | 8 | |||||||
| 7 | 7 | ||||||||
| 6 | 6 | ||||||||
| 5 | 5 | ||||||||
| 4 | 4 | ||||||||
| 3 | 3 | ||||||||
| 2 | 2 | ||||||||
| 1 | 1 | ||||||||
| a | b | c | d | e | f | g | h | ||
八皇后问题是一个以国际象棋为背景的问题:如何能够在8×8的国际象棋棋盘上放置八个皇后,使得任何一个皇后都无法直接吃掉其他的皇后?为了达到此目的,任两个皇后都不能处于同一条横行、纵行或斜线上。八皇后问题可以推广为更一般的n皇后摆放问题:这时棋盘的大小变为n×n,而皇后个数也变成n。当且仅当n = 1或n ≥ 4时问题有解[1]。
历史
[编辑]八皇后问题最早是由西洋棋棋手马克斯·贝瑟尔(Max Bezzel)于1848年提出。第一个解在1850年由弗朗兹·诺克(Franz Nauck)给出。并且将其推广为更一般的n皇后摆放问题。诺克也是首先将问题推广到更一般的n皇后摆放问题的人之一。
在此之后,陆续有数学家对其进行研究,其中包括高斯和康托,1874年,S.冈德尔提出了一个通过行列式来求解的方法[2],这个方法后来又被J.W.L.格莱舍加以改进。
1972年,艾兹格·迪杰斯特拉用这个问题为例来说明他所谓结构化编程的能力[3]。他对深度优先搜索回溯算法有着非常详尽的描述2。
八皇后问题在1990年代初期的著名电子游戏《第七访客》和NDS平台的著名电子游戏《雷顿教授与不可思议的小镇》中都有出现。
解题方法
[编辑]八个皇后在8x8棋盘上共有4,426,165,368(64C8)种摆放方法,但只有92个可行(皇后間互不攻擊)的解。如果将旋转和对称的解归为一种的话,则一共有12个独立解,具体如下:
独立解1
|
独立解2
|
独立解3
|
独立解4
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
独立解5
|
独立解6
|
独立解7
|
独立解8
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
独立解9
|
独立解10
|
独立解11
|
独立解12
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
解的个数
[编辑]下表给出了n皇后问题的解的个数包括独立解U(OEIS數列A002562)以及可行解D(OEIS數列A000170)的个数:
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | .. |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| U | 1 | 0 | 0 | 1 | 2 | 1 | 6 | 12 | 46 | 92 | 341 | 1,787 | 9,233 | 45,752 | .. |
| D | 1 | 0 | 0 | 2 | 10 | 4 | 40 | 92 | 352 | 724 | 2,680 | 14,200 | 73,712 | 365,596 | .. |
可以注意到六皇后问题的解的个数比五皇后问题的解的个数要少。现在还没有已知公式可以对n计算n皇后问题的解的个数。
示例程序
[编辑]下面是求解n皇后的C代码,在程序中可以自己设置n个皇后以及选择是否打印出具体解。
#include <stdio.h>
#define QUEENS 8 /*皇后数量*/
#define IS_OUTPUT 1 /*(IS_OUTPUT=0 or 1),Output用于选择是否输出具体解,为1输出,为0不输出*/
int A[QUEENS + 1], B[QUEENS * 3 + 1], C[QUEENS * 3 + 1], k[QUEENS + 1][QUEENS + 1];
int inc, *a = A, *b = B + QUEENS, *c = C;
void lay(int i) {
int j = 0, t, u;
while (++j <= QUEENS)
if (a[j] + b[j - i] + c[j + i] == 0) {
k[i][j] = a[j] = b[j - i] = c[j + i] = 1;
if (i < QUEENS) lay(i + 1);
else {
++inc;
if (IS_OUTPUT) {
for (printf("(%d)\n", inc), u = QUEENS + 1; --u; printf("\n"))
for (t = QUEENS + 1; --t; ) k[t][u] ? printf("Q ") : printf("+ ");
printf("\n\n\n");
}
}
a[j] = b[j - i] = c[j + i] = k[i][j] = 0;
}
}
int main(void) {
lay(1);
printf("%d皇后共计%d个解\n", QUEENS, inc);
return 0;
}
以下列出尼克劳斯·维尔特的Pascal语言程序[4]。此程序找出了八皇后问题的一个解。
program eightqueen1(output);
var i : integer; q : boolean;
a : array[ 1 .. 8] of boolean;
b : array[ 2 .. 16] of boolean;
c : array[ -7 .. 7] of boolean;
x : array[ 1 .. 8] of integer;
procedure try( i : integer; var q : boolean);
var j : integer;
begin
j := 0;
repeat
j := j + 1;
q := false;
if a[ j] and b[ i + j] and c[ i - j] then
begin
x[ i ] := j;
a[ j ] := false;
b[ i + j] := false;
c[ i - j] := false;
if i < 8 then
begin
try( i + 1, q);
if not q then
begin
a[ j] := true;
b[ i + j] := true;
c[ i - j] := true;
end
end
else
q := true
end
until q or (j = 8);
end;
begin
for i := 1 to 8 do a[ i] := true;
for i := 2 to 16 do b[ i] := true;
for i := -7 to 7 do c[ i] := true;
try( 1, q);
if q then
for i := 1 to 8 do write( x[ i]:4);
writeln
end.
使用回溯法进行求解八皇后问题
#include<stdio.h>
#define PRINTF_IN 1 //定义是否打印,1:打印,0:不打印
int queens(int Queens){
int i, k, flag, not_finish=1, count=0;
//正在处理的元素下标,表示前i-1个元素已符合要求,正在处理第i个元素
int a[Queens+1]; //八皇后问题的皇后所在的行列位置,从1幵始算起,所以加1
i=1;
a[1]=1; //为数组的第一个元素赋初值
printf("%d皇后的可能配置是:",Queens);
while(not_finish){ //not_finish=l:处理尚未结束
while(not_finish && i<=Queens){ //处理尚未结束且还没处理到第Queens个元素
for(flag=1,k=1; flag && k<i; k++) //判断是否有多个皇后在同一行
if(a[k]==a[i])
flag=0;
for (k=1; flag&&k<i; k++) //判断是否有多个皇后在同一对角线
if( (a[i]==a[k]-(k-i)) || (a[i]==a[k]+(k-i)) )
flag=0;
if(!flag){ //若存在矛盾不满足要求,需要重新设置第i个元素
if(a[i]==a[i-1]){ //若a[i]的值已经经过一圈追上a[i-1]的值
i--; //退回一步,重新试探处理前一个元素
if(i>1 && a[i]==Queens)
a[i]=1; //当a[i]为Queens时将a[i]的值置1
else
if(i==1 && a[i]==Queens)
not_finish=0; //当第一位的值达到Queens时结束
else
a[i]++; //将a[il的值取下一个值
}else if(a[i] == Queens)
a[i]=1;
else
a[i]++; //将a[i]的值取下一个值
}else if(++i<=Queens)
if(a[i-1] == Queens )
a[i]=1; //若前一个元素的值为Queens则a[i]=l
else
a[i] = a[i-1]+1; //否则元素的值为前一个元素的下一个值
}
if(not_finish){
++count;
if(PRINTF_IN){
printf((count-1)%3 ? " [%2d]:" : "\n[%2d]:", count);
for(k=1; k<=Queens; k++) //输出结果
printf(" %d", a[k]);
}
if(a[Queens-1]<Queens )
a[Queens-1]++; //修改倒数第二位的值
else
a[Queens-1]=1;
i=Queens -1; //开始寻找下一个满足条件的解
}
}
return count;
}
int main()
{
int Num ;
printf("输入一个N皇后数值:");
scanf("%d" , &Num);
printf("\n%d皇后有%d种配置\n",Num,queens(Num));
}
使用回溯法进行求解八皇后问题(Java版本),可直接复制到 N-Queens - LeetCode (页面存档备份,存于互联网档案馆) 测试。
class Solution {
public List<List<String>> solveNQueens(int n) {
List<List<String>> results = new ArrayList<>();
// 使用 char[][] 是为了展示结果时,直接使用 new String(char[])。
// 一般情况下,使用 boolean[][] 即可。
char[][] result = new char[n][n];
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
result[i][j] = '.';
}
}
backtrack(results, result, 0);
return results;
}
private static void backtrack(List<List<String>> results, char[][] result, int x) {
for (int j = 0; j < result.length; ++j) {
if (isValid(result, x, j)) {
result[x][j] = 'Q';
if (x == result.length - 1) {
showResult(results, result);
// 可以直接 break
} else {
// 皇后问题中,不会出现一行出现多个,所以直接跳到下一行
backtrack(results, result, x + 1);
}
result[x][j] = '.';
}
}
}
private static boolean isValid(char[][] result, int x, int y) {
// ... (0, y)
// ... ......
// ... (x-1, y)
// ... (x, y)
for (int i = 0; i < x; ++i) {
if (result[i][y] == 'Q') {
return false;
}
}
// ...
// ... (x-1, y-1)
// ... .......... (x, y)
for (int i = x - 1, j = y - 1; i >= 0 && j >= 0; --i, --j) {
if (result[i][j] == 'Q') {
return false;
}
}
// ...
// ... ...... (x-1, y+1)
// ... (x, y)
for (int i = x - 1, j = y + 1; i >= 0 && j < result.length; --i, ++j) {
if (result[i][j] == 'Q') {
return false;
}
}
return true;
}
private static void showResult(List<List<String>> results, char[][] result) {
List<String> list = new ArrayList<>(result.length);
for (char[] value : result) {
list.add(new String(value));
}
results.add(list);
}
}
#include "iostream"
#include "cmath"
using namespace std;
#define Max 20 //定義棋盤的最大值
int a[Max];
int show(int S) //定義出函數
{
int i,p,q;
int b[Max][Max]={0}; //定義且初始化b[1][]輸出模組
for(i=1;i<=S;i++) //按橫列順序輸出a[i]的座標
{
b[i][a[i]]=1;
printf("(%d,%d)\t",i,a[i]);
}
printf("\n");
for(p=1;p<=S;p++) //按棋盤的橫列的順序標明的位置
{
for(q=1;q<=S;q++)
{
if(b[p][q]==1) //在第p行第q列放置一顆棋子
printf("x");
else
printf("o");
}
printf("\n");
}
return 0;
}
int check(int k) //定義check函數
{
int i;
for(i=1;i<k;i++)
{
if((a[i]==a[k]) || (a[i]-a[k]==k-i)|| (a[i]-a[k]==i-k) ) //檢查是否有多顆棋子在同一個直行上
{
return 0;
}
}
return 1;
}
void check_m(int num) //定義函數
{
int k=1,count=0;
printf("N皇后問題的所有解(包含經由旋轉的解):\n");
a[k]=1;
while(k>0)
{
if(k<=num && a[k]<=num) //從第k行第一列的位置開始,尋找之後的棋子的位置
{
if(check(k)==0) //第k行的a[k]列不能放置棋子
{
a[k]++; //繼續試探該前行的下一列:a[k+1]
}
else
{
k++; //第K行的位置已經確定完畢,繼續尋找第k+1行棋子的位置
a[k]=1; //從第k+1的第一列開始查找
}
}
else
{
if(k>num) //若滿足輸出數組的要求就輸出該數組
{
count++;
printf("[%d]: ",count);
show(num); //調用輸出函數show()
}
k--; //棋子位置不符合要求則退回前一步
a[k]++; //繼續尋找下一列位置
}
}
printf("總共有 %d \n",count,"個");
}
int main(void)
{
int N,d;
do
{
printf(" N皇后問題的解(N<20) \n");
printf("請輸入N的值:_");
scanf("%d",&N);
printf("\n");
if(N>0&&N<20)
{
check_m(N);
break;
}
else
{
printf("輸入錯誤,請重新輸入");
printf("\n\n");
break;
}
}
while(1);
system("pause");
return 0;
}
大众文化
[编辑]延伸阅读
[编辑]- Bell, Jordan; Stevens, Brett. A survey of known results and research areas for n-queens. Discrete Mathematics. 2009, 309 (1): 1–31. doi:10.1016/j.disc.2007.12.043.
- Watkins, John J. Across the Board: The Mathematics of Chess Problems
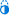 . Princeton: Princeton University Press. 2004. ISBN 978-0-691-11503-0.
. Princeton: Princeton University Press. 2004. ISBN 978-0-691-11503-0. - O.-J. Dahl, E. W. Dijkstra, C. A. R. Hoare Structured Programming, Academic Press, London, 1972 ISBN 0-12-200550-3 see pp. 72–82 for Dijkstra's solution of the 8 Queens problem.
- Allison, L.; Yee, C.N.; McGaughey, M. Three Dimensional NxN-Queens Problems. Department of Computer Science, Monash University, Australia. 1988 [2021-03-23]. (原始内容存档于2009-07-01).
- Nudelman, S. The Modular N-Queens Problem in Higher Dimensions. Discrete Mathematics. 1995, 146 (1–3): 159–167. doi:10.1016/0012-365X(94)00161-5.
- Engelhardt, M. Der Stammbaum der Lösungen des Damenproblems (in German, means The pedigree chart of solutions to the 8-queens problem. Spektrum der Wissenschaft. August 2010: 68–71 [2022-02-19]. (原始内容存档于2013-01-28).
- On The Modular N-Queen Problem in Higher Dimensions (页面存档备份,存于互联网档案馆), Ricardo Gomez, Juan Jose Montellano and Ricardo Strausz (2004), Instituto de Matematicas, Area de la Investigacion Cientifica, Circuito Exterior, Ciudad Universitaria, Mexico.
- Wirth, Niklaus, Algorithms + Data Structures = Programs, Prentice-Hall Series in Automatic Computation (Prentice-Hall), 1976, Bibcode:1976adsp.book.....W, ISBN 978-0-13-022418-7
- Wirth, Niklaus. The Eight Queens Problem. Algorithms and Data Structures (PDF). Oberon version with corrections and authorized modifications. 2004: 114–118 [updated 2012] [2021-03-23]. (原始内容存档 (PDF)于2021-04-17).
參考資料
[编辑]- ^ Watkins, John J. (2004). Across the Board: The Mathematics of Chess Problems. Princeton: Princeton University Press. ISBN 0-691-11503-6
- ^ W. W. Rouse Ball (1960) The Eight Queens Problem, in Mathematical Recreations and Essays, Macmillan, New York, pp 165-171.
- ^ 奧利-約翰·達爾, 艾兹赫尔·戴克斯特拉, 東尼·霍爾 Structured Programming, Academic Press, London, 1972 ISBN 0-12-200550-3 see pp 72-82 for Dijkstra's solution of the 8 Queens problem.
- ^ Wirth, 1976, p. 145
- ^ DeMaria, Rusel. The 7th Guest: The Official Strategy Guide (PDF). Prima Games. 1993-11-15 [2021-04-22]. ISBN 978-1559584685. (原始内容存档 (PDF)于2021-04-22).

