
In chemistry, solubility is the ability of a substance, the solute, to form a solution with another substance, the solvent. Insolubility is the opposite property, the inability of the solute to form such a solution.
Solubility equilibrium is a type of dynamic equilibrium that exists when a chemical compound in the solid state is in chemical equilibrium with a solution of that compound. The solid may dissolve unchanged, with dissociation, or with chemical reaction with another constituent of the solution, such as acid or alkali. Each solubility equilibrium is characterized by a temperature-dependent solubility product which functions like an equilibrium constant. Solubility equilibria are important in pharmaceutical, environmental and many other scenarios.

A eutectic system or eutectic mixture is a type of a homogeneous mixture that has a melting point lower than those of the constituents. The lowest possible melting point over all of the mixing ratios of the constituents is called the eutectic temperature. On a phase diagram, the eutectic temperature is seen as the eutectic point.

Zone melting is a group of similar methods of purifying crystals, in which a narrow region of a crystal is melted, and this molten zone is moved along the crystal. The molten region melts impure solid at its forward edge and leaves a wake of purer material solidified behind it as it moves through the ingot. The impurities concentrate in the melt, and are moved to one end of the ingot. Zone refining was invented by John Desmond Bernal and further developed by William G. Pfann in Bell Labs as a method to prepare high-purity materials, mainly semiconductors, for manufacturing transistors. Its first commercial use was in germanium, refined to one atom of impurity per ten billion, but the process can be extended to virtually any solute–solvent system having an appreciable concentration difference between solid and liquid phases at equilibrium. This process is also known as the float zone process, particularly in semiconductor materials processing.

Supercooling, also known as undercooling, is the process of lowering the temperature of a liquid below its freezing point without it becoming a solid. As per the established international definition, supercooling means ‘cooling a substance below the normal freezing point without solidification’ While it can be achieved by different physical means, the postponed solidification is most often due to the absence of seed crystals or nuclei around which a crystal structure can form. The supercooling of water can be achieved without any special techniques other than chemical demineralization, down to −48.3 °C (−54.9 °F). Supercooled water can occur naturally, for example in the atmosphere, animals or plants.

In materials science, creep is the tendency of a solid material to undergo slow deformation while subject to persistent mechanical stresses. It can occur as a result of long-term exposure to high levels of stress that are still below the yield strength of the material. Creep is more severe in materials that are subjected to heat for long periods and generally increases as they near their melting point.
In the physical sciences, a partition coefficient (P) or distribution coefficient (D) is the ratio of concentrations of a compound in a mixture of two immiscible solvents at equilibrium. This ratio is therefore a comparison of the solubilities of the solute in these two liquids. The partition coefficient generally refers to the concentration ratio of un-ionized species of compound, whereas the distribution coefficient refers to the concentration ratio of all species of the compound.

In materials science, shear modulus or modulus of rigidity, denoted by G, or sometimes S or μ, is a measure of the elastic shear stiffness of a material and is defined as the ratio of shear stress to the shear strain:
Precipitation hardening, also called age hardening or particle hardening, is a heat treatment technique used to increase the yield strength of malleable materials, including most structural alloys of aluminium, magnesium, nickel, titanium, and some steels, stainless steels, and duplex stainless steel. In superalloys, it is known to cause yield strength anomaly providing excellent high-temperature strength.
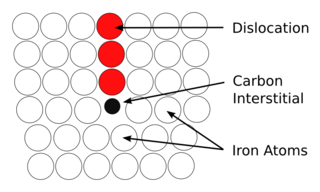
In materials science, the concept of the Cottrell atmosphere was introduced by A. H. Cottrell and B. A. Bilby in 1949 to explain how dislocations are pinned in some metals by boron, carbon, or nitrogen interstitials.
A solid solution, a term popularly used for metals, is a homogeneous mixture of two different kinds of atoms in solid state and having a single crystal structure. Many examples can be found in metallurgy, geology, and solid-state chemistry. The word "solution" is used to describe the intimate mixing of components at the atomic level and distinguishes these homogeneous materials from physical mixtures of components. Two terms are mainly associated with solid solutions – solvents and solutes, depending on the relative abundance of the atomic species.

A dendrite in metallurgy is a characteristic tree-like structure of crystals growing as molten metal solidifies, the shape produced by faster growth along energetically favourable crystallographic directions. This dendritic growth has large consequences in regard to material properties.
In metallurgy, solid solution strengthening is a type of alloying that can be used to improve the strength of a pure metal. The technique works by adding atoms of one element to the crystalline lattice of another element, forming a solid solution. The local nonuniformity in the lattice due to the alloying element makes plastic deformation more difficult by impeding dislocation motion through stress fields. In contrast, alloying beyond the solubility limit can form a second phase, leading to strengthening via other mechanisms.
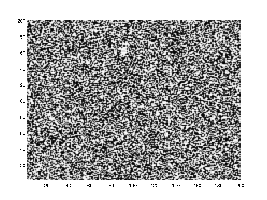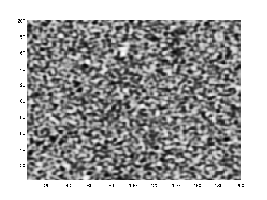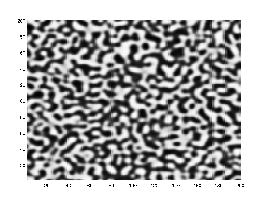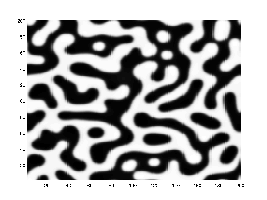
Spinodal decomposition is a mechanism by which a single thermodynamic phase spontaneously separates into two phases. Decomposition occurs when there is no thermodynamic barrier to phase separation. As a result, phase separation via decomposition does not require the nucleation events resulting from thermodynamic fluctuations, which normally trigger phase separation.
In materials science, segregation is the enrichment of atoms, ions, or molecules at a microscopic region in a materials system. While the terms segregation and adsorption are essentially synonymous, in practice, segregation is often used to describe the partitioning of molecular constituents to defects from solid solutions, whereas adsorption is generally used to describe such partitioning from liquids and gases to surfaces. The molecular-level segregation discussed in this article is distinct from other types of materials phenomena that are often called segregation, such as particle segregation in granular materials, and phase separation or precipitation, wherein molecules are segregated in to macroscopic regions of different compositions. Segregation has many practical consequences, ranging from the formation of soap bubbles, to microstructural engineering in materials science, to the stabilization of colloidal suspensions.
A phase-field model is a mathematical model for solving interfacial problems. It has mainly been applied to solidification dynamics, but it has also been applied to other situations such as viscous fingering, fracture mechanics, hydrogen embrittlement, and vesicle dynamics.

The Langmuir adsorption model explains adsorption by assuming an adsorbate behaves as an ideal gas at isothermal conditions. According to the model, adsorption and desorption are reversible processes. This model even explains the effect of pressure; i.e., at these conditions the adsorbate's partial pressure is related to its volume V adsorbed onto a solid adsorbent. The adsorbent, as indicated in the figure, is assumed to be an ideal solid surface composed of a series of distinct sites capable of binding the adsorbate. The adsorbate binding is treated as a chemical reaction between the adsorbate gaseous molecule and an empty sorption site S. This reaction yields an adsorbed species with an associated equilibrium constant :
Dislocation creep is a deformation mechanism in crystalline materials. Dislocation creep involves the movement of dislocations through the crystal lattice of the material, in contrast to diffusion creep, in which diffusion is the dominant creep mechanism. It causes plastic deformation of the individual crystals, and thus the material itself.

In thermodynamics, the enthalpy of fusion of a substance, also known as (latent) heat of fusion, is the change in its enthalpy resulting from providing energy, typically heat, to a specific quantity of the substance to change its state from a solid to a liquid, at constant pressure.
Miedema's model is a semi-empirical approach for estimating the heat of formation of solid or liquid metal alloys and compounds in the framework of thermodynamic calculations for metals and minerals. It was developed by the Dutch scientist Andries Rinse Miedema while working at Philips Natuurkundig Laboratorium. It may provide or confirm basic enthalpy data needed for the calculation of phase diagrams of metals, via CALPHAD or ab initio quantum chemistry methods. For a binary system composed by elements A and B, a generic Miedema Formula could be cast as where terms Phi and nwS are explained and reported below. For a binary system the physical picture could be simplified by considering a relatively simpler function of the difference of these three physical parameters resulting in a more complex form































