Default logic

Last updated February 29, 2024

Default logic is a non-monotonic logic proposed by Raymond Reiter to formalize reasoning with default assumptions.

Default logic can express facts like “by default, something is true”; by contrast, standard logic can only express that something is true or that something is false. This is a problem because reasoning often involves facts that are true in the majority of cases but not always. A classical example is: “birds typically fly”. This rule can be expressed in standard logic either by “all birds fly”, which is inconsistent with the fact that penguins do not fly, or by “all birds that are not penguins and not ostriches and ... fly”, which requires all exceptions to the rule to be specified. Default logic aims at formalizing inference rules like this one without explicitly mentioning all their exceptions.

Syntax of default logic

A default theory is a pair $\langle W,D\rangle$ . $W$ is a set of logical formulas, called the background theory, that formalize the facts that are known for sure. $D$ is a set of default rules, each one being of the form:

{\frac {\mathrm {Prerequisite:Justification} _{1},\dots ,\mathrm {Justification} _{n}}{\mathrm {Conclusion} }}

According to this default, if we believe that $Prerequisite$ is true, and each $\mathrm {Justification} _{i}$ for $i=1,\dots ,n$ is consistent with our current beliefs, we are led to believe that $Conclusion$ is true.

The logical formulae in $W$ and all formulae in a default were originally assumed to be first-order logic formulae, but they can potentially be formulae in an arbitrary formal logic. The case in which they are formulae in propositional logic is one of the most studied.

Examples

The default rule “birds typically fly” is formalized by the following default:

D=\left\{{\frac {\mathrm {Bird} (X):\mathrm {Flies} (X)}{\mathrm {Flies} (X)}}\right\}

This rule means that, "if $X$ is a bird, and it can be assumed that it flies, then we can conclude that it flies". A background theory containing some facts about birds is the following one:

W=\{\mathrm {Bird} (\mathrm {Condor} ),\mathrm {Bird} (\mathrm {Penguin} ),\neg \mathrm {Flies} (\mathrm {Penguin} ),\mathrm {Flies} (\mathrm {Bee} )\}

.

According to this default rule, a condor flies because the precondition $Bird(Condor)$ is true and the justification $Flies(Condor)$ is not inconsistent with what is currently known. On the contrary, $Bird(Penguin)$ does not allow concluding $Flies(Penguin)$ : even if the precondition of the default $Bird(Penguin)$ is true, the justification $Flies(Penguin)$ is inconsistent with what is known. From this background theory and this default, $Bird(Bee)$ cannot be concluded because the default rule only allows deriving $Flies(X)$ from $Bird(X)$ , but not vice versa. Deriving the antecedents of an inference rule from the consequences is a form of explanation of the consequences, and is the aim of abductive reasoning.

A common default assumption is that what is not known to be true is believed to be false. This is known as the Closed-World Assumption, and is formalized in default logic using a default like the following one for every fact $F$ .

{\frac {:{\neg }F}{{\neg }F}}

For example, the computer language Prolog uses a sort of default assumption when dealing with negation: if a negative atom cannot be proved to be true, then it is assumed to be false. Note, however, that Prolog uses the so-called negation as failure: when the interpreter has to evaluate the atom $\neg F$ , it tries to prove that $F$ is true, and conclude that $\neg F$ is true if it fails. In default logic, instead, a default having $\neg F$ as a justification can only be applied if $\neg F$ is consistent with the current knowledge.

Restrictions

A default is categorical or prerequisite-free if it has no prerequisite (or, equivalently, its prerequisite is tautological). A default is normal if it has a single justification that is equivalent to its conclusion. A default is supernormal if it is both categorical and normal. A default is seminormal if all its justifications entail its conclusion. A default theory is called categorical, normal, supernormal, or seminormal if all defaults it contains are categorical, normal, supernormal, or seminormal, respectively.

Semantics of default logic

A default rule can be applied to a theory if its precondition is entailed by the theory and its justifications are all consistent with the theory. The application of a default rule leads to the addition of its consequence to the theory. Other default rules may then be applied to the resulting theory. When the theory is such that no other default can be applied, the theory is called an extension of the default theory. The default rules may be applied in different order, and this may lead to different extensions. The Nixon diamond example is a default theory with two extensions:

\left\langle \left\{{\frac {\mathrm {Republican} (X):\neg \mathrm {Pacifist} (X)}{\neg \mathrm {Pacifist} (X)}},{\frac {\mathrm {Quaker} (X):\mathrm {Pacifist} (X)}{\mathrm {Pacifist} (X)}}\right\},\left\{\mathrm {Republican} (\mathrm {Nixon} ),\mathrm {Quaker} (\mathrm {Nixon} )\right\}\right\rangle

Since Nixon is both a Republican and a Quaker, both defaults can be applied. However, applying the first default leads to the conclusion that Nixon is not a pacifist, which makes the second default not applicable. In the same way, applying the second default we obtain that Nixon is a pacifist, thus making the first default not applicable. This particular default theory has therefore two extensions, one in which $Pacifist(Nixon)$ is true, and one in which $Pacifist(Nixon)$ is false.

The original semantics of default logic was based on the fixed point of a function. The following is an equivalent algorithmic definition. If a default contains formulae with free variables, it is considered to represent the set of all defaults obtained by giving a value to all these variables. A default ${\displaystyle {\frac {\alpha$ is applicable to a propositional theory $T$ if $T\models \alpha$ and all theories $T\cup \{\beta _{i}\}$ are consistent. The application of this default to $T$ leads to the theory $T\cup \{\gamma \}$ . An extension can be generated by applying the following algorithm:

T = W         /* current theory */ A = 0         /* set of defaults applied so far */                 /* apply a sequence of defaults */ while there is a default d that is not in A and is applicable to T     add the consequence of d to T     add d to A                 /* final consistency check */ iffor every default d in A         T is consistent with all justifications of d then     output T

This algorithm is non-deterministic, as several defaults can alternatively be applied to a given theory $T$ . In the Nixon diamond example, the application of the first default leads to a theory to which the second default cannot be applied and vice versa. As a result, two extensions are generated: one in which Nixon is a pacifist and one in which Nixon is not a pacifist.

The final check of consistency of the justifications of all defaults that have been applied implies that some theories do not have any extensions. In particular, this happens whenever this check fails for every possible sequence of applicable defaults. The following default theory has no extension:

\left\langle \left\{{\frac {:A(b)}{\neg A(b)}}\right\},\emptyset \right\rangle

Since $A(b)$ is consistent with the background theory, the default can be applied, thus leading to the conclusion that $A(b)$ is false. This result however undermines the assumption that has been made for applying the first default. Consequently, this theory has no extensions.

In a normal default theory, all defaults are normal: each default has the form ${\displaystyle {\frac {\phi$ . A normal default theory is guaranteed to have at least one extension. Furthermore, the extensions of a normal default theory are mutually inconsistent, i.e., inconsistent with each other.

Entailment

A default theory can have zero, one, or more extensions. Entailment of a formula from a default theory can be defined in two ways:

Skeptical: a formula is entailed by a default theory if it is entailed by all its extensions;

Credulous: a formula is entailed by a default theory if it is entailed by at least one of its extensions.

Thus, the Nixon diamond example theory has two extensions, one in which Nixon is a pacifist and one in which he is not a pacifist. Consequently, neither $Pacifist(Nixon)$ nor $\neg Pacifist(Nixon)$ are skeptically entailed, while both of them are credulously entailed. As this example shows, the credulous consequences of a default theory may be inconsistent with each other.

Alternative default inference rules

The following alternative inference rules for default logic are all based on the same syntax as the original system.

Justified: differs from the original one in that a default is not applied if thereby the set $T$ becomes inconsistent with a justification of an applied default;

Concise: a default is applied only if its consequence is not already entailed by $T$ (the exact definition is more complicated than this one; this is only the main idea behind it);

Constrained: a default is applied only if the set composed of the background theory, the justifications of all applied defaults, and the consequences of all applied defaults (including this one) is consistent;

Rational: similar to constrained default logic, but the consequence of the default to add is not considered in the consistency check;

Cautious: defaults that can be applied but are conflicting with each other (like the ones of the Nixon diamond example) are not applied.

The justified and constrained versions of the inference rule assign at least an extension to every default theory.

Variants of default logic

The following variants of default logic differ from the original one on both syntax and semantics.

Assertional variants: An assertion is a pair $\langle p:\{r_{1},\ldots ,r_{n}\}\rangle$ composed of a formula and a set of formulae. Such a pair indicates that $p$ is true while the formulae $r_{1},\ldots ,r_{n}$ have been assumed consistent to prove that $p$ is true. An assertional default theory is composed of an assertional theory (a set of assertional formulae) called the background theory and a set of defaults defined as in the original syntax. Whenever a default is applied to an assertional theory, the pair composed of its consequence and its set of justifications is added to the theory. The following semantics use assertional theories:

Cumulative default logic
Commitment to assumptions default logic
Quasi-default logic

Weak extensions: rather than checking whether the preconditions are valid in the theory composed of the background theory and the consequences of the applied defaults, the preconditions are checked for validity in the extension that will be generated; in other words, the algorithm for generating extensions starts by guessing a theory and using it in place of the background theory; what results from the process of extension generation is actually an extension only if it is equivalent to the theory guessed at the beginning. This variant of default logic is related in principle to autoepistemic logic, where a theory $\Box x\rightarrow x$ has the model in which $x$ is true just because, assuming $\Box x$ true, the formula $\Box x\rightarrow x$ supports the initial assumption.

Disjunctive default logic: the consequence of a default is a set of formulae instead of a single formula. Whenever the default is applied, at least one of its consequences is nondeterministically chosen and made true.

Priorities on defaults: the relative priority of defaults can be explicitly specified; among the defaults that are applicable to a theory, only one of the most preferred ones can be applied. Some semantics of default logic do not require priorities to be explicitly specified; rather, more specific defaults (those that are applicable in fewer cases) are preferred over less specific ones.

Statistical variant: a statistical default is a default with an attached upper bound on its frequency of error; in other words, the default is assumed to be an incorrect inference rule in at most that fraction of times it is applied.

Translations

Default theories can be translated into theories in other logics and vice versa. The following conditions on translations have been considered:

Consequence-Preserving: the original and the translated theories have the same (propositional) consequences;

Faithful: this condition only makes sense when translating between two variants of default logic or between default logic and a logic in which a concept similar to extension exists, e.g., models in modal logic; a translation is faithful if there exists a mapping (typically, a bijection) between the extensions (or models) of the original and translated theories;

Modular: a translation from default logic to another logic is modular if the defaults and the background theory can be translated separately; moreover, the addition of formulae to the background theory only leads to adding the new formulae to the result of the translation;

Same-Alphabet: the original and translated theories are built on the same alphabet;

Polynomial: the running time of the translation or the size of the generated theory are required to be polynomial in the size of the original theory.

Translations are typically required to be faithful or at least consequence-preserving, while the conditions of modularity and same alphabet are sometimes ignored.

The translatability between propositional default logic and the following logics have been studied:

classical propositional logic;
autoepistemic logic;
propositional default logic restricted to seminormal theories;
alternative semantics of default logic;
circumscription.

Translations exist or not depending on which conditions are imposed. Translations from propositional default logic to classical propositional logic cannot always generate a polynomially sized propositional theory, unless the polynomial hierarchy collapses. Translations to autoepistemic logic exist or not depending on whether modularity or the use of the same alphabet is required.

Complexity

The computational complexity of the following problems about default logic is known:

Existence of extensions: deciding whether a propositional default theory has at least one extension is $\Sigma _{2}^{P}$ -complete;

Skeptical entailment: deciding whether a propositional default theory skeptically entails a propositional formula is $\Pi _{2}^{P}$ -complete;

Credulous entailment: deciding whether a propositional default theory credulously entails a propositional formula is $\Sigma _{2}^{P}$ -complete;

Extension checking: deciding whether a propositional formula is equivalent to an extension of a propositional default theory is $\Delta _{2}^{P[\log ]}$ -complete;

Model checking: deciding whether a propositional interpretation is a model of an extension of a propositional default theory is $\Sigma _{2}^{P}$ -complete.

Implementations

Four systems implementing default logics are DeReS ^{[ permanent dead link ]}, XRay, GADeL Archived 2007-04-06 at the Wayback Machine , and Catala.

Related Research Articles

In artificial intelligence, with implications for cognitive science, the frame problem describes an issue with using first-order logic to express facts about a robot in the world. Representing the state of a robot with traditional first-order logic requires the use of many axioms that simply imply that things in the environment do not change arbitrarily. For example, Hayes describes a "block world" with rules about stacking blocks together. In a first-order logic system, additional axioms are required to make inferences about the environment. The frame problem is the problem of finding adequate collections of axioms for a viable description of a robot environment.

Propositional calculus is a branch of logic. It is also called propositional logic, statement logic, sentential calculus, sentential logic, or sometimes zeroth-order logic. It deals with propositions and relations between propositions, including the construction of arguments based on them. Compound propositions are formed by connecting propositions by logical connectives. Propositions that contain no logical connectives are called atomic propositions.

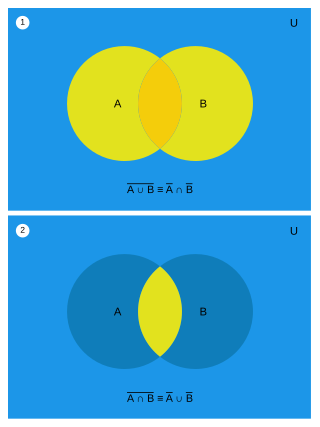
<span class="mw-page-title-main">De Morgan's laws</span> Pair of logical equivalences

In propositional logic and Boolean algebra, De Morgan's laws, also known as De Morgan's theorem, are a pair of transformation rules that are both valid rules of inference. They are named after Augustus De Morgan, a 19th-century British mathematician. The rules allow the expression of conjunctions and disjunctions purely in terms of each other via negation.

In Boolean logic, a formula is in conjunctive normal form (CNF) or clausal normal form if it is a conjunction of one or more clauses, where a clause is a disjunction of literals; otherwise put, it is a product of sums or an AND of ORs. As a canonical normal form, it is useful in automated theorem proving and circuit theory.

In traditional logic, a contradiction occurs when a proposition conflicts either with itself or established fact. It is often used as a tool to detect disingenuous beliefs and bias. Illustrating a general tendency in applied logic, Aristotle's law of noncontradiction states that "It is impossible that the same thing can at the same time both belong and not belong to the same object and in the same respect."

<span class="mw-page-title-main">Negation</span> Logical operation

In logic, negation, also called the logical not or logical complement, is an operation that takes a proposition $to another proposition "not ", standing for " is not true", written, or . It is interpreted intuitively as being true when is false, and false when is true. Negation is thus a unary logical connective. It may be applied as an operation on notions, propositions, truth values, or semantic values more generally. In classical logic, negation is normally identified with the truth function that takes truth to falsity . In intuitionistic logic, according to the Brouwer-Heyting-Kolmogorov interpretation, the negation of a proposition is the proposition whose proofs are the refutations of .$

Intuitionistic logic, sometimes more generally called constructive logic, refers to systems of symbolic logic that differ from the systems used for classical logic by more closely mirroring the notion of constructive proof. In particular, systems of intuitionistic logic do not assume the law of the excluded middle and double negation elimination, which are fundamental inference rules in classical logic.

In mathematics, constructive analysis is mathematical analysis done according to some principles of constructive mathematics.

In mathematical logic, sequent calculus is a style of formal logical argumentation in which every line of a proof is a conditional tautology instead of an unconditional tautology. Each conditional tautology is inferred from other conditional tautologies on earlier lines in a formal argument according to rules and procedures of inference, giving a better approximation to the natural style of deduction used by mathematicians than to David Hilbert's earlier style of formal logic, in which every line was an unconditional tautology. More subtle distinctions may exist; for example, propositions may implicitly depend upon non-logical axioms. In that case, sequents signify conditional theorems in a first-order language rather than conditional tautologies.

A paraconsistent logic is an attempt at a logical system to deal with contradictions in a discriminating way. Alternatively, paraconsistent logic is the subfield of logic that is concerned with studying and developing "inconsistency-tolerant" systems of logic, which reject the principle of explosion.

Computation tree logic (CTL) is a branching-time logic, meaning that its model of time is a tree-like structure in which the future is not determined; there are different paths in the future, any one of which might be an actual path that is realized. It is used in formal verification of software or hardware artifacts, typically by software applications known as model checkers, which determine if a given artifact possesses safety or liveness properties. For example, CTL can specify that when some initial condition is satisfied, then all possible executions of a program avoid some undesirable condition. In this example, the safety property could be verified by a model checker that explores all possible transitions out of program states satisfying the initial condition and ensures that all such executions satisfy the property. Computation tree logic belongs to a class of temporal logics that includes linear temporal logic (LTL). Although there are properties expressible only in CTL and properties expressible only in LTL, all properties expressible in either logic can also be expressed in CTL*.

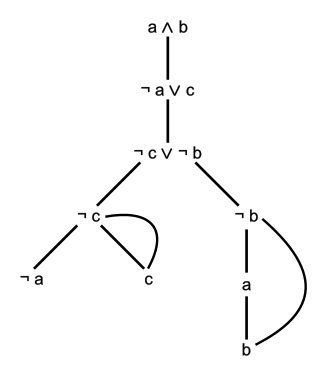
In proof theory, the semantic tableau is a decision procedure for sentential and related logics, and a proof procedure for formulae of first-order logic. An analytic tableau is a tree structure computed for a logical formula, having at each node a subformula of the original formula to be proved or refuted. Computation constructs this tree and uses it to prove or refute the whole formula. The tableau method can also determine the satisfiability of finite sets of formulas of various logics. It is the most popular proof procedure for modal logics.

Belief revision is the process of changing beliefs to take into account a new piece of information. The logical formalization of belief revision is researched in philosophy, in databases, and in artificial intelligence for the design of rational agents.

Negation as failure is a non-monotonic inference rule in logic programming, used to derive $from failure to derive . Note that can be different from the statement of the logical negation of, depending on the completeness of the inference algorithm and thus also on the formal logic system.$

The closed-world assumption (CWA), in a formal system of logic used for knowledge representation, is the presumption that a statement that is true is also known to be true. Therefore, conversely, what is not currently known to be true, is false. The same name also refers to a logical formalization of this assumption by Raymond Reiter. The opposite of the closed-world assumption is the open-world assumption (OWA), stating that lack of knowledge does not imply falsity. Decisions on CWA vs. OWA determine the understanding of the actual semantics of a conceptual expression with the same notations of concepts. A successful formalization of natural language semantics usually cannot avoid an explicit revelation of whether the implicit logical backgrounds are based on CWA or OWA.

In mathematical logic, Heyting arithmetic $is an axiomatization of arithmetic in accordance with the philosophy of intuitionism. It is named after Arend Heyting, who first proposed it.$

Circumscription is a non-monotonic logic created by John McCarthy to formalize the common sense assumption that things are as expected unless otherwise specified. Circumscription was later used by McCarthy in an attempt to solve the frame problem. To implement circumscription in its initial formulation, McCarthy augmented first-order logic to allow the minimization of the extension of some predicates, where the extension of a predicate is the set of tuples of values the predicate is true on. This minimization is similar to the closed-world assumption that what is not known to be true is false.

The autoepistemic logic is a formal logic for the representation and reasoning of knowledge about knowledge. While propositional logic can only express facts, autoepistemic logic can express knowledge and lack of knowledge about facts.

Epistemic modal logic is a subfield of modal logic that is concerned with reasoning about knowledge. While epistemology has a long philosophical tradition dating back to Ancient Greece, epistemic logic is a much more recent development with applications in many fields, including philosophy, theoretical computer science, artificial intelligence, economics and linguistics. While philosophers since Aristotle have discussed modal logic, and Medieval philosophers such as Avicenna, Ockham, and Duns Scotus developed many of their observations, it was C. I. Lewis who created the first symbolic and systematic approach to the topic, in 1912. It continued to mature as a field, reaching its modern form in 1963 with the work of Kripke.

Markov's principle, named after Andrey Markov Jr, is a conditional existence statement for which there are many equivalent formulations, as discussed below.

References

G. Antoniou (1999). A tutorial on default logics. ACM Computing Surveys, 31(4):337-359.
M. Cadoli, F. M. Donini, P. Liberatore, and M. Schaerf (2000). Space efficiency of propositional knowledge representation formalisms Archived 2013-05-09 at the Wayback Machine . Journal of Artificial Intelligence Research, 13:1-31.
P. Cholewinski, V. Marek, and M. Truszczynski (1996). Default reasoning system DeReS. In Proceedings of the Fifth International Conference on the Principles of Knowledge Representation and Reasoning (KR'96), pages 518-528.
J. Delgrande and T. Schaub (2003). On the relation between Reiter's default logic and its (major) variants. In Seventh European Conference on Symbolic and Quantitative Approaches to Reasoning with Uncertainty (ECSQARU 2003), pages 452-463.
J. P. Delgrande, T. Schaub, and W. K. Jackson (1994). Alternative approaches to default logic. Artificial Intelligence, 70:167-237.
G. Gottlob (1992). Complexity results for nonmonotonic logics. Journal of Logic and Computation, 2:397-425.
G. Gottlob (1995). Translating default logic into standard autoepistemic logic. Journal of the ACM, 42:711-740.
T. Imielinski (1987). Results on translating defaults to circumscription. Artificial Intelligence, 32:131-146.
T. Janhunen (1998). On the intertranslatability of autoepistemic, default and priority logics, and parallel circumscription. In Proceedings of the Sixth European Workshop on Logics in Artificial Intelligence (JELIA'98), pages 216-232.
T. Janhunen (2003). Evaluating the effect of semi-normality on the expressiveness of defaults. Artificial Intelligence, 144:233-250.
H. E. Kyburg and C-M. Teng (2006). Nonmonotonic Logic and Statistical Inference. Computational Intelligence, 22(1): 26-51.
P. Liberatore and M. Schaerf (1998). The complexity of model checking for propositional default logics. In Proceedings of the Thirteenth European Conference on Artificial Intelligence (ECAI'98), pages 18–22.
W. Lukaszewicz (1988). Considerations on default logic: an alternative approach. Computational Intelligence, 4(1):1-16.
W. Marek and M. Truszczynski (1993). Nonmonotonic Logics: Context-Dependent Reasoning. Springer.
A. Mikitiuk and M. Truszczynski (1995). Constrained and rational default logics. In Proceedings of the Fourteenth International Joint Conference on Artificial Intelligence (IJCAI'95), pages 1509-1517.
P. Nicolas, F. Saubion and I. Stéphan (2001). Heuristics for a Default Logic Reasoning System Archived 2017-09-07 at the Wayback Machine . International Journal on Artificial Intelligence Tools, 10(4):503-523.
R. Reiter (1980). A logic for default reasoning. Artificial Intelligence, 13:81-132.
T. Schaub, S. Brüning, and P. Nicolas (1996). XRay: A prolog technology theorem prover for default reasoning: A system description. In Proceedings of the Thirteenth International Conference on Automated Deduction (CADE'96), pages 293-297.
G. Wheeler (2004). A resource bounded default logic. In Proceedings of the 10th International Workshop on Non-Monotonic Reasoning (NMR-04), Whistler, British Columbia, 416-422.
G. Wheeler and C. Damasio (2004). An Implementation of Statistical Default Logic. In Proceedings of the 9th European Conference on Logics in Artificial Intelligence (JELIA 2004), LNCS Series, Springer, pages 121-133.

External links

Schmidt, Charles F. RCI.Rutgers.edu, Default Logic. Retrieved August 10, 2004.
Ramsay, Allan (1999). UMIST.ac.uk, Default Logic. Retrieved August 10, 2004.
Stanford.edu, Defeasible reasoning, Stanford Encyclopedia of Philosophy.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.