In mathematics, a root system is a configuration of vectors in a Euclidean space satisfying certain geometrical properties. The concept is fundamental in the theory of Lie groups and Lie algebras, especially the classification and representation theory of semisimple Lie algebras. Since Lie groups and Lie algebras have become important in many parts of mathematics during the twentieth century, the apparently special nature of root systems belies the number of areas in which they are applied. Further, the classification scheme for root systems, by Dynkin diagrams, occurs in parts of mathematics with no overt connection to Lie theory. Finally, root systems are important for their own sake, as in spectral graph theory.
In the mathematical field of representation theory, a weight of an algebra A over a field F is an algebra homomorphism from A to F, or equivalently, a one-dimensional representation of A over F. It is the algebra analogue of a multiplicative character of a group. The importance of the concept, however, stems from its application to representations of Lie algebras and hence also to representations of algebraic and Lie groups. In this context, a weight of a representation is a generalization of the notion of an eigenvalue, and the corresponding eigenspace is called a weight space.

In mathematics, G2 is three simple Lie groups (a complex form, a compact real form and a split real form), their Lie algebras as well as some algebraic groups. They are the smallest of the five exceptional simple Lie groups. G2 has rank 2 and dimension 14. It has two fundamental representations, with dimension 7 and 14.

In mathematics, in particular the theory of Lie algebras, the Weyl group of a root system Φ is a subgroup of the isometry group of that root system. Specifically, it is the subgroup which is generated by reflections through the hyperplanes orthogonal to at least one of the roots, and as such is a finite reflection group. In fact it turns out that most finite reflection groups are Weyl groups. Abstractly, Weyl groups are finite Coxeter groups, and are important examples of these.

In mathematics and theoretical physics, the term quantum group denotes one of a few different kinds of noncommutative algebras with additional structure. These include Drinfeld–Jimbo type quantum groups, compact matrix quantum groups, and bicrossproduct quantum groups. Despite their name, they do not themselves have a natural group structure, though they are in some sense 'close' to a group.

In transcendental number theory, the Lindemann–Weierstrass theorem is a result that is very useful in establishing the transcendence of numbers. It states the following:
The Gell-Mann matrices, developed by Murray Gell-Mann, are a set of eight linearly independent 3×3 traceless Hermitian matrices used in the study of the strong interaction in particle physics. They span the Lie algebra of the SU(3) group in the defining representation.

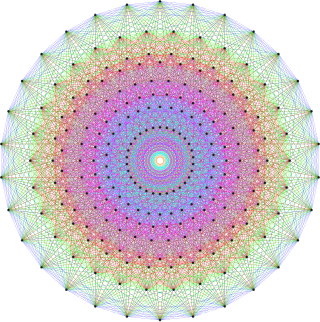
In mathematics, E8 is any of several closely related exceptional simple Lie groups, linear algebraic groups or Lie algebras of dimension 248; the same notation is used for the corresponding root lattice, which has rank 8. The designation E8 comes from the Cartan–Killing classification of the complex simple Lie algebras, which fall into four infinite series labeled An, Bn, Cn, Dn, and five exceptional cases labeled G2, F4, E6, E7, and E8. The E8 algebra is the largest and most complicated of these exceptional cases.

In mathematics, SO(8) is the special orthogonal group acting on eight-dimensional Euclidean space. It could be either a real or complex simple Lie group of rank 4 and dimension 28.
In mathematics, and specifically differential geometry, a connection form is a manner of organizing the data of a connection using the language of moving frames and differential forms.
In mathematics, a Kac–Moody algebra is a Lie algebra, usually infinite-dimensional, that can be defined by generators and relations through a generalized Cartan matrix. These algebras form a generalization of finite-dimensional semisimple Lie algebras, and many properties related to the structure of a Lie algebra such as its root system, irreducible representations, and connection to flag manifolds have natural analogues in the Kac–Moody setting.

In mathematics, a Lie algebra is semisimple if it is a direct sum of simple Lie algebras.
In mathematics, an affine Lie algebra is an infinite-dimensional Lie algebra that is constructed in a canonical fashion out of a finite-dimensional simple Lie algebra. Given an affine Lie algebra, one can also form the associated affine Kac-Moody algebra, as described below. From a purely mathematical point of view, affine Lie algebras are interesting because their representation theory, like representation theory of finite-dimensional semisimple Lie algebras, is much better understood than that of general Kac–Moody algebras. As observed by Victor Kac, the character formula for representations of affine Lie algebras implies certain combinatorial identities, the Macdonald identities.
In theoretical physics and mathematics, a Wess–Zumino–Witten (WZW) model, also called a Wess–Zumino–Novikov–Witten model, is a type of two-dimensional conformal field theory named after Julius Wess, Bruno Zumino, Sergei Novikov and Edward Witten. A WZW model is associated to a Lie group, and its symmetry algebra is the affine Lie algebra built from the corresponding Lie algebra. By extension, the name WZW model is sometimes used for any conformal field theory whose symmetry algebra is an affine Lie algebra.
In mathematics, the Weyl character formula in representation theory describes the characters of irreducible representations of compact Lie groups in terms of their highest weights. It was proved by Hermann Weyl. There is a closely related formula for the character of an irreducible representation of a semisimple Lie algebra. In Weyl's approach to the representation theory of connected compact Lie groups, the proof of the character formula is a key step in proving that every dominant integral element actually arises as the highest weight of some irreducible representation. Important consequences of the character formula are the Weyl dimension formula and the Kostant multiplicity formula.
In mathematics, the Harish-Chandra isomorphism, introduced by Harish-Chandra , is an isomorphism of commutative rings constructed in the theory of Lie algebras. The isomorphism maps the center of the universal enveloping algebra of a reductive Lie algebra to the elements of the symmetric algebra of a Cartan subalgebra that are invariant under the Weyl group .
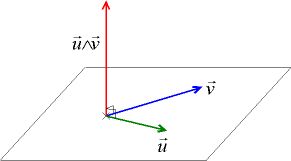
In mathematics, the structure constants or structure coefficients of an algebra over a field are the coefficients of the basis expansion of the products of basis vectors. Because the product operation in the algebra is bilinear, by linearity knowing the product of basis vectors allows to compute the product of any elements . Therefore, the structure constants can be used to specify the product operation of the algebra. Given the structure constants, the resulting product is obtained by bilinearity and can be uniquely extended to all vectors in the vector space, thus uniquely determining the product for the algebra.
In mathematical physics, nonlinear realization of a Lie group G possessing a Cartan subgroup H is a particular induced representation of G. In fact, it is a representation of a Lie algebra of G in a neighborhood of its origin. A nonlinear realization, when restricted to the subgroup H reduces to a linear representation.

This is a glossary for the terminology applied in the mathematical theories of Lie groups and Lie algebras. For the topics in the representation theory of Lie groups and Lie algebras, see Glossary of representation theory. Because of the lack of other options, the glossary also includes some generalizations such as quantum group.
The Infeld–Van der Waerden symbols, sometimes called simply Van der Waerden symbols, are an invariant symbol associated to the Lorentz group used in quantum field theory. They are named after Leopold Infeld and Bartel Leendert van der Waerden.



























