தனி மதிப்பு

கணிதத்தில் ஓர் மெய்யெண்ணின் தனிமதிப்பு (absolute value) அல்லது மட்டுமதிப்பு (modulus) என்பது அந்த எண்ணை நேர்மறை எதிர்மறை பாகுபாடின்றி கருதுதல் ஆகும். ஒரு மெய்யெண்ணின் தனிமதிப்பு அதன் எதிரில்லா மதிப்பாகும். பூச்சியத்திலிருந்து ஓர் எண்ணின் தொலைவாக அந்த எண்ணின் தனிமதிப்பைக் கொள்ளலாம். x ஒரு மெய்யெண் எனில்,
- x நேர் எண் எனில் | x | = x
- x எதிர் எண் எனில் | x | = - x
- |0| = 0.
எடுத்துக்காட்டாக, |3| = 3 ; |-3| = - (-3) = 3.
தனிமதிப்பானது மெய்யெண்களுக்கு மட்டுமல்லாது சிக்கலெண்கள், வளையங்கள், களங்கள், திசையன் வெளிகளுக்கும் வரையறுக்கப்படுகிறது.
சொல்லியலும் குறியீடும்
[தொகு]1806 ஆம் ஆண்டில் ஜீன்-ராபர்ட் ஆர்கண்ட் எனும் கணிதவியலாளரால் அளவின் அலகு எனப் பிரெஞ்சு மொழியில் பொருள்படும் மாடூல் ("module") என்ற சொல்லை சிக்கலெண்ணின் தனிமதிப்பைக் குறிப்பதற்கு அறிமுகப்படுத்தினார்.[1][2] 1866 ஆம் ஆண்டில் இவ்வார்த்தை ஆங்கிலத்தில் மாடுலஸ் ("modulus") என்ற லத்தீன் வார்த்தையாகப் பயன்படுத்தப்பட்டது.[1] குறியீடு |x|, 1841 இல் ஜெர்மானிய கணிதவியலாளர் கார்ல் வியர்ஸ்ட்ரசால் அறிமுகப்படுத்தப்பட்டது.[3] எண்ணளவு அல்லது எண் மதிப்பு எனவும் தனிமதிப்பு அழைக்கப்படுகிறது.[1]
வரையறையும் பண்புகளும்
[தொகு]மெய்யெண்கள்
[தொகு]ஏதேனுமொரு மெய்யெண் x இன் தனிமதிப்பு அல்லது மட்டுமதிப்பின் குறியீடு: |x|. அதன் வரையறை [4]:
இந்த வரையறையிலிருந்து ஒரு மெய்யெண்ணின் தனிமதிப்பு நேர் மதிப்பாகவோ அல்லது பூச்சியமாகவோத்தான் இருக்குமே தவிர ஒருபோதும் எதிர் மதிப்பாக இருக்காது என்பதைக் காணலாம்.
பகுமுறை வடிவவியல்படி, ஒரு மெய்யெண்ணின் தனிமதிப்பு என்பது மெய்யெண்கோட்டில் பூச்சியத்திலிருந்து அந்த எண் அமையும் தொலைவைக் குறிக்கும்; இரு மெய்யெண்களின் வித்தியாசத்தின் தனிமதிப்பு அவ்விரு எண்களுக்கிடையே உள்ள தொலைவைக் குறிக்கும். குறியில்லா வர்க்கமூலக் குறியீடு நேர் வர்க்கமூலத்தைக் குறிப்பதால்,
(1)
இதுவே சில சமயங்களில் தனிமதிப்பை வரையறுக்கவும் பயன்படுத்தப்படுகிறது.[5]
தனிமதிப்பிற்குப் பின்வரும் நான்கு அடிப்படைப் பண்புகள் உள்ளன:
(2) (3) (4) (5)
பிற பண்புகள்:
(6) (7) (8) (9) (if ) (10) (11) (12) அல்லது (13)
கடைசி இரண்டு அசமன்பாடுகளைக் பயன்படுத்தி கீழ்க்காணும் கணக்கைத் தீர்க்கலாம்:
சிக்கலெண்கள்
[தொகு]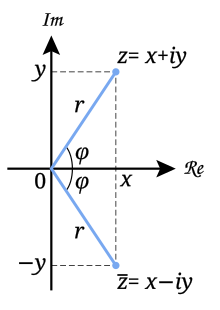
சிக்கலெண்களை வரிசைப்படுத்த முடியாதென்பதால், மெய்யெண்களின் தனிமதிப்பு வரையறையை நேரிடையாகச் சிக்கலெண்களுக்கு நீட்டிக்க முடியாது. எனினும் ஒரு மெய்யெண்ணின் தனிமதிப்பு என்பது மெய்யெண்கோட்டில் பூச்சியத்திலிருந்து அந்த எண் அமையும் தொலைவைக் குறிக்கும் என்ற கருத்தை சிக்கலெண்களுக்கு நீட்டிக்கலாம். ஒரு சிக்கலெண்ணின் தனிமதிப்பானது, சிக்கலெண் தளத்தில் ஆதிப்புள்ளியிலிருந்து அச்சிக்கலெண்ணின் தொலைவைக் குறிக்கும்; இரு சிக்கலெண்களின் வித்தியாசத்தின் தனிமதிப்பு அவ்விரு சிக்கலெண்களுக்கு இடையேயுள்ள தொலைவைக் குறிக்கும்.
- , (x, y மெய்யெண்கள்) என்ற சிக்கலெண்ணின் தனிமதிப்பு அல்லது மட்டு மதிப்பின் குறியீடு |z|.
- [6]
இச்சிக்கலெண்ணின் கற்பனைப் பகுதி y இன் மதிப்பு பூச்சியமெனில்:
சிக்கலெண் போலார் ஆள்கூற்று முறைமையில் தரப்பட்டால்:
- (r ≥ 0, θ மெய்)
- .
சிக்கலெண்ணின் தனிமதிப்பைக் கீழ்க்காணும் முறையிலும் காணலாம்:
இங்கு இன் இணையியச் சிக்கலெண்
மேலே தரப்பட்டுள்ள மெய்யெண்களின் தனிமதிப்பின் பண்புகள் (2)–(11) சிக்கலெண்களின் தனிமதிப்பிற்கும் பொருந்தும்.
தனிமதிப்புச் சார்பு
[தொகு]
மெய்யெண்களின் தனிமதிப்புச் சார்பு எங்கும் ஒரு தொடர்ச்சியான சார்பு. பூச்சியம் தவிர்த்த அனைத்து மெய்யெண்களுக்கும் இச்சார்பு வகையிடத்தக்கது. (−∞, 0] இடைவெளியில் ஓரியல்பாகக் குறையும் சார்பாகவும் [0, ∞) இடைவெளியில் ஓரியல்பாகக் கூடும் சார்பாகவும் அமையும். ஒரு மெய்யெண்ணின் தனிமதிப்பும் அம்மெய்யெண்ணின் எதிர் மெய்யெண்ணின் தனிமதிப்பும் சமம் என்பதால் மெய்யெண்ணின் தனிமதிப்புச் சார்பு ஓர் இரட்டைச் சார்பு. எனவே இச்சார்பு நேர்மாற்றத்தக்கதல்ல. மேலும் இச்சார்பு துண்டுவாரி நேரியல் சார்பு மற்றும் குவிவுச் சார்பு.
மெய் மற்றும் சிக்கலெண் தனிமதிப்புச் சார்புகள் தன்னடுக்கானவை. ()
குறிச்சார்புடன் தொடர்பு
[தொகு]தனிமதிப்புச் சார்பு ஒரு மெய்யெண்ணின் மதிப்பை மட்டுமே தருகிறது; குறியினை விட்டுவிடுகிறது. ஆனால் குறிச் சார்பு மதிப்பை விட்டுவிட்டு குறியை மட்டுமே தருகிறது. இவ்விரு சார்புகளுக்கு இடையேயுள்ள தொடர்பு:
x ≠ 0 எனில்,
வகைக்கெழு
[தொகு]x ≠ 0 ஐத்தவிர மற்ற அனைத்து மெய்யெண்களுக்கும் தனிமதிப்புச் சார்பு வகையிடத்தக்கது. x ≠ 0 இல் இதன் வகைக்கெழு படிநிலைச் சார்பாகக் கிடைக்கும்.[7][8]
|x| இன் x ஐப் பொறுத்த இரண்டாம் வகைக்கெழு எங்கும் (பூச்சியத்தைத் தவிர) பூச்சியமாக இருக்கும்.
எதிர்வகைக்கெழு
[தொகு]தனிமதிப்புச் சார்பின் எதிர்வகைக்கெழு:
இங்கு C, தொகையீட்டுக் காரணி.
தொலைவு
[தொகு]தனிமதிப்பு என்னும் கருத்து, தொலைவுடன் நெருங்கிய தொடர்புடையது. ஒரு சிக்கலெண் அல்லது மெய்யெண்ணின் தனிமதிப்பானது சிக்கலெண் தளத்தில் ஆதிப்புள்ளிக்கும் அந்த சிக்கலென்ணுக்கும் இடைப்பட்ட தொலைவாகவும், மெய்யெண் கோட்டில் பூச்சியத்திற்கும் அந்த மெய்யெண்ணுக்கும் இடைப்பட்ட தொலைவாகவும் உள்ளது. மேலும் இரு சிக்கலெண்கள் அல்லது மெய்யெண்களின் வித்தியாசத்தின் தனிமதிப்பு அவ்விரு எண்களுக்கு இடைப்பட்டத் தொலைவைக் குறிக்கிறது.
இரு புள்ளிகளுக்கு இடைப்பட்ட யூக்ளிடிய தொலைவு:
யூக்ளிய n-வெளியில்
- எனும் இரு புள்ளிகளுக்கு இடைப்பட்ட தொலைவின் வரையறை:
இது |a − b| இன் பொதுமைப்படுத்தலாகிறது. ஏனெனில் a மற்றும் b மெய்யெண்களெனில் சமன்பாடு (1) இன் படி
- எனும் சிக்கலெண்கள் எனில்
எனவே மெய்யெண்களுக்கும் சிக்கலெண்களுக்கும் தனிமதிப்பு தரும் தொலைவு, ஒரு பரிமாண வெளி மற்றும் இருபரிமாண யூக்ளிடிய தொலைவுடன் ஒத்துள்ளது.
இரு சிக்கலெண்கள் அல்லது மெய்யெண்களின் வித்தியாசத்தின் தனிமதிப்பின் பண்புகளைக் கொண்டு தொலைவுச் சார்பை பின்வருமாறு வரையறுக்கலாம்:
X × X என்ற கணத்தின் மீது வரையறுக்கப்பட்ட மெய்ய்மதிப்புச் சார்பு d, பின்வரும் நான்கு அடிக்கோள்கள் நிறைவு செய்தால் தொலைவுச் சார்பு எனப்படும்:[9]
எதிரல்லாத்தன்மை (Non-negativity) தெளிவற்ற முற்றொருமை (Identity of indiscernibles) சமச்சீர் (Symmetry) முக்கோண சமனின்மை (Triangle inequality)
பொதுமைப்படுத்தல்
[தொகு]வரிசைப்படுத்தப்பட்ட வளையங்கள்
[தொகு]மேலே தரப்பட்ட மெய்யெண்களுக்கான தனிமதிப்பு வரையறையை வரிசைப்படுத்தப்பட்ட வளையங்களுக்கும் நீட்டிக்கலாம். வரிசைப்படுத்தப்பட்ட வளையம் R இன் ஓர் உறுப்பு a. அதன் தனிமதிப்பின் குறியீடு |a|. மேலும் அதன் வரையறை:[10]
இங்கு −a என்பது a இன் கூட்டல் நேர்மாறு; 0, கூட்டல் முற்றொருமை.
களங்கள்
[தொகு]மெய்யெண்களின் தனிமதிப்பின் அடிப்படைப் பண்புகளான சமன்பாடுகள் (2)–(5) ஐப் பயன்படுத்தி எந்தவொரு களத்திலும் தனிமதிப்பு என்னும் கருத்தை விளக்கலாம்.
களம் F இல் வரையறுக்கப்பட்ட ஒரு மெய்மதிப்புச் சார்பு v கீழுள்ள நான்கு எடுகோள்களை நிறைவு செய்தால் தனிமதிப்புச் சார்பு அல்லது மட்டுமதிப்பு அல்லது எண்ணளவு அல்லது மதிப்பு அல்லது மதிப்பீடு எனப்படும்:
இங்கு 0 களத்தின் கூட்டல் முற்றொருமை; 1 பெருக்கல் முற்றொருமை.
குறிப்புகள்
[தொகு]- ↑ 1.0 1.1 1.2 Oxford English Dictionary, Draft Revision, June 2008
- ↑ Nahin, O'Connor and Robertson, and functions.Wolfram.com.; for the French sense, see Littré, 1877
- ↑ Nicholas J. Higham, Handbook of writing for the mathematical sciences, SIAM. பன்னாட்டுத் தரப்புத்தக எண் 0-89871-420-6, p. 25
- ↑ Mendelson, p. 2.
- ↑ Stewart, James B. (2001). Calculus: concepts and contexts. Australia: Brooks/Cole. பன்னாட்டுத் தரப்புத்தக எண் 0-534-37718-1.
{{cite book}}: Cite has empty unknown parameter:|coauthors=(help), p. A5 - ↑ González, Mario O. (1992). Classical Complex Analysis. CRC Press. p. 19. பன்னாட்டுத் தரப்புத்தக எண் 9780824784157.
- ↑ Weisstein, Eric W. Absolute Value. From MathWorld – A Wolfram Web Resource.
- ↑ Bartel and Sherbert, p. 163
- ↑ இவை குறைந்தபட்சத் தேவையானவை அல்ல; ஏனென்றால் எதிரல்லாத்தன்மை அடிக்கோளை மற்ற மூன்று அடிக்கோள்களில் இருந்து பெற முடியும்: 0 = d(a, a) ≤ d(a, b) + d(b, a) = 2d(a, b).
- ↑ Mac Lane, p. 264.
மேற்கோள்கள்
[தொகு]- Bartle; Sherbert; Introduction to real analysis (4th ed.), John Wiley & Sons, 2011 பன்னாட்டுத் தரப்புத்தக எண் 978-0-471-43331-6.
- Nahin, Paul J.; An Imaginary Tale; Princeton University Press; (hardcover, 1998). பன்னாட்டுத் தரப்புத்தக எண் 0-691-02795-1.
- Mac Lane, Saunders, Garrett Birkhoff, Algebra, American Mathematical Soc., 1999. பன்னாட்டுத் தரப்புத்தக எண் 978-0-8218-1646-2.
- Mendelson, Elliott, Schaum's Outline of Beginning Calculus, McGraw-Hill Professional, 2008. பன்னாட்டுத் தரப்புத்தக எண் 978-0-07-148754-2.
- O'Connor, J.J. and Robertson, E.F.; "Jean Robert Argand".
- Schechter, Eric; Handbook of Analysis and Its Foundations, pp. 259–263, "Absolute Values", Academic Press (1997) பன்னாட்டுத் தரப்புத்தக எண் 0-12-622760-8.
வெளி இணைப்புகள்
[தொகு]- Hazewinkel, Michiel, ed. (2001), "Absolute value", Encyclopedia of Mathematics, Springer, பன்னாட்டுத் தரப்புத்தக எண் 978-1556080104
- absolute value at PlanetMath.
- Weisstein, Eric W., "Absolute Value", MathWorld.




















































