Skip to main content
PMC home page
Radiology: Cardiothoracic Imaging logoLink to Radiology: Cardiothoracic Imaging
. 2021 Jun 24;3(3):e200580. doi: 10.1148/ryct.2021200580

Accelerated in Vivo Cardiac Diffusion-Tensor MRI Using Residual Deep Learning–based Denoising in Participants with Obesity

Kellie Phipps 1, Maaike van de Boomen 1, Robert Eder 1, Sam Allen Michelhaugh 1, Aferdita Spahillari 1, Joan Kim 1, Shestruma Parajuli 1, Timothy G Reese 1, Choukri Mekkaoui 1, Saumya Das 1, Denise Gee 1, Ravi Shah 1, David E Sosnovik 1, Christopher Nguyen 1,✉
PMCID: PMC8259662  PMID: 34250491

Abstract

Purpose

To develop and assess a residual deep learning algorithm to accelerate in vivo cardiac diffusion-tensor MRI (DT-MRI) by reducing the number of averages while preserving image quality and DT-MRI parameters.

Materials and Methods

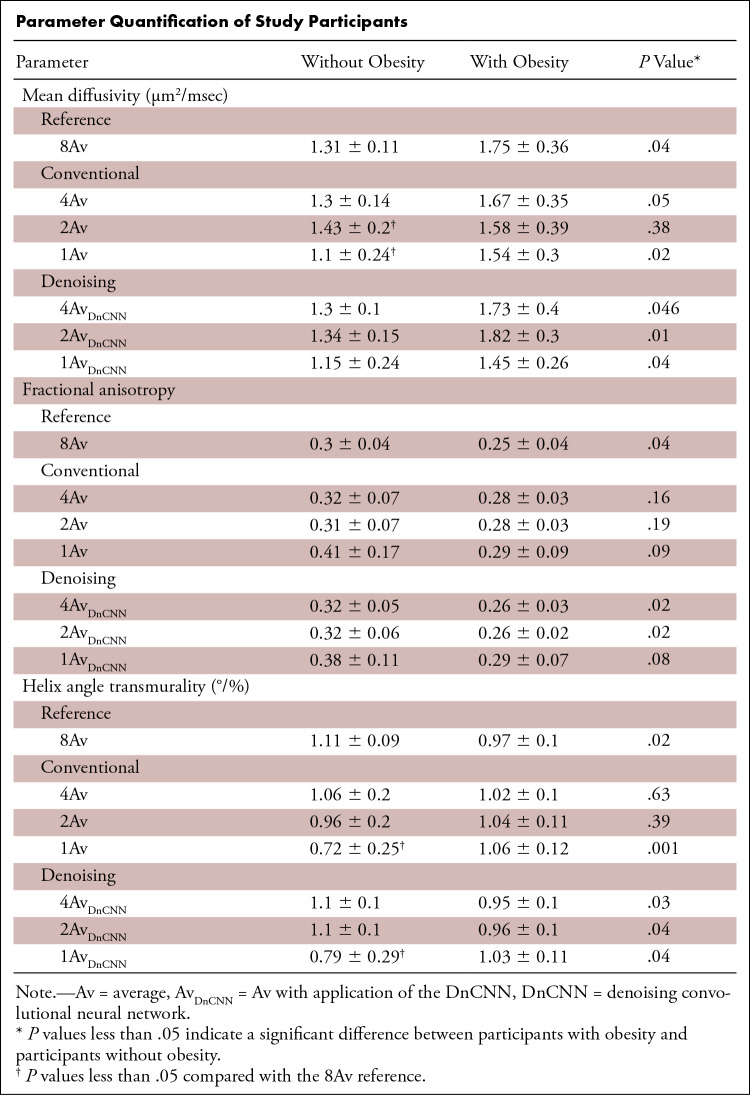
In this prospective study, a denoising convolutional neural network (DnCNN) for DT-MRI was developed; a total of 26 participants, including 20 without obesity (body mass index [BMI] < 30 kg/m2; mean age, 28 years ± 3 [standard deviation]; 11 women) and six with obesity (BMI ≥ 30 kg/m2; mean age, 48 years ± 11; five women), were recruited from June 19, 2019, to July 29, 2020. DT-MRI data were constructed at four averages (4Av), two averages (2Av), and one average (1Av) without and with the application of the DnCNN (4AvDnCNN, 2AvDnCNN, 1AvDnCNN). All data were compared against the reference DT-MRI data constructed at eight averages (8Av). Image quality, characterized by using the signal-to-noise ratio (SNR) and structural similarity index (SSIM), and the DT-MRI parameters of mean diffusivity (MD), fractional anisotropy (FA), and helix angle transmurality (HAT) were quantified.

Results

No differences were found in image quality or DT-MRI parameters between the accelerated 4AvDnCNN DT-MRI and the reference 8Av DT-MRI data for the SNR (29.1 ± 2.7 vs 30.5 ± 2.9), SSIM (0.97 ± 0.01), MD (1.3 µm2/msec ± 0.1 vs 1.31 µm2/msec ± 0.11), FA (0.32 ± 0.05 vs 0.30 ± 0.04), or HAT (1.10°/% ± 0.13 vs 1.11°/% ± 0.09). The relationship of a higher MD and lower FA and HAT in individuals with obesity compared with individuals without obesity in reference 8Av DT-MRI measurements was retained in 4AvDnCNN and 2AvDnCNN DT-MRI measurements but was not retained in 4Av or 2Av DT-MRI measurements.

Conclusion

Cardiac DT-MRI can be performed at an at least twofold-accelerated rate by using DnCNN to preserve image quality and DT-MRI parameter quantification.

Keywords: Adults, Cardiac, Obesity, Technology Assessment, MR-Diffusion Tensor Imaging, Heart, Tissue Characterization

Supplemental material is available for this article.

© RSNA, 2021

Keywords: Adults, Cardiac, Obesity, Technology Assessment, MR-Diffusion Tensor Imaging, Heart, Tissue Characterization

Summary

A deep learning denoising algorithm was developed to accelerate diffusion-tensor MRI (DT-MRI) data acquisition to preserve image quality and cardiac DT-MRI parameter quantification.

Key Points

  • ■ In vivo cardiac diffusion-tensor MRI (DT-MRI) using a residual deep learning denoising convolutional neural network (DnCNN) yielded image quality (in terms of signal-to-noise ratio [SNR] and structural similarity index measures) and DT-MRI parameters (mean diffusivity [MD], fractional anisotropy [FA], and helix angle transmurality [HAT]) that were comparable with those of standard cardiac DT-MRI but were achieved in half the scan time.

  • ■ Twofold-accelerated cardiac DT-MRI using a DnCNN preserved differences between participant groups with and without obesity for MD (1.73 μm2/msec ± 0.4 vs 1.3 μm2/msec ± 0.1; P = .046), FA (0.26 ± 0.03 vs 0.32 ± 0.05; P = .02), and HAT (0.95°/% ± 0.1 vs 1.1°/% ± 0.1; P = .03), while also preserving the image quality of standard DT-MRI at eight averages (8Av).

  • ■ Fourfold-accelerated cardiac DT-MRI using a DnCNN preserved differences between participant groups with and without obesity for MD (1.82 μm2/msec ± 0.3 vs 1.3 μm2/msec ± 0.15; P = .01), FA (0.26 ± 0.02 vs 0.32 ± 0.06; P = .02), and HAT (0.96°/% ± 0.1 vs 1.1°/% ± 0.1; P = .04); however, there was a reduction in the SNR compared with 8Av DT-MRI data (20.3 ± 2.1 vs 30.5 ± 2.9; P < .001).

Introduction

Obesity is a risk factor for heart failure and atrial fibrillation and is associated with left ventricular hypertrophy and myocardial fibrosis (1–6). Early, noninvasive tissue characterization using microstructural phenotyping of cardiac remodeling may provide early risk stratification and improved clinical management and outcomes (5,6). Cardiac diffusion-tensor MRI (DT-MRI) offers a noninvasive, contrast agent–free in vivo imaging approach that enables characterization of the myocardial microstructure and cardiomyocyte architecture. Recently, DT-MRI has been used to assess the myocardial microstructure in myocardial infarction (7), heart failure (8), cardiomyopathy (9), and even myocardial regeneration (10,11), demonstrating distinct and complementary prognostic value in predicting maladaptive myocardial function remodeling. However, in vivo DT-MRI of the heart is a signal-to-noise ratio (SNR)–constrained technique because the diffusion contrast relies on signal decay in addition to the short myocardial T2 relaxation time (12). This is especially challenging in patients with obesity because of the lack of proximity of the surface coil to the heart, which reduces the overall signal.

The use of signal averaging to improve SNR is inherently inefficient and can result in impractically long scan times, limiting clinical translation. Alternatively, standard denoising techniques based on smoothing or low-pass filtering can improve the SNR but involve an unacceptable loss in spatial resolution (13–16). An appealing alternative involves the use of neural networks, which have been used previously to improve medical imaging reconstruction of undersampled data to suppress high-frequency artifacts and noise (17–19). Classic image denoising approaches try to impose prior knowledge about the noise-free image through regularization within iterative reconstruction methods (13–16,20). More recently, deep learning methods have been designed to enable the incorporation of previously learned information from other collections of data and noise. These methods use regular residual networks (convolutional neural networks [CNNs]) to learn properties of the images to be denoised (21). To extend and combine these concepts, we further developed and rigorously tested a residual deep learning denoising CNN (DnCNN) (22) designed to identify the spatial distribution of noise from the diffusion-weighted images to denoise in vivo cardiac DT-MRI data. Although this proposed DnCNN was originally developed for color photography, we hypothesized that it could be successfully applied to cardiac diffusion-weighted images to improve the SNR by removing non-Gaussian noise while preserving detailed image features, such as edges and contrast. Furthermore, because this DnCNN was trained on acquired noise images as opposed to high-SNR or denoised images, it can more easily be acquired at reasonable scale (>1000 images) for robust machine learning.

We hypothesized that denoising in vivo DT-MRI acquisitions with DnCNN (DnCNN DT-MRI) would result in fewer needed signal averages, which would reduce scan time while potentially preserving key image features and quantification of DT-MRI parameters. Therefore, we compared DT-MRI data acquired at various averages with and without DnCNN with reference images acquired at eight averages (8Av) with a second-order motion-compensated DT-MRI (23–25) technique to determine the optimal achievable time reduction. For this comparison, the trade-off between scan acceleration and image quality and accurate quantification of DT-MRI parameters, including the mean diffusivity (MD), fractional anisotropy (FA), helix angle (HA), and HA transmurality (HAT), were evaluated.

Materials and Methods

Informed written consent was obtained from all participants in compliance with the Health Insurance Portability and Accountability Act and the hospital’s internal review boards (2015P002346 and 2016P00674).

Study Participants

The prospectively recruited study population consisted of two groups: 20 participants without obesity (body mass index [BMI] < 30 kg/m2) (10 for training data [seven women] and 10 for evaluation [six men]) and six participants with obesity (BMI ≥ 30 kg/m2; five women). Recruitment was performed on a volunteer basis from June 19, 2019, to July 29, 2020, in a consecutive series. Eligibility criteria included age older than 18 years, obesity (BMI ≥ 30 kg/m2; for obesity or bariatric surgery group) and nonobesity (BMI < 30 kg/m2; for control group), and provision of written informed consent. Major exclusion criteria included pregnancy, claustrophobia, contraindication to MRI, and prior cardiovascular disease, hypertension, or diabetes. An additional participant with obesity (BMI of 32.8 kg/m2) and chronic myocardial infarction was later included to test the DnCNN’s ability in participants with cardiac morphologic characteristics (Fig E1 [supplement]).

In Vivo Cardiac DT-MRI

In vivo second-order motion-compensated cardiac DT-MR spin-echo planar imaging of the whole left ventricle (repetition time, 12–R-R interval; echo time, 75 msec; 2.5 × 2.5 × 8 mm3; 12 sections; b = 50, 500 sec/mm2; 12 directions; 8Av [approximately 20 minutes], four averages [4Av; approximately 10 minutes], two averages [2Av; approximately 5 minutes], and one average [1Av; approximately 2.5 minutes] [23,24]) was performed on all 20 participants without obesity and the six participants with obesity by using a clinical 3-T system (Prisma; Siemens). Participants were scanned under free-breathing conditions, with electrocardiographic triggering coupled with multitasking-based motion correction to compensate for respiratory shifts (26). In addition, standard clinical cine imaging (True FISP two-dimensional sequence [Siemens]; repetition time, 43.16 msec; echo time, 1.46 msec; flip angle, 60°; 1.5 × 1.5 × 8 mm3) was performed in the participant groups with and without obesity to estimate cardiac function by using Segment version 3.0 software. Noise was identified with DnCNN and extracted from each single image and then combined into 2AvDnCNN, 4AvDnCNN, and 8AvDnCNN images. Furthermore, an additional noise image was acquired for each participant by using a DT-MRI acquisition with both b = 50 and b = 500 weighting and the radiofrequency turned off (ie, no spin excitation, but diffusion and imaging gradients were played), resulting in 2304 noise-image pairs (12 sections × 12 directions × 8Av).

Architecture and Training of the DnCNN

The DnCNN was trained to identify and output the residual noise image from acquired diffusion-weighted images from the scanner. Afterward, this output noise image was subtracted from the original input image, resulting in the desired denoised image (Fig 1). For training on images in 10 participants without obesity, high-SNR, diffusion-weighted images acquired at 8Av at 12 different section locations from 12 different diffusion directions using b = 50 and b = 500 weighting were used as reference signal images with magnitude r and phase Ø. Acquired complex noise data (nreal and nimag) were added to the reference signal images by using the following equation:

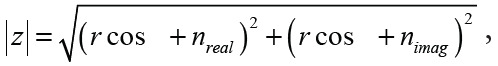graphic file with name ryct.2021200580.eq1.jpg

which resulted in a total of 23 040 input training images (|z|). The magnitude of the aforementioned noise images Inline graphic was then paired with the input training images to create a final 23 040-image data set to train the DnCNN with a cross-validation ratio of 80%–20% (20 epochs, momentum = 0.9, learning rate = 0.1, L2 regularization = 10–4). The cross-validation method used 20% of the 23 040-image training data set as the test data, to which the proposed DnCNN was completely blinded, and that were used purely for evaluation. The peak SNR (PSNR) was calculated at each iteration and epoch to quantify the improvement of the DnCNN throughout the training process and check for potential overfitting with the cross-validation test data set. Overfitting was determined to have occurred if the PSNR stopped monotonically increasing in the cross-validation curve (ie, a decrease in the PSNR after a steady monotonic increase). PSNR was calculated by using the following equation:

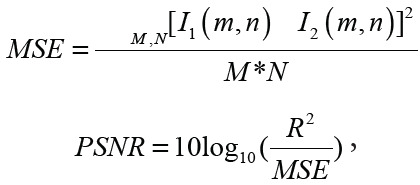graphic file with name ryct.2021200580.eq3.jpg

where M and N are the number of rows and columns of the input image, I1 and I2 are the ground truth image and the current image at a given iteration, respectively, and R is the maximum variation in the input image data type (eg, the unsigned integer is 255). Processing a single image took 32 msec when using a graphics processing unit and 80 msec when using a central processing unit, resulting in 74 seconds for 4Av data.

Figure 1:

(A) The data set of 23 040 input and output images used for training and testing the proposed denoising convolutional neural network (DnCNN) comprises 10 reference eight-average diffusion-weighted image (DWI) data sets (12 sections, 12 directions [Dir], b = 50, and b = 500) and 2304 complex noise input-output pairs. Complex noise images were acquired using the same diffusion-tensor MRI (DT-MRI) sequence but with radiofrequency excitation turned off. (B) Architecture of the proposed residual deep learning DnCNN consisting of a series of 56 layers of convolution (Conv), batch normalization (Batch Norm), and rectified linear unit (ReLU) operations. Stride and padding parameters were set to [1 1] and [1 1 1 1], respectively. The purpose of the DnCNN is to estimate the residual error (or unwanted noise) from a noisy signal by employing convolutional layers and subsequently using Batch Norm for fast and stable training that may arise from ill-poised initialization and changes in distributions of internal nonlinearity. The resulting output residual image in the denoising context is the “noise image,” which can be removed subsequently by simple subtraction. Thus, for this application of the DnCNN to in vivo cardiac DT-MRI, the input of the DnCNN is acquired single-average (signal + noise) DWIs, and the output results in estimated noise images. (C) Representative example of showing a single average raw DWI b = 50 image being denoised with a comparison with a reference eight-average DWI. First, the input single-average data are fed into the DnCNN to estimate the output residual noise. This output noise is then subtracted from the input single-average image to derive the desired denoised single-average image. Noise images in this figure are windowed to better visualize the underlying spatial pattern (20% increased brightness and 20% decreased contrast). (D) Cross-validation plot during training of the DnCNN-54 using 2304 test denoised DWI data sets (ie, not used for training). The peak signal-to-noise ratio leveled off at about 10 epochs.

Open in a new tab

(A) The data set of 23 040 input and output images used for training and testing the proposed denoising convolutional neural network (DnCNN) comprises 10 reference eight-average diffusion-weighted image (DWI) data sets (12 sections, 12 directions [Dir], b = 50, and b = 500) and 2304 complex noise input-output pairs. Complex noise images were acquired using the same diffusion-tensor MRI (DT-MRI) sequence but with radiofrequency excitation turned off. (B) Architecture of the proposed residual deep learning DnCNN consisting of a series of 56 layers of convolution (Conv), batch normalization (Batch Norm), and rectified linear unit (ReLU) operations. Stride and padding parameters were set to [1 1] and [1 1 1 1], respectively. The purpose of the DnCNN is to estimate the residual error (or unwanted noise) from a noisy signal by employing convolutional layers and subsequently using Batch Norm for fast and stable training that may arise from ill-poised initialization and changes in distributions of internal nonlinearity. The resulting output residual image in the denoising context is the “noise image,” which can be removed subsequently by simple subtraction. Thus, for this application of the DnCNN to in vivo cardiac DT-MRI, the input of the DnCNN is acquired single-average (signal + noise) DWIs, and the output results in estimated noise images. (C) Representative example of showing a single average raw DWI b = 50 image being denoised with a comparison with a reference eight-average DWI. First, the input single-average data are fed into the DnCNN to estimate the output residual noise. This output noise is then subtracted from the input single-average image to derive the desired denoised single-average image. Noise images in this figure are windowed to better visualize the underlying spatial pattern (20% increased brightness and 20% decreased contrast). (D) Cross-validation plot during training of the DnCNN-54 using 2304 test denoised DWI data sets (ie, not used for training). The peak signal-to-noise ratio leveled off at about 10 epochs.

Quantification of the SNR and SSIM.— SNR maps were created from the 2304 noise images for each participant group by normalizing their corresponding 8Av, b = 50 diffusion-weighted image with the standard deviation of the noise images at each voxel. Furthermore, the structural similarity index (SSIM) maps were generated and compared with the 8Av reference data by calculating the local means (μx, μy), standard deviations (σx, σy, σxy), and cross-covariances (C1, C2) of the comparison image on the basis of the following equation (27):

graphic file with name ryct.2021200580.eq4.jpg

Reported estimates of the SNR and SSIM for each participant were calculated from the whole left ventricular myocardium by using a mask.

Quantification of cardiac DT-MRI parameters.— Cardiac DT-MRI parameters, including MD, FA, and HAT, were compared between 8Av, 4Av, 2Av, and 1Av DT-MRI data without and with the application of the DnCNN (4AvDCNN, 2AvDCNN, and 1AvDCNN) (23,28–30). These parameters were calculated by using open source diffusion MRI processing software in Python (DIPY; www.dipy.org) (31), and global values were determined from the entire left ventricle.

Statistical Analysis

Statistical analysis was performed to identify significant differences and similarities between 8Av, 4Av, 2Av, and 1Av DT-MRI data and 4AvDCNN, 2AvDCNN, and 1AvDCNN DT-MRI data. Biases were reported with the 95% CIs (median bias [95% CI]; P value). To validate agreement, intraclass correlation coefficient (ICC) and Bland-Altman analyses were performed, with biases and outliers reported with 95% limits of agreement (LoA). Wilcoxon signed-rank test was performed to determine differences at a significance level of P less than .05.

Results

Participant Characteristics

Among participants in the test data set (n = 10 without obesity and n = 6 with obesity), participants with obesity had a higher BMI than participants without obesity (25.6 kg/m2± 3.1 vs 47.1kg/m2 ± 14.5; P = .001); age (28 years ± 3 vs 48 years ± 11; P = .07) and sex distributions (P = .20) were not different between the two groups.

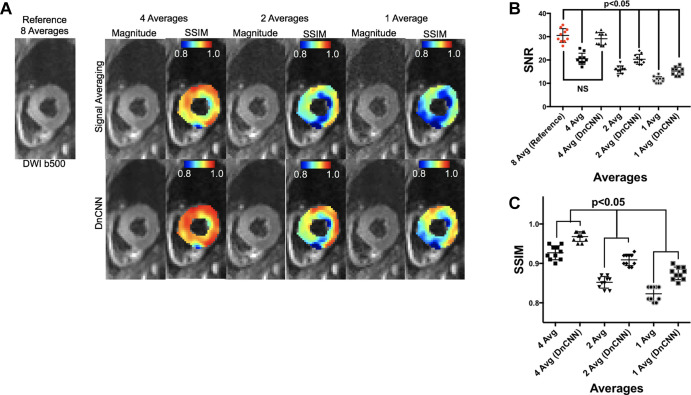
SNR and SSIM quantification.— SSIM maps for DnCNN DT-MRI data demonstrated improved homogeneity and higher SSIM values across all averages (Fig 2A). The SNR of the DnCNN DT-MRI data was increased compared with that of standard DT-MRI data (29.1 ± 2.7 [4AvDnCNN] vs 20.5 ± 2.4 [4Av]; 20.3 ± 2.1 [2AvDnCNN] vs 15.8 ± 1.7 [2Av]; and 15.2 ± 1.7 [1AvDnCNN] vs 11.5 ± 1.4 [1Av]; P < .001 for comparisons; Fig 2B). The 4AvDnCNN DT-MRI data demonstrated no difference in the SNR compared with the reference 8Av data (30.5 ± 2.9, P = .37). However, 2AvDCNN and 1AvDCNN DT-MRI data and 4Av, 2Av, and 1Av DT-MRI data showed decreased SNRs compared with 8Av reference data (P < .001). The SSIMs of the DnCNN DT-MRI data were higher than those of conventional DT-MRI data (0.968 ± 0.01 [4AvDNCC] vs 0.927 ± 0.02 [4Av]; 0.909 ± 0.01 [2AvDnCNN] vs 0.852 ± 0.01 [2Av]; and 0.875 ± 0.02 [1AvDnCNN] vs 0.823 ± 0.02 [1Av]; P < .001 for all; Fig 2C).

Figure 2:

(A) Representative magnitude and structural similarity index (SSIM) masked images at four average(s) (Avg), two averages, and one average with and without the application of the denoising convolutional neural network (DnCNN) compared with the reference eight-average diffusion-weighted b = 500 image. Note that magnitude images were windowed to better visualize the underlying spatial pattern of noise (40% increased brightness and 20% decreased contrast). (B) The signal-to-noise ratio (SNR) is not different between four-average DnCNN data and the reference eight-average data (29.1 ± 2.7 vs 30.5 ± 2.9, respectively; P = .37). SNR is different for all other comparisons (P < .001). (C) SSIM is higher after DnCNN is applied for four- two-, and one-average data (P < .001).

Open in a new tab

(A) Representative magnitude and structural similarity index (SSIM) masked images at four average(s) (Avg), two averages, and one average with and without the application of the denoising convolutional neural network (DnCNN) compared with the reference eight-average diffusion-weighted b = 500 image. Note that magnitude images were windowed to better visualize the underlying spatial pattern of noise (40% increased brightness and 20% decreased contrast). (B) The signal-to-noise ratio (SNR) is not different between four-average DnCNN data and the reference eight-average data (29.1 ± 2.7 vs 30.5 ± 2.9, respectively; P = .37). SNR is different for all other comparisons (P < .001). (C) SSIM is higher after DnCNN is applied for four- two-, and one-average data (P < .001).

Cardiac DT-MRI Parameter Quantification

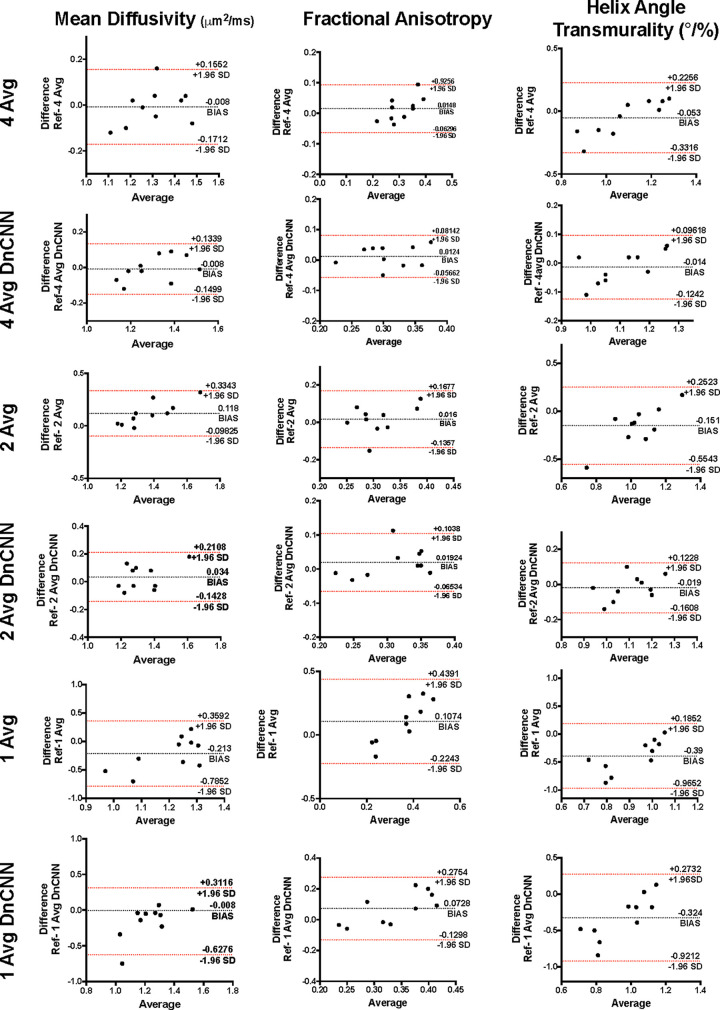
MD quantification.— The MD (Fig 5) data from 8Av DT-MRI were comparable with those of 4AvDnCNN (–0.015 [95% CI: –0.09, 0.08]; P = .73), 2AvDnCNN (0.025 [95% CI: –0.06, 0.13]; P = .26), and 4Av (0.005 [95% CI: –0.1, 0.04]; P = .76) (Table, Fig 3A). The MD data from 4AvDnCNN DT-MRI showed a stronger correlation with the MD data from reference 8Av DT-MRI than with the MD data from DT-MRI without DnCNN application (ICC, 0.863; P = .001 [with DnCNN] and ICC, 0.804; P = .004 [without DnCNN]) (Fig 3B), with only a small negative bias being shown (0.008 μm2/msec [95% LoA: –0.150, 0.134] and 0.008 μm2/msec [95% LoA: –0.171, 0.155], respectively) according to the Bland-Altman plot (Fig 4).

Figure 5:

(A) Representative diffusion-tensor MRI (DT-MRI) parameter maps (mean diffusivity [MD], fractional anisotropy [FA], and helix angle transmurality [HAT]) comparing four-, two-, and one-average (avg) data with reference eight-average data. (B) Representative DT-MRI parameter maps (MD, FA, HA) comparing DnCNN-denoised four-, two-, and one-average data with the reference eight-average data.

Open in a new tab

(A) Representative diffusion-tensor MRI (DT-MRI) parameter maps (mean diffusivity [MD], fractional anisotropy [FA], and helix angle transmurality [HAT]) comparing four-, two-, and one-average (avg) data with reference eight-average data. (B) Representative DT-MRI parameter maps (MD, FA, HA) comparing DnCNN-denoised four-, two-, and one-average data with the reference eight-average data.

Parameter Quantification of Study Participants

graphic file with name ryct.2021200580.tbl1.jpg

Open in a new tab

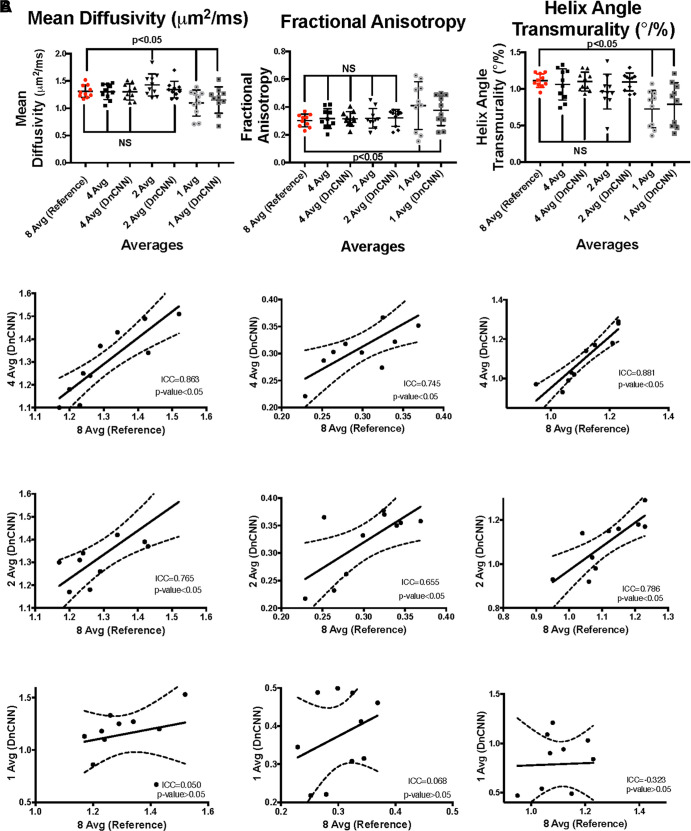
Figure 3:

(A) Comparison of the diffusion-tensor MRI (DT-MRI) parameters shows that the mean diffusivity (MD), fractional anisotropy (FA), and helix angle transmurality (HAT) have nonsignificant (NS) mean differences for four- and two-average (Avg) DT-MRI parameters with DnCNN denoising and without denoising compared with eight-average data, whereas the one-average data are significantly reduced with and without the application of the DnCNN for both MD and HAT and are increased for FA. (B) The interclass correlation plots show significant agreement between the reference eight-average data and four-average DT-MRI data with and without the application of the DnCNN, but significant agreement is not shown for two-average data, and no agreement is shown between the reference data and one-average data with or without the application of the DnCNN. DnCNN = denoising convolutional neural network, ICC = intraclass correlation coefficient.

Open in a new tab

(A) Comparison of the diffusion-tensor MRI (DT-MRI) parameters shows that the mean diffusivity (MD), fractional anisotropy (FA), and helix angle transmurality (HAT) have nonsignificant (NS) mean differences for four- and two-average (Avg) DT-MRI parameters with DnCNN denoising and without denoising compared with eight-average data, whereas the one-average data are significantly reduced with and without the application of the DnCNN for both MD and HAT and are increased for FA. (B) The interclass correlation plots show significant agreement between the reference eight-average data and four-average DT-MRI data with and without the application of the DnCNN, but significant agreement is not shown for two-average data, and no agreement is shown between the reference data and one-average data with or without the application of the DnCNN. DnCNN = denoising convolutional neural network, ICC = intraclass correlation coefficient.

Figure 4:

Bland-Altman plots of four-, two-, and one-average (Avg) diffusion-tensor MRI (DT-MRI) and denoising convolutional neural network (DnCNN) DT-MRI data for mean diffusivity, fractional anisotropy, and helix angle transmurality. SD = standard deviation.

Open in a new tab

Bland-Altman plots of four-, two-, and one-average (Avg) diffusion-tensor MRI (DT-MRI) and denoising convolutional neural network (DnCNN) DT-MRI data for mean diffusivity, fractional anisotropy, and helix angle transmurality. SD = standard deviation.

Although the MD data from 2Av and 2AvDnCNN DT-MRI showed a positive correlation with that data from reference 8Av DT-MRI (ICC, 0.765; P = .005 and ICC, 0.591; P = .001, respectively) (Fig 4B) and resulted in positive biases of 0.034 μm2/msec (95% LoA: –0.143, 0.211) and 0.118 μm2/msec (95% LoA: –0.098, 0.334), respectively (Fig 4), the conventional 2Av DT-MRI did result in a significantly increased MD (Table). The MD data from both the 1Av and 1AvDnCNN DT-MRI showed no correlation with the MD data from reference 8Av DT-MRI (ICC, 0.050; P = .49 and ICC, –0.380; P = .44 respectively) (Fig 3B).

FA quantification.— For FA (Fig 5), the 8Av DT-MRI data were not different from the 4Av (0.017 [95% CI: –0.026, 0.046]; P = .27), 4AvDnCNN (0.019 [95% CI: –0.018, 0.042]; P = .29), 2Av (0.027 [95% CI: –0.034, 0.08]; P = .30), or 2AvDnCNN (0.01 [95% CI: –0.017, 0.053]; P = .19) DT-MRI data (Table, Fig 3A).

The FA data from both 4Av and 4AvDnCNN DT-MRI correlated with that from reference 8Av DT-MRI (ICC, 0.745; P = .01 and ICC, 0.771; P = .002, respectively) (Fig 4B). Furthermore, the 4Av and 4AvDnCNN FA results showed a homoscedastic distribution and bias of 0.012 μm2/msec (95% LoA: –0.057, 0.081) and 0.015 μm2/msec (95% LoA: –0.063, 0.093), respectively, according to the Bland-Altman plots (Fig 4). The FA data from 1Av and 2Av DT-MRI showed no correlation with the FA data from reference 8Av DT-MRI (ICC, –0.051; P = .64 and ICC, 0.177; P = .65); however, the FA data from 2AvDnCNN DT-MRI data did correlate (ICC, 0.655; P = .02) (Fig 3B).

HAT quantification.— For HAT (Fig 5), the data from reference 8Av DT-MRI were not different from HAT data from 4Av (–0.015 [95% CI: –0.18, 0.08]; P = .27), 2Av (–0.125 [95% CI: –0.29, 0.02]; P = .05), 4AvDnCNN (0.005 [95% CI: –0.07 to 0.05]; P = .45), or 2AvDnCNN (–0.025 [95% CI: –0.1 to 0.06]; P = .43) (Table, Fig 3A). HAT values from the 4Av and 4AvDnCNN DT-MRI were correlated with the HAT values from reference 8Av DT-MRI (ICC, 0.881 and 0.613, respectively; P = .001 for both) (Fig 3B). The additional Bland-Altman plots revealed a homoscedastic distribution with a small negative bias of 0.014°/% (95% LoA: –0.124, 0.096) for 4Av DT-MRI and 0.053°/% (95% LoA: –0.332, 0.226) for 4AvDnCNN DT-MRI (Fig 4). The HAT values from the 1Av and 2Av DT-MRI data showed only poor correlation with the reference 8Av DT-MRI data (ICC, –0.588; P = .43 and ICC, 0.183; P = .12, respectively); the 2AvDnCNN DT-MRI data did correlate with the 8Av DT-MRI data (ICC, 0.786; P = .005), with a small bias of –0.019°/% (–0.161, 0.123) being shown (Figs 3B–4).

DT-MRI difference between the groups with and without obesity.— A comparison of the DT-MRI parameters from the reference 8Av DT-MRI between the participants in the groups with and without obesity is shown in Table and Figure 6. Compared with the group without obesity, the group with obesity had a higher MD (1.31 ± 0.11 vs 1.75 ± 0.36; P = .04), lower FA (0.3 ± 0.04 vs 0.25 ± 0.04; P = .04), and lower HAT (1.11 ± 0.09 vs 0.97 ± 0.1; P = .02). These differences in the MD, FA, and HAT between the groups with and without obesity were conserved and found to be significant for 2AvDnCNN and 4AvDnCNN DT-MRI but were not conserved or found to be significant for 2Av or 4Av DT-MRI. For both 1Av and 1AvDnCNN DT-MRI, differences between the two groups were conserved for MD and HAT but were not found to be conserved for FA.

Figure 6:

(A) Representative diffusion-tensor MRI (DT-MRI) parameter maps (mean diffusivity [MD], fractional anisotropy [FA], and helix angle [HA]) from a participant within the group with obesity comparing denoised (denoising convolutional neural network [DnCNN]) four- and two-average (avg) data with the reference eight-average data. The four-average data without denoising are shown to demonstrate an effect on the parameter quantification. (B) Significant differences are found for MD, FA, and HA transmurality between participants in the groups with and without obesity for reference eight-average data and DnCNN-denoised four- and two-average data. Conventional four-average data without the application of the DnCNN yield nonsignificant (NS) differences, which is also the case for two-average data without the application of the DnCNN. For one-average data without and with the application of the DnCNN, differences are conserved between groups with and without obesity for MD and HA transmurality but are not conserved for FA. * indicates statistical significance P < .05.

Open in a new tab

(A) Representative diffusion-tensor MRI (DT-MRI) parameter maps (mean diffusivity [MD], fractional anisotropy [FA], and helix angle [HA]) from a participant within the group with obesity comparing denoised (denoising convolutional neural network [DnCNN]) four- and two-average (avg) data with the reference eight-average data. The four-average data without denoising are shown to demonstrate an effect on the parameter quantification. (B) Significant differences are found for MD, FA, and HA transmurality between participants in the groups with and without obesity for reference eight-average data and DnCNN-denoised four- and two-average data. Conventional four-average data without the application of the DnCNN yield nonsignificant (NS) differences, which is also the case for two-average data without the application of the DnCNN. For one-average data without and with the application of the DnCNN, differences are conserved between groups with and without obesity for MD and HA transmurality but are not conserved for FA. * indicates statistical significance P < .05.

Discussion

DT-MRI of the heart is an SNR-constrained technique that requires multiple signal averages to fully characterize myocardial anisotropy. The proposed application of a residual deep learning DnCNN to in vivo cardiac DT-MRI data enables a twofold reduction in scan time while faithfully preserving image quality and DT-MRI parameter quantification, even in participants with obesity. The use of 4AvDnCNN DT-MRI preserved the SNR and SSIM as well as the MD, FA, and HAT of participants in the groups with and without obesity when compared with reference 8Av DT-MRI. Significant differences in the MD, FA, and HAT between populations with and without obesity revealed by reference 8Av DT-MRI were also maintained with 4AvDnCNN and 2AvDnCNN DT-MRI. Despite preserving the aforementioned significant differences between the groups with and without obesity, 2AvDnCNN DT-MRI exhibited reduced SNR and SSIM values compared with reference 8Av DT-MRI in participants without obesity (20.3 ± 2 vs 30.5 ± 3; P < .001 [SNR] and 0.91 ± 0.01 [SSIM]). Taken together, these data demonstrated the feasibility of accelerating in vivo cardiac DT-MRI with the application of a DnCNN by reducing scan time from 20 minutes (assuming 60 beats per minute) to 10 minutes while conserving both image quality and DT-MRI parameter quantification, increasing its clinical applicability. If SNR and SSIM values are allowed to decrease by approximately 33% and approximately 5%, respectively, then DnCNN DT-MRI could be further accelerated by a fourfold decrease in the scan time from 20 minutes to 5 minutes.

There were several limitations of this study. First, there were a small number of participants, and the study was performed at a single center. The sex and age ratios between the participants within the groups with and without obesity varied substantially, which could influence the differences revealed by cardiac DT-MRI. Despite these limitations, we demonstrated that the DnCNN faithfully preserves differences found between groups with and without obesity in half the scan time. This will allow us to more easily scan patients with obesity who have additional conditions, such as a chronic myocardial conditions, given the accelerated DT-MRI acquisition (Fig E1 [supplement]). This will enable the swift collection of further data to support these findings.

Another limitation of the application of the DnCNN is that the input noise images will depend on the acquired imaging technique and scan parameters that directly affect SNR levels (eg, coil sensitivity, field strength). In this study, the DnCNN was trained on in vivo cardiac DT-MRI data, and expanding its direct application to other MRI techniques will depend on how closely the noise distribution matches with the proposed cardiac DT-MRI sequence. However, even if retraining of the DnCNN is required for another application, acquiring noise images is less challenging at a large scale than acquiring high-fidelity and pathophysiologically relevant images. Furthermore, the outputted noise image can easily be analyzed to check for failure modes, because the expected noise output should be uncorrelated and unstructured. It is also important to consider the limitation of the DnCNN in estimating possible structured noise. Because the DnCNN is trained to only recognize unstructured noise from acquired noise images, any structured noise would not be recognized by the DnCNN and would thus still be present in the image. However, this possible limitation could be overcome by training the DnCNN to additionally recognize structured noise, such as signal fallout or aliasing, if a sufficient number of training data sets could be provided. A final potential limitation is the ability to distinguish myocardial pathophysiologic conditions that are highly diffuse and present as noise, in which case there is a potential for the DnCNN to remove such diffuse features. However, in our study, participants with obesity presented with patch-like and diffuse patterns of elevated MD and decreased FA, which were conserved by both twofold-accelerated (4AvDnCNN) and fourfold-accelerated (2AvDnCNN) DnCNN DT-MRI. Further studies will be needed to determine the feasibility of DnCNN DT-MRI detecting cardiomyopathies with more diffuse presentations, such as hypertrophic and dilated variations.

We demonstrated that applying a DnCNN to in vivo cardiac DT-MRI data can result in a twofold scan acceleration while preserving both image quality and DT-MRI parameter quantification. DnCNN DT-MRI could potentially be used to further accelerate in vivo cardiac DT-MRI by a factor of four, while maintaining accurate DT-MRI parameters if image quality can be reduced. Furthermore, the accelerated DnCNN DT-MRI technique conserved the ability to detect microstructural differences between groups of participants with and without obesity when compared with the conventional DT-MRI technique.

Acknowledgments

Acknowledgment

We would like to acknowledge Jaume Coll-Font, PhD, for his contributions regarding signal processing theory.

Supported by the National Institutes of Health (grants R01 HL135242, R01 HL151704, R01 HL131635, and R01 HL141563).

Disclosures of Conflicts of Interest: K.P. disclosed no relevant relationships. M.v.d.B. disclosed no relevant relationships. R.E. disclosed no relevant relationships. S.A.M. disclosed no relevant relationships. A.S. disclosed no relevant relationships. J.K. disclosed no relevant relationships. S.P. disclosed no relevant relationships. T.G.R. disclosed no relevant relationships. C.M. disclosed no relevant relationships. S.D. Activities related to the present article: author’s institution has research funding from the American Heart Association (AHA). Activities not related to the present article: disclosed no relevant relationships. Other relationships: disclosed no relevant relationships. D.G. Activities related to the present article: disclosed no relevant relationships. Activities not related to the present article: author is on medical advisory boards for New View Surgical and Boston Scientific; author received consultancy fees from Ethicon, Medtronic, and Boston Scientific. Other relationships: disclosed no relevant relationships. R.S. Activities related to the present article: disclosed no relevant relationships. Activities not related to the present article: author received consultancy fees from Myokardia, Best Doctors, and Amgen; author’s spouse works at Wolters Kluwer UpToDate; author’s institution has grants/grants pending from AHA and National Institutes of Health (NIH); author has patents for exRNA signatures of cardiac remodeling; author has Pfizer stock and had Gilead stock, which has been sold. Other relationships: disclosed no relevant relationships. D.E.S. Activities related to the present article: author has grant from NIH. Activities not related to the present article author has grants/grants pending from NIH; author’s institution has patents with Mass General Brigham, with no money received. Other relationships: disclosed no relevant relationships. C.N. Activities related to the present article: author’s institution has grant from NIH. Activities not related to the present article: disclosed no relevant relationships. Other relationships: disclosed no relevant relationships.

Abbreviations:

Av
average
AvDnCNN
Av with application of the DnCNN
BMI
body mass index
CNN
convolutional neural network
DnCNN
denoising CNN
DT-MRI
diffusion-tensor MRI
FA
fractional anisotropy
HA
helix angle
HAT
HA transmurality
ICC
intraclass correlation coefficient
LoA
limits of agreement
MD
mean diffusivity
PSNR
peak SNR
SNR
signal-to-noise ratio
SSIM
structural similarity index

References

  • 1.Kenchaiah S, Evans JC, Levy D, et al. Obesity and the risk of heart failure. N Engl J Med 2002; 347(5):305–313. [DOI] [PubMed] [Google Scholar]
  • 2.Wong CX, Abed HS, Molaee P, et al. Pericardial fat is associated with atrial fibrillation severity and ablation outcome. J Am Coll Cardiol 2011; 57(17):1745–1751. [DOI] [PubMed] [Google Scholar]
  • 3.Pascual M, Pascual DA, Soria F, et al. Effects of isolated obesity on systolic and diastolic left ventricular function. Heart 2003; 89(10):1152–1156. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 4.Khan JN, Wilmot EG, Leggate M, et al. Subclinical diastolic dysfunction in young adults with type 2 diabetes mellitus: a multiparametric contrast-enhanced cardiovascular magnetic resonance pilot study assessing potential mechanisms. Eur Heart J Cardiovasc Imaging 2014; 15(11):1263–1269. [DOI] [PubMed] [Google Scholar]
  • 5.Shah RV, Abbasi SA, Neilan TG, et al. Myocardial tissue remodeling in adolescent obesity. J Am Heart Assoc 2013; 2(4):e000279. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 6.Kucukseymen S, Neisius U, Rodriguez J, Tsao CW, Nezafat R. Negative synergism of diabetes mellitus and obesity in patients with heart failure with preserved ejection fraction: a cardiovascular magnetic resonance study. Int J Cardiovasc Imaging 2020; 36(10):2027–2038. [DOI] [PubMed] [Google Scholar]
  • 7.Mekkaoui C, Jackowski MP, Kostis WJ, et al. Myocardial scar delineation using diffusion tensor magnetic resonance tractography. J Am Heart Assoc 2018; 7(3):e007834. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 8.Nielles-Vallespin S, Khalique Z, Ferreira PF, et al. Assessment of myocardial microstructural dynamics by in vivo diffusion tensor cardiac magnetic resonance. J Am Coll Cardiol 2017; 69(6):661–676. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 9.Ariga R, Tunnicliffe EM, Manohar SG, et al. Identification of myocardial disarray in patients with hypertrophic cardiomyopathy and ventricular arrhythmias. J Am Coll Cardiol 2019; 73(20):2493–2502. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 10.Nguyen CT, Dawkins J, Bi X, Marbán E, Li D. Diffusion Tensor cardiac magnetic resonance reveals exosomes from cardiosphere-derived cells preserve myocardial fiber architecture after myocardial infarction. JACC Basic Transl Sci 2018; 3(1):97–109. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 11.Sosnovik DE, Mekkaoui C, Huang S, et al. Microstructural impact of ischemia and bone marrow-derived cell therapy revealed with diffusion tensor magnetic resonance imaging tractography of the heart in vivo. Circulation 2014; 129(17):1731–1741. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 12.Le Bihan D, Poupon C, Amadon A, Lethimonnier F. Artifacts and pitfalls in diffusion MRI. J Magn Reson Imaging 2006; 24(3):478–488. [DOI] [PubMed] [Google Scholar]
  • 13.Lam F, Babacan SD, Haldar JP, Weiner MW, Schuff N, Liang ZP. Denoising diffusion-weighted magnitude MR images using rank and edge constraints. Magn Reson Med 2014; 71(3):1272–1284. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 14.McGraw T, Vemuri BC, Chen Y, Rao M, Mareci T. DT-MRI denoising and neuronal fiber tracking. Med Image Anal 2004; 8(2):95–111. [DOI] [PubMed] [Google Scholar]
  • 15.Veraart J, Novikov DS, Christiaens D, Ades-Aron B, Sijbers J, Fieremans E. Denoising of diffusion MRI using random matrix theory. Neuroimage 2016; 142(394):406. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 16.Manjón JV, Coupé P, Concha L, Buades A, Collins DL, Robles M. Diffusion weighted image denoising using overcomplete local PCA. PLoS One 2013; 8(9):e73021. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 17.Kofler A, Haltmeier M, Schaeffter T, et al. Neural networks-based regularization for large-scale medical image reconstruction. Phys Med Biol 2020; 65(13):135003. [DOI] [PubMed] [Google Scholar]
  • 18.Suzuki Y, Kawaji K, Patel AR, Tamura S, Hayamizu S. Toward effective noise reduction for sub-Nyquist high-frame-rate MRI techniques with deep learning. In: Proceedings of the 2017 Asia-Pacific Signal and Information Processing Association Annual Summit and Conference (APSIPA ASC). Piscataway, NJ: IEEE, 2017; 1136–1139. [Google Scholar]
  • 19.Hauptmann A, Arridge S, Lucka F, Muthurangu V, Steeden JA. Real-time cardiovascular MR with spatio-temporal artifact suppression using deep learning-proof of concept in congenital heart disease. Magn Reson Med 2019; 81(2):1143–1156. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 20.Gramfort A, Poupon C, Descoteaux M. Denoising and fast diffusion imaging with physically constrained sparse dictionary learning. Med Image Anal 2014; 18(1):36–49. [DOI] [PubMed] [Google Scholar]
  • 21.Tian Q, Bilgic B, Fan Q, et al. DeepDTI: high-fidelity six-direction diffusion tensor imaging using deep learning. Neuroimage 2020; 219117017. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 22.Zhang K, Zuo W, Chen Y, Meng D, Zhang L. Beyond a Gaussian denoiser: residual learning of deep CNN for image denoising. IEEE Trans Image Process 2017; 26(7):3142–3155. [DOI] [PubMed] [Google Scholar]
  • 23.Nguyen C, Fan Z, Xie Y, et al. In vivo diffusion-tensor MRI of the human heart on a 3 Tesla clinical scanner: an optimized second order (M2) motion compensated diffusion-preparation approach. Magn Reson Med 2016; 76(5):1354–1363. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 24.Stoeck CT, von Deuster C, Genet M, Atkinson D, Kozerke S. Second-order motion-compensated spin echo diffusion tensor imaging of the human heart. Magn Reson Med 2016; 75(4):1669–1676. [DOI] [PubMed] [Google Scholar]
  • 25.Nguyen C, Fan Z, Sharif B, et al. In vivo three-dimensional high resolution cardiac diffusion-weighted MRI: a motion compensated diffusion-prepared balanced steady-state free precession approach. Magn Reson Med 2014; 72(5):1257–1267. [DOI] [PubMed] [Google Scholar]
  • 26.Nguyen CT, Christodoulou AG, Coll-Font J, et al. Free-breathing diffusion tensor MRI of the whole left ventricle using second-order motion compensation and multitasking respiratory motion correction. Magn Reson Med 2021; 85(5):2634–2648. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 27.Wang Z, Bovik AC, Sheikh HR, Simoncelli EP. Image quality assessment: from error visibility to structural similarity. IEEE Trans Image Process 2004; 13(4):600–612. [DOI] [PubMed] [Google Scholar]
  • 28.Scott AD, Nielles-Vallespin S, Ferreira PF, McGill LA, Pennell DJ, Firmin DN. The effects of noise in cardiac diffusion tensor imaging and the benefits of averaging complex data. NMR Biomed 2016; 29(5):588–599. [DOI] [PubMed] [Google Scholar]
  • 29.Scott AD, Ferreira P, Nielles-Vallespin S, et al. Improved in-vivo cardiac DTI using optimal b-values. J Cardiovasc Magn Reson 2014; 16(Supplement 1):O27. [Google Scholar]
  • 30.Ma S, Nguyen CT, Christodoulou AG, et al. Accelerated cardiac diffusion tensor imaging using joint low-rank and sparsity constraints. IEEE Trans Biomed Eng 2018; 65(10):2219–2230. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 31.Garyfallidis E, Brett M, Amirbekian B, et al. DIPY—a novel software library for diffusion MR and tractography. In: Proceedings of the 17th Annual Meeting of the Organization for Human Brain Mapping.Minneapolis, Minn: Organization for Human Brain Mapping, 2011; 1–5. [Google Scholar]

Articles from Radiology: Cardiothoracic Imaging are provided here courtesy of Radiological Society of North America

RESOURCES