Abstract
Tomographic imaging via penetrating waves generates cross-sectional views of the internal anatomy of a living subject. For artefact-free volumetric imaging, projection views from a large number of angular positions are required. Here, we show that a deep-learning model trained to map projection radiographs of a patient to the corresponding 3D anatomy can subsequently generate volumetric tomographic X-ray images of the patient from a single projection view. We demonstrate the feasibility of the approach with upper-abdomen, lung, and head-and-neck computed tomography scans from three patients. Volumetric reconstruction via deep learning could be useful in image-guided interventional procedures such as radiation therapy and needle biopsy, and might help simplify the hardware of tomographic imaging systems.
The ability of computed tomography (CT) to take a deep and quantitative look of a patient or an object with high spatial resolution holds significant value in scientific explorations and in medical practice. Traditionally, a tomographic image is obtained via the mathematical inversion of the encoding function of the imaging wave for a given set of measured data from different angular positions (Figs. 1a,b). A prerequisite for artefact-free inversion is the satisfaction of the classical Shannon-Nyquist theorem in angular-data sampling, which imposes a practically achievable limit in imaging time and object irradiation. To mitigate the problem, image reconstruction with sparse sampling has been investigated extensively via techniques such as compressed-sensing1–6 and maximum a posteriori7,8. This type of approaches introduces a regularization term to the inversion to encourage some ad hoc or presumed characteristics in the resultant image9–13. If imaging quality cannot be compromised, the resultant sparsity is generally limited and does not address the unmet demand for real-time imaging with substantially reduced subject irradiation (Fig. 1c). Indeed, while continuous efforts have been made to reduce the number of angular measurements in medical imaging, tomographic imaging with ultra-sparse sampling has yet to be realized.
Fig. 1 |. 3D image reconstruction with ultra-sparse projection-view data.
a, A geometric view of an X-ray source, a patient and a detector in a CT system. b, X-ray projection views of a patient from three different angles. c, Different image-reconstruction schemes in the context of prior knowledge and projection sampling. d, Volumetric image reconstruction using deep learning with one or multiple 2D projection images.
In this work, we push sparse sampling to the limit of a single projection view, and demonstrate single-view tomographic imaging with a patient-specific prior by leveraging deep learning and the seamless integration of prior knowledge in the data-driven image-reconstruction process. The harnessing of prior knowledge by machine-learning techniques in different data domains for improved imaging is an emerging topic of research. Some recent studies14–19 have also investigated machine-learning-based image reconstruction. Whereas the data-driven approach represents a potentially general strategy for image reconstruction, here single-view CT imaging is achieved via a patient-specific prior. Practically, it is actually advantageous to work with the patient-specific prior: for many image-guided interventional applications, the approach would enable scenarios most relevant to the specific patient under treatment.
Deep neural networks have attracted much attention for their ability to learn complex relationships and to incorporate existing knowledge into the inference model through feature extraction and representation learning20–22. The method has found widespread applications across disciplines, such as computer vision23–25, autonomous driving26, natural language processing27, and biomedicine15,28–36. Here, we design a hierarchical neural network for X-ray CT imaging with ultra-sparse projection views, and develop a structured training process for deep learning to generate three-dimensional (3D) CT images from two-dimensional (2D) X-ray projections. Our approach introduces a feature-space transformation between a 2D projection and a 3D volumetric CT image within a representation–generation (encoder–decoder) framework. By using the transformation module, we transfer the representations learned from the 2D projection into a representative tensor for 3D volume reconstruction in the subsequent generation network. Through the model-training process, the transformation module learns the underlying relationship between feature representations across dimensionality, making it possible to generate a volumetric CT image from a 2D projection. It should be emphasized that an X-ray projection is not a purely 2D cross-sectional image, as higher dimensional information is already encoded during the projection process (see schematic in Fig. 1a), with the encoding function determined by the physics of interactions between the X-ray and media. Generally, a single projection alone is not sufficient for capturing the anatomical information in the projection direction for the subsequent volumetric-image reconstruction. What enables our deep-learning model for patient-specific volumetric image reconstruction is that anatomical relations (including the information in the direction of the projection view) are encoded during the model-training process via the use of augmented datasets containing different 2D–3D data pairs of body positions and anatomical distributions. The deep-learning transformation deciphers the hidden information in the projection data, and predicts a volumetric image with the help of prior knowledge gained during model training (Fig. 1d).
Results
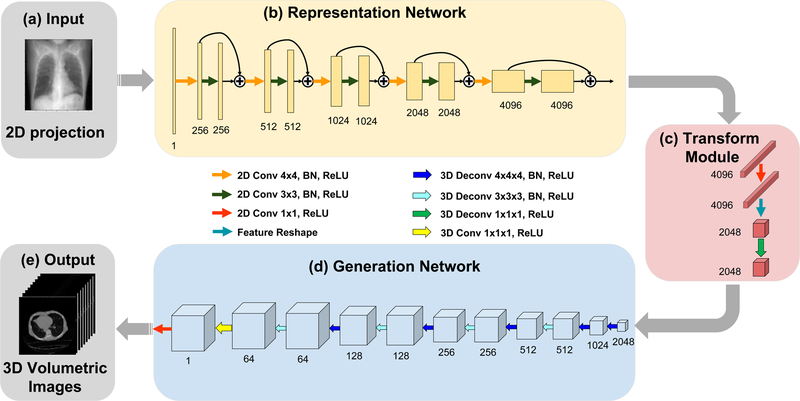
Figure 2 shows the detailed structure of our deep-learning framework. The input to the neural network is a single or multiple 2D projection images from different view angles. The output of the network is the corresponding volumetric CT image. During the model-training process, the neural network learns the mapping function from the 2D projection(s) to the volumetric image. Specifically, our deep-learning architecture consists of three main parts: a representation network, a transformation module, and a generation network. The representation network extracts embedding features and learns a semantic representation of the actual 3D scene from the input 2D projection(s). The transformation module bridges the representation and generation networks through convolution and deconvolution operations and relates the 2D and 3D feature representations. The role of the generation network is to provide volumetric images with subtle structures based on the learned features from the representation network. In constructing the model, we assume that one or more 2D projections and the corresponding 3D image possess the same semantic representation, as they represent the same object or scene. In other words, the representation in feature space remains invariant in the transformation of a 2D projection into a 3D image. To a large extent, the task of 3D image reconstruction here is to train the encoder (that is, the representation network) and decoder (that is, the generation network) to learn reliably the relationship between the feature space and image space. Details about the network architecture are included in Methods.
Fig. 2 |. Architecture of the deep-learning network.
a, The input of the model is a single projection view or multiple 2D projection views. b, The representation network learns the feature representation of the imaged object from the input. c, The extracted 2D features are reshaped and transferred by the transformation module to a 3D representation, for subsequent reconstruction. d, The generation network uses representation features extracted in the former stages to generate the corresponding volumetric images. e, The output of the model is a set of volumetric images. Notation: “Conv”: convolution layer; “Deconv”: deconvolution layer; (the numbers indicate the specific kernel size used); “BN”: batch normalization; “ReLU”: rectified linear unit; “+”: indicates feature-map addition with residual path; the numbers underneath each layer denote the number of feature maps for each layer.
Training a deep-learning model requires a large number of annotated data, and this is often a bottleneck37. Instead of actually measuring a large number of paired X-ray projections and CT images for supervised training, we digitally produce projection images from a CT image of a patient by using the geometry consistent with a clinical on-board cone-beam CT system for radiation therapy (Fig. 1a). For imaging in the thoracic or upper abdominal region, where four-dimensional (4D) CT is often acquired to resolve organ motion caused by involuntary respiration, each 4D phase (that is, phase-resolved) CT is selected to form a 3D-CT dataset. In reality, a 3D CT image captures only one out of numerous possible scenarios of the patient’s internal anatomy. To consider various clinical situations in the modeling, a series of translations, rotations and organ deformations are introduced to the 3D-CT to mimic different imaging situations. For each of the transformations, the corresponding 2D projection image or digitally reconstructed radiograph (DRR) for one or more specified angles is produced. In this way, a dataset of DRR-CT pairs is generated for the training and testing of the deep-learning model. In practice, the dataset produced by using the CT of a given patient can be employed to train a patient-specific deep-learning model for subsequent volumetric imaging of the same patient. The model can be used for interventional procedures, such as radiation therapy and image-guided biopsy, where pre-operational CT can be employed to train the deep-learning model. One may, of course, construct a training dataset composed of an ensemble of patients with the above-mentioned DRR-CT pairs. This would lead to a more generally applicable model, yet the fundamental principle would be the same. For simplicity, we will focus on the development of a patient-specific 2D–3D image mapping model.
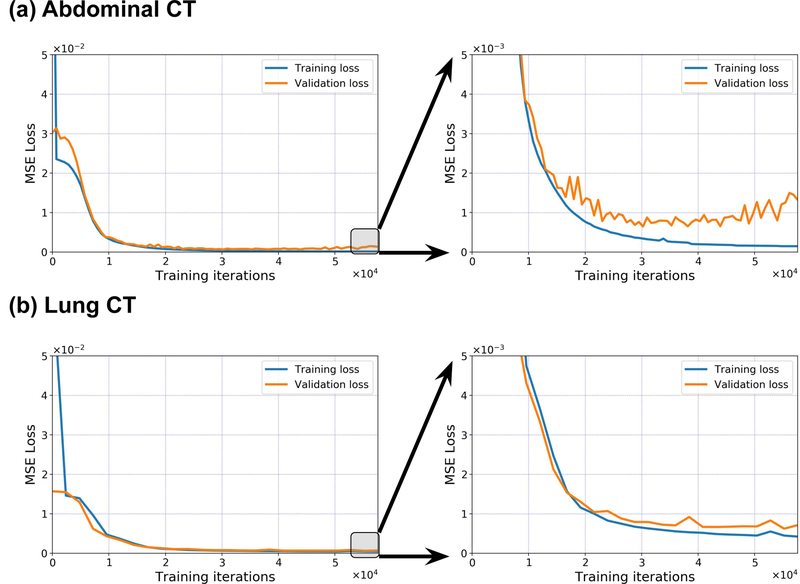
We evaluate the approach by using different disease sites: an upper-abdominal case, a lung case, and a head-and-neck case. We use the anterior-posterior (AP) 2D projection as input (Fig. 2). In all experiments, the same network architecture and training strategy are used. The loss curves (Fig. 3) indicate that the model is trained to fit the training data well, and can also generalize to work on the data not included in the training datasets. The details of dataset generation and training process are described in Methods.
Fig. 3 |. Training-loss and validation-loss curves of the image reconstruction with a single projection view, for the abdominal-CT and lung-CT cases.
MSE, mean squared error.
To evaluate the feasibility of the approach, we deploy the trained network on an independent testing dataset. Fig. 4a shows our reconstruction results with a single AP-view input for the abdominal-CT and lung-CT cases, together with the ground-truth CT images and the difference images between the obtained images and the ground truth. The deep-learning-derived images resemble the target images, indicating the potential of the model for volumetric imaging. We also reconstruct volumetric images with a single lateral view as input for the abdominal case, with similar results (see the Experiments section of the Supplementary Information). Furthermore, we use multiple quantitative evaluation metrics to measure the results. Table 1 summarizes the average values of the evaluation metrics. The qualitative and quantitative results demonstrate that our model is capable of achieving 3D image reconstruction even with only a single 2D projection. The results (Fig. 5) also confirm the validity of our approach.
Fig. 4 |. Examples from the abdominal-CT and lung-CT cases.
Different numbers of 2D projections are used for the prediction. a–d, Images reconstructed by using 1, 2, 5, and 10 projection views. The corresponding coronal and sagittal views of the images for both experiments are presented in Supplementary Figs. 3–6. For the abdominal-CT case, 720, 180, and 600 images are used for training, validation and testing, respectively. For the lung-CT case, 2400, 600, and 200 images are used for training, validation and testing, respectively.
Table 1 |.
Reconstruction results for the abdominal-CT and lung-CT cases.
| Number of 2D Projections | Abdominal CT | Lung CT | ||||||
|---|---|---|---|---|---|---|---|---|
| MAE | RMSE | SSIM | PSNR | MAE | RMSE | SSIM | PSNR | |
| 1 | 0.018 | 0.177 | 0.929 | 30.523 | 0.025 | 0.385 | 0.838 | 27.157 |
| 2 | 0.015 | 0.140 | 0.945 | 32.554 | 0.024 | 0.399 | 0.837 | 26.985 |
| 5 | 0.016 | 0.155 | 0.942 | 31.823 | 0.028 | 0.452 | 0.831 | 26.247 |
| 10 | 0.018 | 0.165 | 0.939 | 31.355 | 0.027 | 0.429 | 0.817 | 26.636 |
MAE, mean absolute error; RMSE, root mean squared error; SSIM, structural similarity; PSNR, peak signal noise ratio.
Fig. 5 |. Examples from the head-and-neck-CT case.
a, 3D CT images of a head-and-neck case used for the training of the deep-learning model. b, Left, Testing samples and the corresponding difference images (with respect to the training samples) in the transverse, sagittal and coronal planes. Right, Predicted images and the corresponding difference images (with respect to the ground truth) in the transverse, sagittal and coronal planes. For this case, 2000, 500 and 200 images are used for training, validation and testing, respectively.
In addition, we conduct experiments with 2, 5 and 10 projection views as inputs. The multiple-view angles are distributed evenly around a 180-degree semicircle (for instance, for 2 views, the two orthogonal directions are 0- (AP) and 90-degree (lateral)). We stack the 2D projections from different view angles as of the input data and modify the first convolution layer to fit the input channel size. With the same model-training procedure and hyper-parameters, we obtain the CT images for 2, 5 and 10 views for both the abdominal-CT and lung-CT cases (Figs. 4b–d). The quantitative evaluation of the results for these cases is summarized in Table 1. The training-loss curves and the corresponding coronal and sagittal views of the images are shown in Supplementary Figs. 1–2 and Figs. 3–6, respectively. By comparing the quantitative evaluation metrics, it is clear that a single 2D projection is capable of producing a reconstructed image similar to that obtained with multiple projections. In a sense, the network structure is optimized for a single-view input. Generally, there should be an interplay between the number of projections and the architecture of the hierarchical network in deep-learning-based reconstruction. More projections should either lead to better performance or yield room to simplify the network structure because the learned representation is generally enhanced with the additional projection information.
Fig. 6 |. Analysis of feature maps.
a, Visualization of the feature maps, learned from different 2D projections, for two testing samples. The different colors in the figure indicate different intensity values in the feature maps (a lighter color indicates a higher intensity value). b, T-SNE visualization of the feature representations of 15 testing examples with the input of different 2D views. A total of 15 clusters (4 points of the same color) are shown. The 4 points in a cluster represent the learned features from 1-, 2-, 5-, and 10-view reconstruction models. Each cluster denotes the embedded representations for each of the 15 randomly chosen testing samples. c, Correlation matrix of representation vectors in 1-view and 2-view reconstructions from 50 randomly chosen testing samples out of 600.
Discussion
To better understand the deep-learning model, we analyze the semantic representations learned from the model. Generally speaking, successful generation of volumetric images is possible only if the model is able to learn the semantic representation of the 3D structure from the input projections. Hence, for the same volume, the representations obtained via learning from different angular projections should be similar, since they describe the same underlying 3D scene. In Fig. 6a, we visualize the feature maps extracted from the transformation module for two testing samples. For visualization purposes, only 5 randomly chosen channels among the 4096 feature maps are shown, each with a size of 4×4 pixels. The feature maps learned from different numbers of 2D projections are displayed separately in different columns. The results show that, when different 2D views are given, the model extracts similar semantic representations of the underlying 3D scene. Furthermore, Fig. 6b shows the visualization of t-Distributed Stochastic Neighbor Embedding (t-SNE) for the feature maps of 15 testing samples. The t-SNE technique is commonly used to visualize high-dimensional data by embedding each sample as a point in a 2D space38. The four points in a cluster of the same color represent the learned features from 1-, 2-, 5-, and 10-view reconstructions. The figure shows a clustering behavior for feature maps from the same sample, indicating that the model learns a similar representation from different 2D projections.
We also measure the similarity of the embedding representations by calculating the Euclidean distance between two feature maps. In this way, we compute a similarity score, ranging from 0 to 1, where high similarity (a score approaching 1) indicates that the distance between two feature maps is closer to zero. We plot a correlation matrix (Fig. 6c) among 50 randomly selected testing samples, with their feature representations extracted from 1-view and 2-view reconstruction models. The highest values stand out in the diagonal of the correlation matrix while other off-diagonal values remain relatively low. This illustrates that the two sets of feature representations learned from 1-view and 2-view projections for the same 3D scene are the most similar, or the closest in Euclidean distance space, compared to the feature representations learned from other different 3D scenes. This provides additional evidence supporting that the model is capable of learning a semantic representation of the 3D scene with a single projection.
Robustness against possible irregular breathing patterns is important for future clinical implementation of the approach. The robustness of deep networks against various perturbations is an intense area of research in artificial intelligence39–46. As summarized in ref. 43, possible solutions can belong to three categories: (i) the modification of network architectures (for example, adding more layers, changing the loss function, and modifying the activation functions); (ii) the use of external models as a network add-on to detect out-of-distribution data (for example, using an external detector to rectify the irregular data); and (iii) the modification of the training-data distribution or the training strategy (for example, adding regularization, data augmentation, or leveraging adversarial training). In (i), the efforts are focused on refining the learning models. In (ii), irregular motions might be regarded as out-of-distribution data, where some potential techniques, such as a detector subnetwork41 or the confidence-based method42,44, might be helpful for detecting irregular input. Among the various methods, the modification of the training-data distribution is arguably the most straightforward way to proceed. The rationale is that, if the irregularities can be incorporated effectively into the training dataset and the training strategy can be adjusted accordingly, the robustness of the trained model would be enhanced. To a certain extent, this has been elaborated in the example in Supplementary Fig. 7, where it is demonstrated that, because of the inclusion of augmented training datasets with rotational transformations, the deep-learning approach is much more robust against a small rotation of the imaging subject than a conventional principal component analysis (PCA)-based method. Quantitative results of the study for the testing sample illustrated in Supplementary Fig. 7 are presented in Supplementary Table 1.
Outlook
We have described a deep-learning approach for volumetric imaging with ultra-sparse data sampling and a patient-specific prior. The data-driven strategy is capable of holistically extracting the feature characteristics embedded in a single projection or in a few 2D projections, and of transforming them into the corresponding 3D image through model learning. The image-feature space transformation plays an essential role in the ultra-sparse image reconstruction. At the training stage, the method incorporates diverse forms of a priori knowledge into the reconstruction. The manifold-mapping function is learned from the training datasets, rather than relying on any ad hoc form of motion trajectory. Although we have used X-ray imaging and patient-specific data, the concept and implementation of the approach could be extended to other imaging modalities or to other data domains with ultra-sparse sampling. Practically, the single-view imaging represents a potential solution for many image-guided interventional procedures and may help to simplify the hardware of tomographic imaging systems.
Methods
Problem formulation.
We formulate the problem of 3D image reconstruction from 2D projection(s) into a deep-learning framework. Given a sequence of 2D projections denoted as , where for all and is the number of given 2D projections, the goal is to generate a volumetric 3D image describing the corresponding 3D physical scene. With the sequence of 2D projections as input, the deep-learning model outputs the predicted 3D volume denoted as , while is the ground truth 3D image as the reconstruction target. Note that network prediction is of the same size as ground truth image , where each entry is a voxel-wise intensity value. Thus, the problem is formulated as finding a mapping function transforming 2D projections to volumetric images. To tackle this problem, a deep-learning model is trained to find the mapping function , which uses 2D projections as input and predicts the corresponding 3D image , as expressed in equation (1).
| (1) |
In order to use a sequential of 2D projections as model input, we stack all the 2D projections together as a single 3D tensor. In other words, a set of 2D projections are stacked as a 3D volume , where is the number of 2D projections. In what follows, we introduce the model architecture of the deep neural network in detail.
Encoder–decoder framework.
The deep neural network is formulated into an encoder–decoder framework (Fig. 2). In the auto-encoder model47, the encoder converts high-dimensional data into embedded representations while the decoder reconstructs high-dimensional input. In our task, instead of decoding to get the input, we developed a modified decoder to generate the corresponding volumetric images based on the codes converted by the encoder. More precisely, with a sequence of 2D projections as input, the encoder network learns the feature representation by extracting semantic information from 2D projections, such as organ position and size. In this way, the encoder network learns a transformation function from the 2D image domain to the feature domain. A transformation module then follows to learn the manifold mapping function in the feature domain to transform the feature representation across dimensions. Using the learned feature representation as the input, the decoder network is trained to generate the 3D volume. In other words, the decoder network learns a transformation function from the feature domain to the 3D image domain. In this way, we fit the target mapping function by decomposition: . The rationale behind our network design is that both 2D projections and 3D images should share the same semantic feature representation in the feature domain, as they represent the image expressions of the same object or physical scene. Accordingly, the representation in feature space should remain invariant. In a sense, if the model can learn the transformation function between the feature space and the 2D/3D image space, it is possible to reconstruct 3D images from 2D projections. Therefore, following this encoder–decoder framework, our model is able to learn how to generate 3D images from 2D projections by leveraging from the learned representations in high-dimensional feature space.
Representation network.
Superb performance has been achieved by deep residual networks (such as ResNet)48 in many tasks. A key step in residual learning is the identity mapping that facilitates the training process and avoids gradient vanish in back-propagation48, which encourages residual learning of the hierarchical representation at each stage and eases the training of the deep network. Motivated by this feature, we introduce a residual-learning scheme in the representation network (Fig. 2), where the 2D convolution residual block is used to assist the deep model to learn semantic representations from 2D projections. More details about the residual learning scheme are presented in the “Ablative study and discussion” section of the Supplementary Information, and the results are summarized in Supplementary Table 2. Specifically, each 2D convolution residual block consists of a pattern of “2D convolution layer (with kernel size 4 and stride 2) → 2D batch normalization layer → rectified linear unit activation (ReLU) layer → 2D convolution layer (with kernel size 3 and stride 1) → 2D batch normalization layer → ReLU layer”. The first layer conducts 2D convolution operations using a kernel with sliding stride , which down-samples the spatial size of the feature map by a factor 2. In addition, to keep the sparsity of high-dimensional feature representation, we correspondingly doubled the channel number of the feature maps by increasing the number of convolutional filters. A distribution normalization layer among the training mini-batch (batch normalization)49 then follows before feeding the feature maps through the ReLU layer50. Next, the second 2D convolution layer and 2D batch normalization layer are done by a kernel size of and sliding stride , which keeps the spatial shape of the feature maps. Moreover, before applying the second ReLU layer, an extra shortcut path is established to add up the output of the first convolution layer to obtain the final output. By setting up the shortcut path of identity mapping, the second convolution layer is encouraged to learn the residual feature representations. In order to extract hierarchical semantic features from 2D projections, we constructed the representation network by concatenating five 2D convolution residual blocks with different number of convolutional filters. A detailed discussion of the network depth is available in the “Ablative study and discussion” section of the Supplementary Information, with some results illustrated in Supplementary Fig. 8. To be concise, we use the notation of to denote channels of feature maps in a spatial size of . In the generation network, the size of input images is denoted as , where is the number of 2D projections. The change of feature map size through the network are: , where each means going through a 2D convolution residual block as described above, except that batch normalization and ReLU activation are removed in the first convolution layer. Thus, the output of the representation network is a feature representation extracted from 2D projections with a size of .
Transformation module.
To bridge the representation and generation networks, a transformation module is deployed after learning the representations. As shown in Fig. 2, by taking the convolution operations with a kernel size of and ReLU activation, the 2D convolution layer learns a transformation across all 2D feature maps. Then, we reshape embedded representations from to . In this way, we transform the feature representation across dimensions for subsequent 3D volume generation. Next, a 3D deconvolution layer with a kernel size of and sliding stride of learns a transformation among all 3D feature cubes while keeping the feature size unchanged. This transformation module bridges the 2D and 3D feature spaces. Moreover, as described in previous work51, we also remove the batch normalization in the transformation module to help the knowledge transfer through this module.
Generation network.
The generation network was built upon the 3D deconvolution block, which consists of a pattern of “3D deconvolution layer (with kernel size 4 and stride 2) → 3D batch normalization layer → ReLU layer → 3D deconvolution layer (with kernel size 3 and stride 1) → 3D batch normalization layer → ReLU layer”. Note that the “deconvolution” layer actually means the operation of “transformed convolution” or fractional stride convolution which performs up-sampling operation. The first deconvolution layer up-samples a feature map by a factor 2 with a kernel and sliding stride . In order to transform from a high-dimensional feature domain to a 3D-image domain, we accordingly reduce the number of feature maps by decreasing the number of deconvolutional filters. The second deconvolution layer with a kernel and sliding stride keeps the spatial shape of feature maps. A 3D batch normalization layer and a ReLU layer follow after each deconvolution layer. Hierarchically, the 3D generation network consists of 5 concatenating deconvolution residual blocks. Following the same convention as in the representation network, we use a notation of to denote channels of 3D feature maps with a spatial size of . With a representation input of , the data flow of the feature maps is: , where each denotes a 3D residual block. At the end of the generation network, an output transformation module was constructed with a 3D convolution layer and a 2D convolution layer with a kernel size of , which outputs 3D images fitting the shape of the reconstructed images. Finally, the generation network outputs the predicted 3D images of size , where is the size of the target volumetric images along z-axis. Note that in the output transformation module, the batch normalization layer is removed, and that there is no ReLU layer after the final convolution layer.
Materials.
The approach is evaluated by using three cases of different disease sites. In the first study, a 10-phase upper abdominal 4D-CT scan of a patient for radiation therapy (RT) treatment planning is selected. To proceed, the first 6 phases are used to generate the CT-DRR pairs for model training and validation with the procedure described above. We use the anterior-posterior (AP) 2D projection as input (Fig. 2). With translation, rotation and deformation introduced to the CT volume, we obtain a total of 720 DRRs representing different scenarios of the patient anatomy for model training and 180 DRRs for validation. To ensure that the testing data are not seen in the model-training process, we generate 600 testing DRR samples independently from the remaining 4 phases of the 4D-CT. The 4D-CT images are acquired with 120 kV, 80 mA on a Positron emission tomography–computed tomography (PET-CT) simulator (Biograph mCT 128, Siemens Medical Solutions, Erlangen, Germany) together with a Varian Real-time Position Management™ (RPM) system (Varian Medical Systems, Palo Alto, CA). The 2D projection data are obtained by projecting each of the 3D CT data in the geometry of the on-board imager of TrueBeam™ system (Varian Medical System, Palo Alto, CA). In the second experiment, a lung cancer patient is chosen with two independent treatment planning 4D CT scans acquired at two different times with the same imaging parameter settings as above. Using the data-augmentation strategy described above, the first 4D-CT is used to generate training (2,400 samples) and validation (600 samples) datasets, whereas the second 4D CT was used to generate a testing dataset (200 samples). For each of the images in the training and testing datasets, the corresponding 2D projections are produced by projecting the 3D-CT volume in the geometry of the on-board imager of the TrueBeam™ system. To build a reliable model, the training and testing datasets might come from the same data distribution, but the datasets are independently sampled. The data acquisition and processing for the head-and-neck case are described in Supplementary Information.
Image preprocessing.
Data are preprocessed before feeding them into the network. First, we resize all data samples to the same size. For example, all the 2D projection images are reshaped to . The volumetric images of the abdominal-CT and the lung-CT are resized to and respectively, due to their different depths in the z-axis. Each data sample is a pair of 2D projected view(s) and the corresponding 3D-CT. Similar to other deep-learning-based imaging studies15, down-sampling is introduced purely because of the memory limitation and for the purpose of computational efficiency. The formulation and algorithm are scalable to full-size images (512×512), because the component layers used in our model are also scalable to images of different sizes. At the current resolution of 128×128 (which is the same as that used in the deep-learning-based MRI reconstruction15), small motions of less than 3 mm may not be described accurately. However, we should emphasize that this resolution does not represent a fundamental limit of the deep-learning-based approach and can be improved as computational technology advances. In practice, methods such as deep-learning-based super-resolution are being actively pursued, which may be employed to improve the spatial resolution of the approach. Additionally, following the standard protocol of data pre-processing, we conduct scaling normalization for both the 2D projections and the 3D volumetric images, where pixel-wise or voxel-wise intensities are normalized to the interval . Moreover, we normalize the statistical distribution of the pixel-wise intensity values in the input 2D projections to be closer to a standard Gaussian distribution . Specifically, we calculate the statistical mean and standard derivation among all the training data. When a new sample was inputted, we subtract the mean value from the input image(s) and divide the image(s) by the standard derivation to get the input 2D image(s).
Training details.
With input images containing a stacked sequence of 2D projections, we train the deep network to predict the volumetric images , which is expected to be as close as possible to the ground-truth images . We define the cost function as the mean squared error (MSE) between the prediction and the ground truth , and the model was optimized by stochastic gradient descent iteratively. For comparison, we used the same training strategy and hyper-parameters for all experiments. We implemented the network by using the PyTorch52 library, and used the Adam optimizer53 to minimize the loss function and to update the network parameters iteratively through back-propagation. A learning rate of 0.00002 and a mini-batch size of 1 are used because of memory limitations. At the end of each training epoch, the model is evaluated on the validation set. This strategy is commonly used to monitor the model performance and avoid overfitting the training data. In addition, the learning rate is scheduled to decay according to the validation loss. Specifically, if the validation loss remains unchanged for 10 epochs, the learning rate is reduced by a factor 2. Finally, the best checkpoint model with the smallest validation loss is saved as the final model in the experiments. We trained the network using one Nvidia Tesla V100 graphics processing unit (GPU) for 100 epochs (duration typically around 20 hours for the abdominal-CT case). During testing, the typical inference time for 3D reconstruction of one testing sample is around 0.5 seconds.
Evaluation.
To evaluate the performance of the approach, we deploy the trained model on a testing dataset, and analyze the reconstruction results using both qualitative and quantitative evaluation metrics. We use four different metrics to measure the quality of predicted 3D images: mean absolute error (MAE), root mean squared error (RMSE), structural similarity (SSIM)54, and peak signal-to-noise-ratio (PSNR). We compute the average values across all testing samples, and they are shown in Table 1. MAE / MSE is the L1-norm / L2-norm error between and . As usual, we take the square root of MSE to get RMSE. In practice, MAE and RMSE are commonly used to estimate the difference between the prediction and ground-truth images. SSIM score is calculated with a windowing approach in an image, and is used for measuring the overall similarity between two images. In general, a lower value of MAE and RMSE or a higher SSIM score indicates a better prediction closer to the ground-truth images. PSNR is defined as the ratio between the maximum signal power and the noise power that affects the image quality. PSNR is widely used to measure the quality of image reconstruction.
Comparison study.
To better benchmark the proposed method against the existing techniques, we conduct a comparative study with the published principal component analysis (PCA)-based method55–57 and elaborate the difference and advantages of our proposed approach. The comparison is done for a special situation of 4D-CT reconstruction (abdominal CT) where the anatomical motion may be characterized by principal components. We find that the PCA and deep learning-based methods produce similar results in an ideal case when there is no inter-scan variation in patient positioning (since the results are very similar, the resultant images are not shown). However, the deep learning model outperforms the PCA method in more realistic scenarios when the patient position deviates slightly from that of the reference scan (see Supplementary Information for details).
Reporting summary.
Further information on research design is available in the Nature Research Reporting Summary linked to this article.
Supplementary Material
Acknowledgements
This research is partially supported by NIH (R01CA176553 and R01EB016777). The contents of this article are solely the responsibility of the authors and do not necessarily represent the official NIH views.
Footnotes
Data availability
The authors declare that the main data supporting the results in this study are available within the paper and its Supplementary Information. The raw datasets from Stanford Hospital are protected because of patient privacy yet can be made available upon request provided that approval is obtained after an Institutional Review Board procedure at Stanford.
Code availability
The source code of the deep-learning algorithm is available for research uses at https://github.com/liyues/PatRecon.
Competing interests
The authors declare no competing interests.
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Candes EJ, Romberg JK & Tao T Stable signal recovery from incomplete and inaccurate measurements. Commun. Pure Appl. Math 59, 1207–1223 (2006). [Google Scholar]
- 2.Lustig M, Donoho D & Pauly JM Sparse MRI: The application of compressed sensing for rapid MR imaging. Magn. Reson. Med 58, 1182–1195 (2007). [DOI] [PubMed] [Google Scholar]
- 3.Sidky EY & Pan X Image reconstruction in circular cone-beam computed tomography by constrained, total-variation minimization. Phys. Med. Biol 53, 4777–4807 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Chen GH, Tang J & Leng S Prior image constrained compressed sensing (PICCS): a method to accurately reconstruct dynamic CT images from highly undersampled projection data sets. Med. Phys 35, 660–663 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Yu H & Wang G Compressed sensing based interior tomography. Phys. Med. Biol 54, 2791–2805 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Choi K et al. Compressed sensing based cone-beam computed tomography reconstruction with a first-order method. Med. Phys 37, 5113–5125 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Fessler JA & Rogers WL Spatial resolution properties of penalized-likelihood image reconstruction: space-invariant tomographs. IEEE Trans. Image Process 5, 1346–1358 (1996). [DOI] [PubMed] [Google Scholar]
- 8.Ji S, Xue Y & Carin L Bayesian compressive sensing. IEEE Trans. Signal Process 56, 2346–2356 (2008). [Google Scholar]
- 9.Engl HW, Hanke M & Neubauer A Regularization of inverse problems Vol. 375 (Springer Science & Business Media, 1996). [Google Scholar]
- 10.Stayman JW & Fessler JA Regularization for uniform spatial resolution properties in penalized-likelihood image reconstruction. IEEE Trans. Med. Imaging 19, 601–615 (2000). [DOI] [PubMed] [Google Scholar]
- 11.Jiang M & Wang G Convergence studies on iterative algorithms for image reconstruction. IEEE Trans. Med. Imaging 22, 569–579 (2003). [DOI] [PubMed] [Google Scholar]
- 12.Wang J, Li T, Lu H & Liang Z Penalized weighted least-squares approach to sinogram noise reduction and image reconstruction for low-dose X-ray computed tomography. IEEE Trans. Med. Imaging 25, 1272–1283 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Xu Q et al. Low-dose X-ray CT reconstruction via dictionary learning. IEEE Trans. Med. Imaging 31, 1682–1697 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Preiswerk F et al. Hybrid MRI-Ultrasound acquisitions, and scannerless real-time imaging. Magn. Reson. Med 78, 897–908 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Zhu B, Liu JZ, Cauley SF, Rosen BR & Rosen MS Image reconstruction by domain-transform manifold learning. Nature 555, 487–492 (2018). [DOI] [PubMed] [Google Scholar]
- 16.Henzler P, Rasche V, Ropinski T & Ritschel T Single-image Tomography: 3D Volumes from 2D Cranial X-Rays. Computer Graphics Forum 37, 377–388 (2018). [Google Scholar]
- 17.Montoya JC, Zhang C, Li K & Chen G In Proc. SPIE 10948, Medical Imaging 2019: Physics of Medical Imaging, 1094826 (2019). [Google Scholar]
- 18.Nomura Y, Xu Q, Shirato H, Shimizu S & Xing L Projection-domain scatter correction for cone beam computed tomography using a residual convolutional neural network. Med. Phys 46, 3142–3155 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Wu Y et al. Incorporating prior knowledge via volumetric deep residual network to optimize the reconstruction of sparsely sampled MRI. Magn. Reson. Imaging In Press (2019). [DOI] [PMC free article] [PubMed]
- 20.Eslami SA et al. Neural scene representation and rendering. Science 360, 1204–1210 (2018). [DOI] [PubMed] [Google Scholar]
- 21.LeCun Y, Bengio Y & Hinton G Deep learning. Nature 521, 436–444 (2015). [DOI] [PubMed] [Google Scholar]
- 22.Schmidhuber J Deep learning in neural networks: An overview. Neural Netw 61, 85–117 (2015). [DOI] [PubMed] [Google Scholar]
- 23.Krizhevsky A, Sutskever I & Hinton GE Imagenet classification with deep convolutional neural networks. Advances in neural information processing systems, 1097–1105 (2012).
- 24.Simonyan K & Zisserman A Very deep convolutional networks for large-scale image recognition. arXiv preprint arXiv:1409.1556 (2014).
- 25.Shen L, Yeung S, Hoffman J, Mori G & Fei-Fei L Scaling Human-Object Interaction Recognition through Zero-Shot Learning. 2018 IEEE Winter Conference on Applications of Computer Vision (WACV), 1568–1576 (2018). [Google Scholar]
- 26.Chen C, Seff A, Kornhauser A & Xiao J Deepdriving: Learning affordance for direct perception in autonomous driving. Proceedings of the IEEE International Conference on Computer Vision, 2722–2730 (2015). [Google Scholar]
- 27.Collobert R & Weston J A unified architecture for natural language processing: Deep neural networks with multitask learning. Proceedings of the 25th international conference on Machine learning, 160–167 (2008). [Google Scholar]
- 28.Ibragimov B, Toesca D, Chang D, Koong A & Xing L Development of deep neural network for individualized hepatobiliary toxicity prediction after liver SBRT. Med. Phys, 4763–4774 (2018). [DOI] [PMC free article] [PubMed]
- 29.Poplin R et al. Prediction of cardiovascular risk factors from retinal fundus photographs via deep learning. Nat. Biomed. Eng 2, 158–164 (2018). [DOI] [PubMed] [Google Scholar]
- 30.Esteva A et al. Dermatologist-level classification of skin cancer with deep neural networks. Nature 542, 115–118 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Gulshan V et al. Development and validation of a deep learning algorithm for detection of diabetic retinopathy in retinal fundus photographs. JAMA 316, 2402–2410 (2016). [DOI] [PubMed] [Google Scholar]
- 32.Ting DSW et al. Development and validation of a deep learning system for diabetic retinopathy and related eye diseases using retinal images from multiethnic populations with diabetes. JAMA 318, 2211–2223 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Liu F et al. Deep convolutional neural network and 3D deformable approach for tissue segmentation in musculoskeletal magnetic resonance imaging. Magn. Reson. Med 79, 2379–2391 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Zhao W et al. Incorporating imaging information from deep neural network layers into image guided radiation therapy (IGRT). Radiother. Oncol 140, 167–174 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Liu F, Feng L & Kijowski R MANTIS: Model-Augmented Neural neTwork with Incoherent k-space Sampling for efficient MR parameter mapping. Magn. Reson. Med 82, 174–188 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Zhao W et al. Markerless pancreatic tumor target localization enabled by deep learning. Int. J. Radiat. Oncol. Biol. Phys In Press (2019). [DOI] [PMC free article] [PubMed]
- 37.Hoo-Chang S et al. Deep convolutional neural networks for computer-aided detection: CNN architectures, dataset characteristics and transfer learning. IEEE Trans. Med. Imaging 35, 1285–1298 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.van der Maaten L & Hinton G Visualizing data using t-SNE. J. Mach. Learn. Res 9, 2579–2605 (2008). [Google Scholar]
- 39.Papernot N, McDaniel P & Goodfellow I Transferability in machine learning: from phenomena to black-box attacks using adversarial samples. Preprint at arXiv:1605.07277 (2016).
- 40.Eykholt K et al. Robust physical-world attacks on deep learning models. Preprint at arXiv:1707.08945 (2017).
- 41.Metzen JH, Genewein T, Fischer V & Bischoff B On detecting adversarial perturbations. Preprint at arXiv:1702.04267 (2017).
- 42.Lee K, Lee H, Lee K & Shin J Training confidence-calibrated classifiers for detecting out-of-distribution samples. Preprint at arXiv:1711.09325 (2017).
- 43.Akhtar N & Mian A Threat of adversarial attacks on deep learning in computer vision: A survey. IEEE Access 6, 14410–14430 (2018). [Google Scholar]
- 44.Lee K, Lee K, Lee H & Shin J A simple unified framework for detecting out-of-distribution samples and adversarial attacks. In Proc. 31st Conference on Advances in Neural Information Processing Systems 7167–7177 (2018). [Google Scholar]
- 45.Su J, Vargas DV & Sakurai K One pixel attack for fooling deep neural networks. IEEE Trans. Evol. Comput. In Press (2019). [Google Scholar]
- 46.Yuan X, He P, Zhu Q & Li X Adversarial examples: Attacks and defenses for deep learning. IEEE Trans. Neural Netw. Learn. Syst. In Press (2019). [DOI] [PubMed] [Google Scholar]
- 47.Hinton GE & Salakhutdinov RR Reducing the dimensionality of data with neural networks. Science 313, 504–507 (2006). [DOI] [PubMed] [Google Scholar]
- 48.He K, Zhang X, Ren S & Sun J Deep Residual Learning for Image Recognition. In Proceedings of the IEEE conference on computer vision and pattern recognition 770–778 (2016). [Google Scholar]
- 49.Ioffe S & Szegedy C Batch normalization: Accelerating deep network training by reducing internal covariate shift. Preprint at arXiv:1502.03167 (2015).
- 50.Nair V & Hinton GE Rectified Linear Units Improve Restricted Boltzmann Machines. In Proceedings of the 27th international conference on machine learning (ICML-10) 807–814 (2010). [Google Scholar]
- 51.Isola P, Zhu J-Y, Zhou T & Efros A Image-to-image translation with conditional adversarial networks. In Proceedings of the IEEE conference on computer vision and pattern recognition 1125–1134 (2017). [Google Scholar]
- 52.Paszke A et al. Automatic differentiation in pytorch. In Proc. 30th Conference on Advances in Neural Information Processing Systems Autodiff Workshop (2017). [Google Scholar]
- 53.Kingma DP & Ba J Adam: A method for stochastic optimization. Preprint at arXiv:1412.6980 (2014).
- 54.Wang Z, Bovik AC, Sheikh HR & Simoncelli EP Image quality assessment: from error visibility to structural similarity. IEEE Trans. Image Process 13, 600–612 (2004). [DOI] [PubMed] [Google Scholar]
- 55.Li R et al. Real-time volumetric image reconstruction and 3D tumor localization based on a single x-ray projection image for lung cancer radiotherapy. Med. Phys 37, 2822–2826 (2010). [DOI] [PubMed] [Google Scholar]
- 56.Li R et al. 3D tumor localization through real-time volumetric x-ray imaging for lung cancer radiotherapy. Med. Phys 38, 2783–2794 (2011). [DOI] [PubMed] [Google Scholar]
- 57.Xu Y et al. A method for volumetric imaging in radiotherapy using single x-ray projection. Med. Phys 42, 2498–2509 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.