Abstract
To determine why elements of central pattern generators phase lock in a particular pattern under some conditions but not others, we tested a theoretical pattern prediction method. The method is based on the tabulated open loop pulsatile interactions of bursting neurons on a cycle-by-cycle basis and was tested in closed loop hybrid circuits composed of one bursting biological neuron and one bursting model neuron coupled using the dynamic clamp. A total of 164 hybrid networks were formed by varying the synaptic conductances. The prediction of 1:1 phase locking agreed qualitatively with the experimental observations, except in three hybrid circuits in which 1:1 locking was predicted but not observed. Correct predictions sometimes required consideration of the second order phase resetting, which measures the change in the timing of the second burst after the perturbation. The method was robust to offsets between the initiation of bursting in the presynaptic neuron and the activation of the synaptic coupling with the postsynaptic neuron. The quantitative accuracy of the predictions fell within the variability (10%) in the experimentally observed intrinsic period and phase resetting curve (PRC), despite changes in the burst duration of the neurons between open and closed loop conditions.
INTRODUCTION
Central pattern generators (CPGs) are neural circuits able to maintain a functionally relevant rhythmic output without requiring input from external sources. To uncover the fundamental principles of operation that allow a CPG to maintain a particular pattern despite a wide variation in the parameters relevant to the oscillation, such as frequency as well as specific neuronal and synaptic parameters, we have previously developed methods to predict the patterns exhibited in the closed loop circuit from the phase resetting curves (PRCs) measured for each component in the open loop configuration. In the open loop configuration the synaptic coupling is unidirectional (Fig. 1, C and D, insets), whereas in the closed loop configuration the two neurons are reciprocally coupled (Fig. 2, insets). These methods have been successfully applied in the noise-free environment of purely model circuits (Canavier et al., 1997, 1999; Luo et al., 2004). To determine whether similar methods can be successfully applied in the presence of the inevitable variability in biological systems, we applied the methods to hybrid circuits constructed with one biological and one model neuron each. Since our phase resetting methods apply only to endogenous bursters, we constructed the simplest possible pattern generating circuit that is composed only of endogenous bursters and contains a biological neuron (Fig. 1 B). The biological neuron selected was a pharmacologically isolated pyloric dilator (PD) neuron in the Homarus americanus stomatogastric ganglion (STG), reciprocally coupled to a model neuron using the dynamic clamp (Sharp et al., 1993a,b).
FIGURE 1.
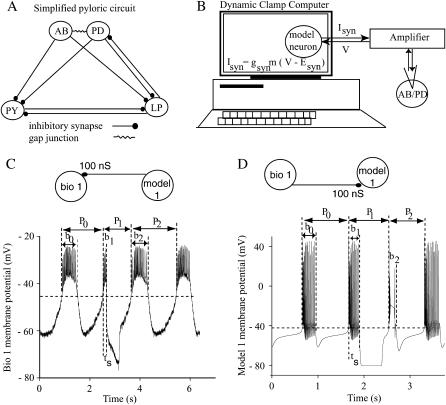
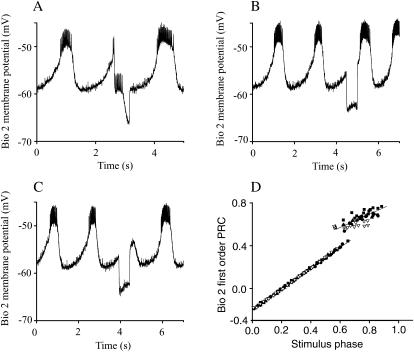
Experimental setup. (A) Simplified pyloric circuit. The pyloric network consists of 14 neurons, which can be grouped as follows: the anterior burster neuron (AB), two pyloric dilator neurons (PD), eight pyloric neurons (PY), and one lateral pyloric neuron (LP). (B) A schematic representation of the dynamic clamp experiment. A pharmacologically isolated AB/PD complex was impaled with conventional sharp microelectrodes via a single PD neuron, and the membrane potential (V) recorded from the PD neuron is used to determine how much synaptic current (Isyn) this neuron receives through the artificial synapse. (C) Phase resetting in a biological neuron. The membrane potential record from a free running AB/PD complex, with an intrinsic period P0, is perturbed at the stimulus interval ts by an inhibitory synaptic input with gmodel1>bio1 = 100 nS and a duration of 500 ms. An upward crossing of the voltage threshold (horizontal dashed line at −45 mV) is defined as the beginning of the burst and assigned a phase of zero. As a result of this particular perturbation, the first burst after the perturbation is advanced such that P1 < P0. The length of the second cycle is P2 ≅ P0, which implies that the second order resetting in this case is negligible. (D) Phase resetting in a model neuron. In this example, a strong inhibitory perturbation with gbio1>model1 = 100 nS and a burst duration of 500 mS, applied during the burst of model neuron 1, terminates the ongoing burst. The length of the perturbed cycle P1 is not significantly altered, but the burst length (b1) in the cycle that contains the perturbation is shortened, as is the length of the cycle after the perturbation and the burst (b2) in that cycle. The burst threshold for this model neuron was −42 mV (horizontal dashed line).
FIGURE 2.
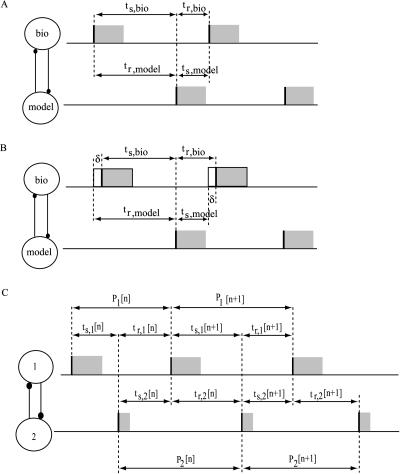
Schematic representation of an alternating 1:1 firing mode in a two-neuron network. The stimulus interval of the neuron j is ts,j, and its recovery interval is tr,j. (A) Steady firing in a two-neuron network with no delays. The stimulus interval of one neuron equals the recovery interval of the other. The burst onset is marked with a vertical thick solid line. Although this analysis treats the coupling as pulsatile and ignores burst duration, the burst durations are indicated by solid rectangles to emphasize that this analysis applies to bursting neurons as long as the assumptions are not violated. (B) Steady firing in a two-neuron network with delay. A delay δ between the activation of the synaptic coupling from the biological neuron to the model neuron and the initiation of a burst in the model neuron requires a restatement of the periodicity criteria: tr,model = ts,bio + δ, and ts,model = tr,bio − δ. (C) Convergence to a steady alternating 1:1 phase-locked mode. The equivalence of certain intervals as shown here results in the periodicity constraints that must be satisfied in successive cycles during convergence to (or divergence from) an assumed steady alternating phase-locked mode. These constraints can be used to derive a system of coupled difference equations, or maps, for the time evolution of the system on a cycle-to-cycle basis.
The PD neuron is a component of the pyloric circuit of the crustacean STG in H. americanus, which controls the movements of the pylorus (Bal et al., 1988; Bartos and Nusbaum, 1997; Harris-Warrick et al., 1992; Marder and Calabrese, 1996; Marder, 1998; Mulloney, 1977; Weaver and Hooper, 2003). The complete pyloric circuit consists of 14 neurons, but often a functional grouping of the neurons (Hartline and Gassie, 1979; Hartline, 1979) allows a reduction to three essential nodes (Fig. 1 A) that generate the triphasic firing pattern of the pyloric cycle. Because of the electrical coupling between the anterior burster (AB) pacemaker neuron and the two PD neurons, we will consider them as a single functional unit called the AB/PD complex (Fig. 1 A). The AB/PD complex strongly inhibits the other cells in the circuit, acting as the overall frequency controller for the network (Mulloney, 1977; Miller and Selverston, 1982).
We have focused on endogenous bursters because they play a central role in numerous CPGs including the pyloric circuit (Hartline and Gassie, 1979; Hartline, 1979; Miller and Selverston, 1982), the heartbeat of crustaceans (Tasaki and Cooke, 1990), the gastric CPGs of the crustacean stomatogastric system (Harris-Warrick et al., 1992; Panchin et al., 1993; Selverston and Moulins, 1987), and the feeding CPG in mollusks (Arshavsky et al., 1989, 1991). An endogenous burster oscillates autonomously with a cycle length equal to its intrinsic period and responds to external inputs by prolonging or shortening the cycle length (Glass and Mackey, 1988; Perkel et al., 1964; Winfree, 1987) as in Fig. 1, C and D. The response of a limit cycle oscillator to a single input event depends on the timing (phase), amplitude, and duration of the perturbation. The unperturbed period is indicated by P0 and the intrinsic burst duration by b0 (Fig. 1, C and D). A hyperpolarizing perturbation of a significant duration was applied during the cycle labeled P1. The stimulus interval (ts) is defined as the time elapsed between the start of the burst and the beginning of the input stimulus. In the open loop configuration, the stimulus phase (ϕ) is equal to the stimulus interval normalized by the intrinsic period (ts/P0). A phase of zero is assigned to the beginning of the burst. The PRC measures the change in the length of the cycle recorded as a function of the phase at which the perturbation is received. We define the first order phase resetting F1(ϕ) as P1/P0 − 1 and the second order phase resetting F2(ϕ) as P2/P0 − 1 (Fig. 1, C and D).
It is important to recognize the distinction between the PRC here and the infinitesimal PRC that, in theory (Ermentrout, 1996; Hoppensteadt and Izhikevich, 1997; Kopell and Ermentrout, 1988; Mirollo and Strogatz, 1990), could be convolved with the waveform of the perturbation to obtain the total resetting. In the circuits we study, a burst in the presynaptic neuron causes phase space excursions in the postsynaptic neuron far from the limit cycle; therefore it is not valid to sum over a set of infinitesimal perturbations. Instead, we treat the entire perturbation as a whole, which converts our analysis to a mapping on a cycle-by-cycle basis. Therefore, in an analogy with spike time response (STR) methods (Acker et al., 2003), the PRCs in this study can be referred to as burst PRCs, to distinguish them from the infinitesimal PRC used by others.
We have successfully analyzed model circuits (Canavier et al., 1997, 1999) under the following assumptions: 1), all component neurons in the circuit are endogenous bursters, 2), there are no synaptic delays, 3), each neuron receives one perturbation (synaptic input) per cycle, 4), this perturbation takes the same form in the closed loop circuit as in an open loop circuit composed only of a presynaptic neuron driving a postsynaptic one, and 5), each neuron returns close to its unperturbed limit cycle before the next input is received. The last condition is required for the phase to be well defined.
Here we test the effectiveness of the burst PRC in predicting 1:1 phase-locked modes in two-neuron hybrid networks over a wide range of synaptic couplings from weak (1 nS) to strong (1000 nS), and stimulus durations ranging from 0.28 s to 1.06 s, which represents a range of 20–80% of the intrinsic period of the relevant postsynaptic neuron. The quantitative accuracy of the predictions fell within the variability (10%) in the experimentally observed intrinsic period and PRC, despite changes in the burst duration of the neurons between open and closed loop conditions. Consideration of not only the first but also the second order phase resetting improved the quantitative accuracy, and in some cases was required for qualitative accuracy of the predictions.
MATERIALS AND METHODS
Electrophysiology
H. americanus were purchased from Yankee Lobster (Boston, MA) and maintained in artificial seawater at 10–12°C until used. The stomatogastric nervous system (STNS) was dissected out and pinned out in a dish coated with Sylgard (Dow Corning, Midland, MI), and the STG was desheathed with fine forceps. Throughout the experiments, the stomatogastric nervous system was superfused with chilled (9–14°C) saline containing (in mM) NaCl, 479.12; KCl, 12.74; CaCl2, 13.67; MgSO4, 20; Na2SO4, 3.91; HEPES, 5; pH 7.45. Extracellular recordings were made with stainless steel pin electrodes in Vaseline wells on the motor nerves and amplified with a differential AC amplifier (Model 1700, A-M Systems, Carlsborg, WA). Intracellular recordings from cells in the STG were obtained with an Axoclamp 2B amplifier (Axon Instruments, Foster City, CA) in discontinuous current clamp mode using microelectrodes filled with 0.6 M K2SO4 and 20 mM KCl; electrode resistances were in the range of 20–40 MΩ. Extracellular and intracellular potential traces were digitized with a Digidata 1200A board (Axon Instruments), recorded using Clampex 8.0 software (Axon Instruments), and analyzed with in-house software. The PD and lateral pyloric (LP) motor neurons were identified based on their membrane potential waveforms, the timing of their activity in the pyloric rhythm, and their axonal projections to the appropriate motor nerves. The only synaptic feedback to the pyloric pacemaker group through the LP to PD inhibitory synapse was removed by applying 10−5 M picrotoxin in the bath. The pharmacologically isolated pyloric pacemaker was monitored by impaling one of the PD neurons; it served as the biological oscillator in the experiments reported here.
Dynamic clamp
We recorded the membrane potential of the AB/PD complex and used the dynamic clamp (Sharp et al., 1993a,b) to replace the synaptic input from LP onto PD with artificial synaptic inputs: the membrane potential V at the PD cell body was amplified, fed into a Digidata 1200A board (Axon Instruments), and digitized at a rate of 1.7 kHz with in-house software modified from a C++ program kindly provided by R. Pinto (Pinto et al., 2001). The dynamic clamp program detected bursts in the ongoing PD rhythm and monitored the instantaneous period. Artificial dynamic clamp synaptic inputs were generated at different phases of the PD rhythm by setting the synaptic activation to the desired value for the desired duration. During the synaptic input, the program computed the momentary synaptic current as described below. To inject this synaptic current into the PD neuron, the program computed the corresponding command voltage, which was turned into an analog voltage by the Digidata board and sent to the electrode amplifier.
Model neurons
The model neurons had a single compartment with eight Hodgkin-Huxley type membrane currents and an intracellular calcium buffer. The membrane currents were based on voltage-clamp experiments on lobster stomatogastric neurons (Turrigiano et al., 1995) and included a fast sodium current (INa), a fast and a slow transient calcium current (ICaT and ICaS), a fast transient potassium current (IA), a calcium-dependent potassium current (IKCa), a delayed rectifier potassium current (IKd), and a leak current (Ileak). The model neurons used here had identical current dynamics and differed only in the maximal conductances of their eight membrane currents; these conductances were chosen to produce different burst periods, durations, and duty cycles in the different model neurons. The maximal conductances of the eight currents and the corresponding intrinsic periods and burst durations for all seven model neurons considered in this study are listed in Table 1 in the Supplementary Material. The model was described in detail in Prinz et al. (2003), and similar models have been used before (Goldman et al., 2001; Liu et al., 1998). The model was implemented in a C++ program, and all differential equations were integrated with an exponential Euler method at a time resolution of ∼50 μs, corresponding to 10 updates of the model neuron for every voltage value read and current command written by the dynamic clamp.
TABLE 1.
Experimentally observed and predicted phase-locked modes in four experiments using both the first and second order PRCs
|
gbio>model
|
|||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Model neuron | Bio | gmodel>bio | 1 | 2 | 3 | 5 | 10 | 20 | 30 | 50 | 100 | 200 | 300 | 500 | 1000 |
| 1 | 1 | 100 | c/– | c/a | a/a | a/a | a/a | a/a | a/a | a/a | a/a | a/a | a/a | a/a | a/a |
| 2 | 300 | a/a | a/a | a/a | a/a | a/a | a/a | a/a | a/a | a/a | a/a | a/a | a/a | a/a | |
| 4 | 500 | a/a | a/a | a/a | a/a | a/a | a/a | a/a | |||||||
| 2 | a/a | a/a | a/a | a/a | |||||||||||
| 1 | a/a | a/a | a/a | a/a | |||||||||||
| 2 | 3 | 30 | a/a | a/a | a/a | a/a | a/a | a/a | a/a | a/a | a/a | a/a | a/a | a/a | a/a |
| 1 | 100 | a/a | a/a | a/a | a/a | a/a | a/a | a/a | |||||||
| 3 | a/a | a/a | a/a | a/a | a/a | a/a | a/a | ||||||||
| 4 | a/a | a/a | a/a | a/a | |||||||||||
| 3 | 1 | 100 | a/a | a/a | a/a | a/a | a/a | a/a | a/a | a/a | a/a | a/a | a/a | a/a | a/a |
| 2 | 500 | a/a | a/a | a/a | a/a | a/a | a/a | a/a | a/a | a/a | a/a | ||||
| 1 | a/a | a/a | a/a | a/a | |||||||||||
| 4 | 1 | 50 | c/– | c/– | a/a | c/– | c/– | c/– | a/a | c/– | c/– | c/– | a/a | c/– | c/– |
| 1 | 100 | c/– | c/– | a/a | c/– | c/– | c/– | a/a | c/– | c/– | c/– | a/a | c/– | c/– | |
| 2 | a/a | a/a | a/a | a/a | |||||||||||
| 4 | a/a | a/a | a/a | a/a | |||||||||||
| 5 | 1 | 100 | c/a | c/a | a/a | a/a | a/a | a/a | a/a | a/a | a/a | a/a | |||
| 6 | 3 | 30 | a/a | a/a | a/a | a/a | a/a | a/a | a/a | ||||||
| 7 | 2 | 30 | a/a | a/a | a/a | a/a | a/a | a/a | a/a | ||||||
| 4 | 100 | a/a | a/a | a/a | a/a | a/a | a/a | a/a | |||||||
For each gmodel>bio (third column), 10 hybrid networks were formed with the first biological neuron, and seven with the other three biological neurons. For each hybrid circuit characterized by a pair (gmodel>bio, gbio>model), the experimental versus predicted results are separated by a slash: the numerator is the experimentally observed phase-locked mode, and the denominator is the predicted pattern. All conductances are in nanoSiemens. The phase-locked modes are marked by “a” for 1:1, “c” for a complex 2:1/1:1 mode, and “–” for no mode. Mismatches between experiment and prediction are marked in bold.
Artificial synapses
For all synapses simulated here, the synaptic current was Isyn = gsynm (Vpostsyn − Erev) where gsyn is the conductance of the synapse, m is the synaptic activation, Vpostsyn is the membrane potential of the postsynaptic neuron, and Erev is the synaptic reversal potential, which was set to −90 mV for all synapses based on voltage clamp experiments on the LP to PD synapse (Thirumalai, 2002). All synapses were instantaneously activating and deactivating. The synaptic activation function, 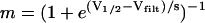 , was chosen such that the synapse is fully activated during the burst and deactivated between bursts.
, was chosen such that the synapse is fully activated during the burst and deactivated between bursts.
Because the potential between spikes reaches very hyperpolarized levels, and the activation of the synapses is instantaneous, we used a filtered version, Vfilt, of the presynaptic membrane potential to compute the synapse activation to smooth it. For every time step Δt, Vfilt was updated according to Vfilt(t + Δt) = Vfilt(t) + (Vfilt(t + Δt) − Vfilt(t))Δt/τfilt, where τfilt = 1 ms for the biological neuron. The value of V1/2 = −45 mV for synapses from the biological neurons was set below the minimal filtered voltage between spikes within a burst. We chose s = 0.1 mV for all synapses, which ensured rapid activation and deactivation of the synapse during the up- and downstrokes of each presynaptic burst. For synapses from model neurons, the values of V1/2, and the corresponding filtering constants, τfilt, were chosen such that the synapse remained fully activated throughout the burst, even during the hyperpolarized intervals between spikes. The chosen values ranged from −47 mV to −40 mV for V1/2 and from 10 mS to 30 ms for τfilt (Table 2 in the Supplementary Material).
TABLE 2.
Stability analysis
| gbio>model | ϕbio | ϕmodel | m1bio | m2bio | m1model | m2model | λ | λ1/λ2 | Max{|λ|} |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.42 | 0.698 | 0.474 | 0.005 | 0.999 | −0.032 | 0.000 | 0.032/−0.005 | 0.032 |
| 3 | 0.489 | 0.644 | 0.309 | −0.064 | 0.999 | −0.099 | 0.000 | 0.099/0.064 | 0.064 |
| 10 | 0.519 | 0.64 | 0.261 | −0.104 | 0.999 | −0.099 | 0.000 | 0.104/0.099 | 0.104 |
| 30 | 0.514 | 0.606 | 0.268 | −0.098 | 0.999 | −0.064 | 0.000 | 0.098/0.064 | 0.098 |
| 100 | 0.523 | 0.585 | 0.257 | −0.108 | 0.999 | −0.037 | 0.000 | 0.108/0.037 | 0.108 |
| 300 | 0.492 | 0.59 | 0.302 | −0.069 | 0.999 | −0.048 | 0.000 | 0.069/0.048 | 0.069 |
| 1000 | 0.504 | 0.592 | 0.282 | −0.084 | 0.999 | −0.05 | 0.000 | 0.084/0.05 | 0.084 |
The values of the predicted phase of the biological neuron 4 (ϕbio) and the model neuron 1 (ϕmodel) and the slopes of the first (m1) and second (m2) order PRCs for the hybrid network with gmodel1>bio4 = 100 nS. All conductances gbio4>model1 are in nanoSiemens. The root of the characteristic equation based on the first order PRC slope is λ = (1 − m1,bio)(1 − m1,model), and the values obtained using the second order PRC contribution are λ1/λ2 with the maximal absolute value Max{|λ|} (see Eq. 4).
PRCs for biological and model neurons
To generate the PRC of a biological neuron in response to synaptic input from a given model neuron and for a given synapse strength gmodel>bio, we first determined the intrinsic period P0 and burst duration b0 of the biological neuron from the filtered membrane potential recording of the unperturbed neuron of at least 20 s. We define the intrinsic period P0 of the biological neuron as the time between two successive crossings of the −45 mV voltage threshold with positive slope and the intrinsic burst duration b0 as the time between the voltage threshold crossing with positive slope and the following crossing with negative slope (Fig. 1 C). The intrinsic periods of the four biological neurons immediately before different couplings to model neurons ranged from 1.12 s to 2.5 s and their burst durations were between 0.44 s and 0.88 s (Table 3 in the Supplementary Material). Once the intrinsic period was determined, the membrane potential of the biological neuron in response to conductance pulses of amplitude gmodel>bio was recorded, using a stored activation profile of the artificial synapse, which corresponds to the activation produced by a single presynaptic burst in a model neuron in the open loop condition (no feedback). Individual stimuli were delivered ∼10 s apart to ensure that the biological neuron returned to its unperturbed activity between stimuli. The stimulus interval was computed by multiplying the desired stimulus phase by the period of the preceding cycle. For a full PRC, we delivered stimuli at 20 (for biological neuron 1) or 40 (for the other biological neurons) equally spaced phases between 0 and 1. Each PRC was recorded a total of four times. The experimental protocol described above was repeated for the same model neuron for all synaptic conductances gmodel>bio listed in Table 1 (third column). Once all synaptic conductances gmodel>bio were completed, the next model neuron was selected.
TABLE 3.
Mean prediction error and the corresponding SE of the recovery intervals compared to the experimental values
| Model | Bio | gmodel>bio | δtrbio | δtrmodel | Model | Bio | gmodel>bio | δtrbio | δtrmodel |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 100 | NA | NA | 3 | 1 | 500 | −10.0 ± 6.7 | 8.0 ± 11.7 |
| −10.2 ± 3.1 | 8.0 ± 3.3 | −6.1 ± 4.2 | 3.5 ± 4.8 | ||||||
| 1 | 1 | 500 | NA | NA | 3 | 2 | 100 | −9.8 ± 8.9 | −1.1 ± 9.2 |
| −1.0 ± 6.1 | 5.0 ± 4.3 | 4.2 ± 8.3 | −0.6 ± 9.2 | ||||||
| 1 | 2 | 100 | 7.8 ± 1.7 | −4.9 ± 1.9 | 4 | 1 | 50 | NA | NA |
| 4.2 ± 2.3 | −4.6 ± 1.7 | NA | NA | ||||||
| 1 | 2 | 300 | 8.7 ± 2.1 | −9.2 ± 1.1 | 4 | 1 | 100 | NA | NA |
| 5.1 ± 5.6 | −10.6 ± 0.7 | NA | NA | ||||||
| 1 | 4 | 100 | −0.7 ± 1.3 | −2.2 ± 1.9 | 4 | 2 | 100 | −9.3 ± 3.9 | −11.8 ± 11.5 |
| 1.3 ± 0.8 | −0.3 ± 1.1 | −2.2 ± 3.8 | −10.1 ± 5.2 | ||||||
| 2 | 1 | 100 | 5.0 ± 9.4 | −3.1 ± 8.4 | 4 | 4 | 100 | −6.9 ± 2.9 | 5.9 ± 1.2 |
| 2.5 ± 4.7 | −3.1 ± 6.1 | −6.5 ± 2.4 | 2.9 ± 1.5 | ||||||
| 2 | 3 | 30 | 11.5 ± 8.5 | −3.1 ± 3.8 | 5 | 1 | 100 | NA | NA |
| 6.1 ± 8.1 | −0.2 ± 3.6 | 6.0 ± 4.8 | −8.1 ± 2.4 | ||||||
| 2 | 3 | 100 | −5.8 ± 3.1 | 12.1 ± 1.6 | 6 | 3 | 30 | −4.7 ± 1.6 | 15.4 ± 2.8 |
| −7.2 ± 3.5 | 0.4 ± 1.4 | 4.6 ± 1.5 | 0.0 ± 5.1 | ||||||
| 2 | 4 | 100 | −13.2 ± 2.9 | 17.8 ± 1.1 | 7 | 2 | 30 | 25.2 ± 15.1 | −7.2 ± 4.3 |
| −13.0 ± 3.1 | 15.0 ± 0.7 | −4.4 ± 2.6 | 5.1 ± 3.3 | ||||||
| 3 | 1 | 100 | −15.0 ± 9.5 | 7.4 ± 8.5 | 7 | 4 | 100 | −23.2 ± 3.4 | 1.1 ± 5.0 |
| −5.0 ± 6.3 | 2.0 ± 3.2 | −8.4 ± 2.6 | −0.5 ± 1.2 |
For each gmodel>bio (third and ninth columns), 10 hybrid networks were formed with the first biological neuron and seven with each of the other three biological neurons. For each hybrid circuit characterized by a pair (gmodel>bio, gbio>model), the first line is the mean percent error based only on F1, and the second line is the mean percent error based on both F1 and F2. The values in bold correspond to the data summarized in Figs. 6 and 8. If no number is given (NA for not applicable), no 1:1 mode was predicted. A negative (positive) sign of the mean error indicates a systematic underestimation (overestimation) of the predicted recovery interval compared to the experimental value.
A similar experimental protocol was used to extract the PRCs for the model neurons at 40 equally spaced phases between 0 and 1. To obtain the PRCs of the bursting model neurons, we applied a synaptic input with a stored activation profile of the artificial synapse, which in this case corresponds to the activation produced by a single presynaptic burst in the biological neuron in the open loop condition (no feedback), at different times during the ongoing simulated rhythm. We assigned phase zero to the burst onset, which was specified by a voltage threshold of −42 mV (Fig. 1 D). Each PRC was recorded only once.
Dynamic-clamp generated hybrid circuits
We used the dynamic clamp to generate 164 different mutually inhibitory hybrid circuits between one of four biological neurons and one of seven model neurons (Fig. 1 B). The range of synaptic conductances used in our experiments encompasses the estimated physiological range of synaptic conductances onto the AB/PD complex in the STG (between 10 nS and 60 nS according to Thirumalai, 2002) and extends beyond the 500-nS limit considered in the existing implementations of analog two-neuron hybrid networks (Pinto et al., 2000). For each circuit, we recorded the membrane potential of the biological and the model neuron for at least 20 s before and 40 s after the synapses were switched on. The recording in the closed loop configuration was used to extract the experimental values of the relative burst timing of the biological and the model neuron as well as the phase-locked period.
Theoretical method
The theoretical method for predicting phase-locked modes has two components, existence and stability. Only modes that satisfy the periodicity constraints can exist, hence the existence criterion, and only those that are stable can be observed in the presence of the small perturbations that result from the unavoidable presence of noise, hence the stability criterion. The periodicity constraints (Canavier et al., 1997, 1999; Luo et al., 2004) include the assumptions that the steady-state phase-locked period of each neuron is determined by the closed loop phase resetting produced by the input from its partner (right-hand side of Eq. 1) and that this resetting is equal to that observed in the open loop condition. In addition, there is the obvious requirement that in 1:1 phase locking the period of each neuron must be the same and equal to the sum of the stimulus interval (ts) and the recovery interval (tr) for each neuron. The equivalence of the sum of the stimulus and recovery intervals with the period in the closed circuit can be stated as
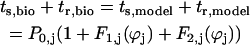 |
(1) |
,where the index j stands for bio or model neuron, and ϕbio and ϕmodel, represent the phase of each neuron, corresponding to the position on the appropriate unperturbed limit cycle at which an input is received. The stimulus interval (ts,j) is defined as the interval between the initiation of a burst in neuron j and the beginning of an input onto neuron j, and the recovery interval is defined as the interval between the beginning of an input onto neuron j and the initiation of the next burst in neuron j (Fig. 2 A). The first and second order PRCs can be used to predict the steady-state values of ts,j and tr,j as follows:
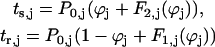 |
(2) |
.Since both of the above quantities depend solely upon the phase at which an input is received, one can plot the pair of points (tr,model, ts,model) for each value of ϕmodel as well the pair of points (ts,bio, tr,bio) for each value of ϕbio, discarding any resultant negative values for the intervals because they violate causality. Due to the choice of axes for these plots, the intersection(s) of these two curves at the periodicity criterion tr,bio = ts,model and ts,bio= tr,model will give the values of the stimulus and recovery times for which the periodicity constraints in Eq. 1 are satisfied for both values of j: model and bio. If there is a fixed time difference between the initiation of a presynaptic burst and the activation of the synaptic coupling to the postsynaptic neuron, then the receipt of the input by the postsynaptic neuron does not coincide with the initiation of the presynaptic burst. The stimulus and recovery intervals relative to burst onset are shown in Fig. 2 B for a particular case in which the coupling is activated before the first spike in the burst occurs, which could occur in the case of graded synaptic coupling. The periodicity criterion is now ts,model +δ = tr,bio and ts,bio +δ = tr,model, so one must plot the pairs (tr,model, ts,model + δ) and (ts,bio + δ, tr,bio) to obtain the intersection that satisfies this periodicity criterion.
The stability criteria were initially formulated by ignoring the contribution of second order resetting and using the first order PRC to define a mapping between the phases at which inputs are received in successive cycles in terms of the dependence of φj[n] on φj[n − 1] where n indicates the current cycle and n − 1 indicates the previous cycle. A mapping in terms of the stimulus and recovery intervals ts,j[n] and tr,j[n] is shown in Fig. 2 C, and due to the implicit dependence of these quantities on φj[n], the mapping can be written in terms of the φj[n]. If a steady state is assumed for both φmodel[∞] and φbio[∞], the mapping also gives the deviation of each phase, Δφj[n], from its steady-state value. This mapping can be linearized by assuming that the change in cycle period that occurs in cycle n due to a small perturbation in the previous cycle, Δφj[n − 1], can be given by m1,jΔφj[n − 1] where m1,j is the slope of the first order PRC F′1,j(φj[∞]) at the phase at which neuron j receives an input in the assumed steady 1:1 phase-locked mode. This leads immediately to the result of Dror et al. (1999) that Δφj[n] = (1 − m1,bio)(1 − m1,model)Δφj[n − 1]. The quantity (1 − m1,bio)(1 − m1,model) is a multiplier λ that determines whether a perturbation from the assumed steady 1:1 phase-locked mode will increase or decrease. If −1 < λ < 1, the perturbation will decrease to zero, guaranteeing the stability of the assumed 1:1 phase-locked mode. Thus the stability criterion if F2,j(φj) = 0 is −1 < (1 − m1,bio)(1 − m1,model) < 1. However, if F2,j(φj) ≠ 0, then two previous cycles (n − 1 and n − 2) must be taken into account. Using the same methodology, and defining m2,j as the slope of the second order PRC F′2,j(φj[∞]) at the phase that neuron j receives an input in the assumed steady 1:1 phase-locked mode, the future of a perturbation is given by a higher order discrete map because an additional cycle must be taken into account (Oprisan and Canavier, 2001):
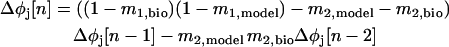 |
(3) |
.To guarantee stability, meaning that perturbations die out and go to zero, the solutions to the characteristic equation of Eq. 3, i.e.,
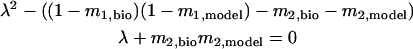 |
(4) |
,which are λ1 and λ2, both must be in the range from −1 to 1 for the presumed 1:1 phase-locked mode to be stable. Note that by neglecting the contribution of the second order PRC in Eq. 4, i.e., setting both m2,model and m2,bio equal to zero, we recover the result of Dror et al. (1999) that λ = (1 − m1,bio)(1 − m1,model).
RESULTS
Phase resetting curves
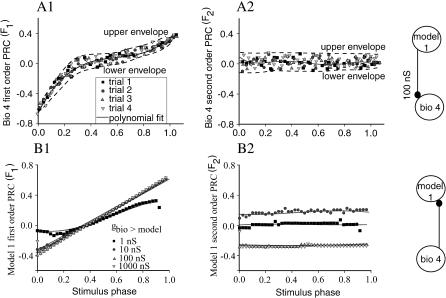
We extracted all PRCs from the membrane potential recordings offline, using a burst threshold of −45 mV for all biological neurons. For each synaptic coupling gmodel>bio, the average of the four PRCs was computed and approximated with a polynomial fit. The upper and lower envelopes reflect the trial-to-trial variability of biological neuron PRCs (dashed lines in Fig. 3, A1 and A2). The upper (lower) envelope is the polynomial fit through the maximal (minimal) values of the phase resetting measured in the four experiments versus the stimulus phase. Typical first order PRCs obtained for the biological neuron in the open loop setup are shown in Fig. 3 A1, and typical second order resetting curves are given in Fig. 3 A2. The results from the four different trials described in the Methods are indicated by different symbols, and the average resetting and both envelopes are shown. In general, the first order resetting consisted of advances early in the cycle associated with burst truncation followed by a shortened cycle, a flat region in the middle of the cycle, and delays near the end of the cycle as the subsequent burst was delayed by the prolonged inhibition. The observed first order resetting is consistent with previous work (Oprisan et al., 2003; Prinz et al., 2003), and because the applied perturbation is essentially a square pulse, the dependency of the PRC in the biological neuron on the particular model neuron used to drive it reduces to the different burst durations of the various models. Again consistent with previous work, the longer pulse durations reduce the extent of the nearly flat region in the middle in favor of a more uniformly linear PRC. The second order PRC for the biological neuron was in general essentially flat and equal to zero. Additional examples of PRCs for biological neurons are given in the Supplementary Material.
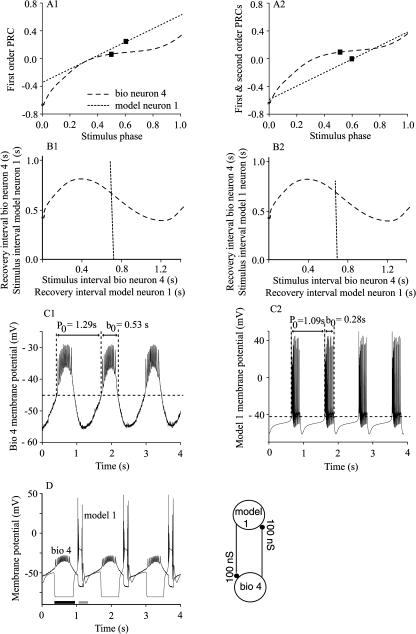
FIGURE 3.
Typical experimentally obtained phase resetting curves. (A) Biological neuron 4. (A1) The first order PRCs in response to a burst from model neuron 1. The synaptic strength was gmodel>bio = 100 nS, and the burst threshold was −45 mV. The experiments were repeated four times to reduce the trial-to-trial variability. (A2) The second order PRC shows no specific dependence on the stimulus phase. The best polynomial fits are shown as continuous lines. The minimal polynomial degree for the best fit of the first order PRCs was three (higher than 99% correlation with p < 0.05 confidence level) and nine for the second order PRCs. The upper and lower envelopes of the four trials are marked with dashed lines. (B) PRCs for model neuron 1 for four different values of gbio>model between 1 nS and 1000 nS. (B1) The first order PRCs for gbio>model > 20 nS are linear with a correlation coefficient higher than 99.9%, whereas PRCs for gbio>model ≤ 20 nS were best fitted by a third degree polynomial with a correlation coefficient higher than 99%. (B2) The second order PRCs show no specific dependence on the stimulus phase and a model-specific dependence on the synapse strength. The corresponding open loop circuits are schematically represented to the right of the PRC panels.
First order resetting curves are given for model neuron 1 in Fig. 3 B1 and second order in Fig. 3 B2. Here, only a single trial is shown, but trials at different values of the conductance gbio>model are indicated by different symbols. The first order resetting is typical of the model neuron PRCs in that at 1 nS for the gbio>model conductance the PRC has some curvature, but as the conductance is increased to 10 nS and above, the PRC saturates and becomes linear. This is likely due to the inhibition driving the model neuron to a fixed point (Demir et al., 1997) such that the burst follows the end of the perturbation by a fixed interval. As with the biological neuron, advances are observed early in the cycle and delays late in the cycle. The second order resetting in Fig. 3 B1 is typical of model neurons in that it is essentially flat and thus independent of phase with a slope near zero. It is also typical in that the value of the second order resetting is near zero at gbio>model = 1 nS, but at a higher value (10 nS), a delay is observed largely due to a lengthened burst in the second cycle. The second order resetting shown in Fig. 3 B2 is atypical in that the delay that constitutes the second order resetting usually saturates at higher conductances, but in the case of model 1 at large conductance values (above 100 nS) an advance is observed. This advance is largely due to burst shortening in the subsequent cycle, as observed for the same model neuron driven by a different biological neuron in Fig. 1 D. Additional examples of resetting curves for the model neurons are shown in the Supplementary Material.
Summary of predictions
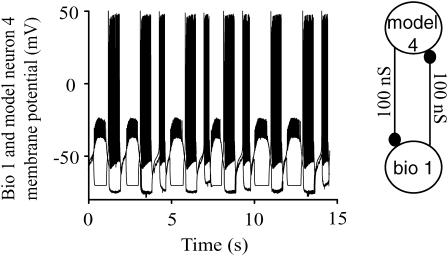
Our intent was to predict which of the 164 distinct circuits created by utilizing different biological neurons reciprocally coupled to different models at varying values of the synaptic conductances in each direction would exhibit stable 1:1 phase locking, and further to predict the actual values of the stimulus and recovery intervals for each neuron as well as the phase-locked period for the circuit. Fig. 4 illustrates the type of firing pattern that one would expect if no stable 1:1 phase locking existed: the period, stimulus intervals, and even firing order are variable since the model neuron often, but not always, fires twice before the biological neuron fires. Table 1 indicates for each model circuit that 1:1 locking was observed by an “a” before the slash and that it was predicted by an “a” after the slash, such that “a/a” indicates a successful prediction. In this table, “c/−” also indicates a success because a complex mode such as that shown in Fig. 4 was observed, and the dash indicates that no 1:1 mode was predicted to exist. The three failures are indicated in bold by “c/a,” which signifies that a complex mode was observed despite a prediction of 1:1 phase locking. In each of these cases, gbio>model was less than or equal to 2 nS, so the difficulty seems to be related to the low value of this parameter. In addition, these were the only cases in which the burst in AB/PD would have been truncated in the predicted mode. We will illustrate the prediction method using two successful specific examples and then summarize the accuracy of our predictions quantitatively.
FIGURE 4.
Example with no stable 1:1 locking mode. In this particular case, a large ratio of the intrinsic periods of 2.5:0.92 for gmodel4>bio1 = 100 nS resulted in a complicated interplay of transient 2:1 and 1:1 locking in the absence of a 1:1 steady phase locking mode. Tall bursts are model neuron bursts; short bursts are biological.
Example of a prediction that did not require consideration of second order resetting
Fig. 5 gives an example of the prediction method using a hybrid circuit with gmodel1>bio4 = 100 nS and gbio4>model1 = 100 nS. The polynomial fit to the average of the first order PRCs (Fig. 5 A1) and to the average total resetting (Fig. 5 A2) were used to compute the dependence of recovery interval on the stimulus interval for both the biological (long dashes) and the model (short dashes) neuron as explained in the Methods, with the contribution of second order resetting ignored in Fig. 5 B1 but considered in Fig. 5 B2. The contribution of second order resetting in the biological neuron is negligible (Fig. 3 A2), but the effect of including the essentially constant second order resetting (triangles pointing up in Fig. 3 B2) of about −0.25 is to shift the linear PRC for the model in a downward direction. It also produces a downward shift of the recovery intervals for the model neuron (short dashes) between Fig. 5, B1 and B2. This shift causes the short dashed graph to appear shortened, because negative (acausal) stimulus intervals were not plotted (see Methods).
FIGURE 5.
Prediction of the phase-locked mode in a hybrid network. (A) The best polynomial fits for the first order (A1) and total (A2) phase resetting for the biological neuron 4 (long dashed line) and model neuron 1 (short dashed line) with both synaptic conductances equal to 100 nS. The phases of each neuron in the phase-locked mode are marked by ▪ on the corresponding PRCs (A1 and A2). (B) The recovery interval for the model neuron (short dashed line in B1 and B2) plotted versus the model neuron stimulus interval, and the recovery interval of the biological neuron plotted versus the biological neuron stimulus interval (long dashed line in B1 and B2), considering the contribution of first order resetting only (B1) and total resetting (B2). The intersection of the two graphs gives the steady values of the stimulus and recovery intervals. (C) Membrane potential recordings from the isolated biological neuron 4 (C1) and model neuron 1 (C2). In these and other traces, the peaks of the action potentials were not always captured due to the sampling rate. The average value of the intrinsic period of oscillation, P0, and the intrinsic burst durations, b0, is shown for each neuron. The dashed horizontal lines indicate the burst threshold. (D) The actual firing pattern observed in the hybrid circuit had recovery intervals and a period similar to that of the predicted stable 1:1 phase-locked mode (for numerical values see text), despite a substantial shortening of the burst duration in the model neuron 1 compared to its intrinsic duration (shaded bar). In contrast, the burst duration of the biological neuron was nearly the same as its intrinsic value (solid bar). The closed loop hybrid circuit is schematically represented next to the membrane potential record.
The intrinsic period of the biological neuron 4 was 1.29 ± 0.05 s (Fig. 5 C1), and the intrinsic period of model neuron 1 was 1.09 s (Fig. 5 C2), and Fig. 5 D shows the 1:1 phase locking that was actually observed when the two were coupled in the hybrid circuit. The predictions using only first order resetting (the intersection point in Fig. 5 B1) were quite accurate, giving a value of 0.651 s for trmodel1, which is a 2% error compared to the average observed value of 0.674 s, and a value of 0.656 s for trbio4, which has a 3% error compared to the average observed value of 0.637 s. Adding these two quantities results in a predicted phase-locked period of Pe = 1.307 s, which has only a 0.4% error compared to the average observed value of 1.312 s. Using the second order PRC contributions to the total phase resetting moved the intersection point only slightly to the left in Fig. 5 B2, resulting in a predicted value of 0.659 s for trmodel1, which gives a 3% error rather than a 2% error, and a predicted value of 0.658 s for trbio4 = 0.658 s (a 2% rather than a 3% error) and an identical prediction for the phase-locked period of 1.317 s. Therefore, for this particular example, the prediction based on both F1 and F2 is not significantly different from the prediction based only on the first order resetting, F1.
The reason for the lack of impact of the contribution of F2 results from the resemblance of the graph of the stimulus versus recovery interval for the model neuron to vertical lines in Fig. 5, B1 and B2. This is a consequence solely of the linear form (Demir et al., 1997; Oprisan et al., 2003; Prinz et al., 2003) of the first order PRC for the model neuron (Fig. 3 B1). The PRC has essentially unit slope (see m1,model in Table 2). Therefore, the first order resetting is equal to the phase minus a constant we can denote ϕ0. Substituting ϕ − ϕ0 for F1(ϕ) in the expression for the recovery interval of the model neuron (see Methods) produces trmodel = P0model (1 − ϕ0), so the x coordinate of the short dashed graph in Fig. 5, B1 and B2, is very nearly constant and independent of the stimulus phase ϕ. On the other hand, the contribution of F2 shifts the y coordinate, the model stimulus interval, downward by ∼250 ms for each recovery interval. The example in the next section shows that although this shift is quantitatively unimportant for the example in Fig. 5, it can be qualitatively very significant if it causes the intersection to appear or disappear entirely.
A close inspection of the actual membrane potential recordings in the phase-locked mode (Fig. 5 D) shows that although the duration of the burst in the biological neuron remained near its intrinsic value of 0.527 s, the model neuron burst duration was 0.12 s during phase-locked mode compared to an intrinsic value of 0.28. We conclude that near the particular phase 0.523 (marked by squares in Fig. 5, A1 and A2) at which the biological neuron receives an input from the model neuron in the hybrid circuit, the phase resetting is not very sensitive to burst duration, and hence the prediction algorithm is very robust in this case to striking changes in burst duration from the open to the closed loop condition. Since insensitivity to burst duration is not always the case (Oprisan et al., 2003; Prinz et al., 2003), this is a potential source of error (see Discussion).
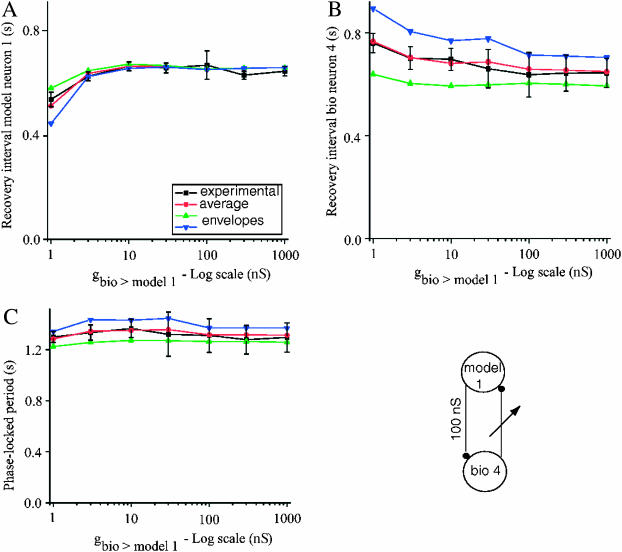
Fig. 6 summarizes the predictions made using the hybrid circuit with gmodel1>bio4 = 100 nS at seven values of gbio4>model1. A shows the recovery interval for the model neuron, B shows the recovery interval for the biological neuron, and C shows their sum, which is the period. The experimentally measured values are given in all panels by black squares connected by black lines. The predictions using the average resetting are given by red circles connected by a red line, and in this case overlay quite well with the experimental data. The predictions based on the upper and lower (triangles on the blue and green curves) envelopes largely bracket the experimental results. Note that the predicted phase-locked period (Fig. 6 C) is always close to the intrinsic period of the biological neuron (1.29 s) at all values of gbio4>model1, suggesting that the flat region in the PRC of the biological neuron (Fig. 5, A1 and A2) may be a globally attracting set of the network dynamics.
FIGURE 6.
Summary of results for a selected group of hybrid circuits comprised of model neuron 1 and biological neuron 4. The experimentally observed values are given by the ▪ (black line), the predicted values using the average PRC by • (red line), and the predictions using the upper and lower envelopes are given by ▴ and ▾ (blue and green lines). (A) Recovery intervals for the model neuron. (B) Recovery intervals for the biological neuron. (C) Phase-locked period. The predictions based on the average PRC are in good agreement with the experimentally measured values (▪), and predictions based on the envelopes generally bracket the range of the experimentally observed values. The closed loop hybrid circuit is schematically represented in the lower right-hand corner.
Thus far, we have illustrated only the portion of the analysis that uses periodicity constraints to predict modes that can exist because they satisfy these constraints. To predict that a mode will be observed, we must also predict that the mode will be stable, and as described in the Methods, the contribution of F2 to the stability criterion can either be considered or ignored. In general, the hybrid circuit did not provide a good test case to determine whether the stability criteria correctly predict the effect of F2, because in general, the slopes of the first order PRCs were between 0 and 1, and the slope of the second order PRC was near 0. These values guarantee stability regardless of whether the contribution of F2 is considered. For the example given in Fig. 5, the entry in Table 2 for gbio4>model1 = 100 nS shows that ignoring F2 gives a multiplier λ equal to zero, whereas considering F2 produces λ1 and λ2 equal to 0.108 and 0.037, all of which have absolute values smaller than 1. Hence both methods predict a stable 1:1 phase-locked mode, as they do for all seven values of gbio4>model1 = 100 nS considered in Fig. 6. The very small values of λ imply that perturbations decay quickly, producing rapid convergence to the limit cycle for the component neurons as required by our assumptions.
Example of a prediction that did require consideration of second order resetting
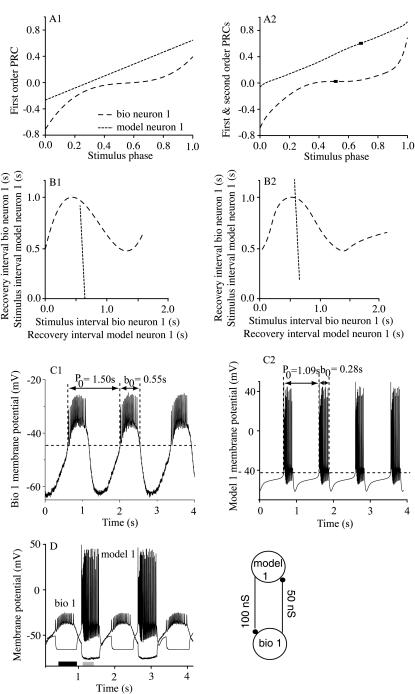
Fig. 7 shows an example of a hybrid circuit in which the consideration of second order resetting was crucial to a correct analysis, the hybrid network formed with the biological neuron 1 and model neuron 1 (gmodel1>bio1 = 100 nS, gbio1>model1 = 50 nS). The first order resetting alone is shown for both the biological (long dashes) and model (short dashes) neuron (Fig. 7 A1). The addition of second order resetting (Fig. 7 A2) produces only a small change in the PRC for the biological neuron, but shifts the PRC for the model neuron upward, corresponding to a constant delay of ∼200 ms, the opposite of what was observed in Fig. 5, A1 and A2. When second order resetting is ignored (Fig. 7 B1), there is no intersection point between the two recovery versus stimulus interval curves of the neurons, and hence no 1:1 mode is predicted to exist. The contribution of F2 to the stimulus interval for the model neuron 1 causes the dotted curve in Fig. 7 B2 to be shifted upward, as explained above, such that an intersection with the curve for the biological neuron 1 does indeed occur. Fig. 7 C1 shows the average intrinsic period of the biological neuron to be 1.5 s and that of the model 1 neuron to be 1.09 s. Fig. 7 D shows the 1:1 phase-locked mode obtained when the circuit was closed. Using the intersection point in Fig. 7 B2 resulted in a predicted value of 0.773 s for trmodel1 compared to an actual average value of 0.776 s, corresponding to a 0.4% error, a predicted value of 0.656 s for trbio1 compared to the actual average value of 0.746 s, corresponding to a 12% error, and a prediction for the phase-locked period of 1.429 s compared to the actual average period of 1.522 s (6% prediction error). A close inspection of the actual membrane potential recordings in the phase-locked mode (Fig. 7 D) shows that although the duration of the burst in the biological neuron remained near its intrinsic value of 0.55 s, the model neuron burst duration was 0.5 s during phase-locked mode compared to an intrinsic value of 0.28 s. The significant increase in the burst duration of the model neuron 1 for this particular hybrid network (gmodel1>bio1 = 100 nS, gbio1>model1 = 50 nS) during the phase-locked mode causes the biological neuron to be released from inhibition at a later time than would be predicted by the intrinsic burst duration, potentially resulting in a longer recovery interval for the biological neuron 1 in closed loop than predicted. This in turn could lead to the observed systematic underestimation of the recovery of the biological neurons, which is evident in the summary in Fig. 8 B. The lack of an intersection that satisfies all periodicity constraints in the absence of consideration of the effects of F2 as shown in Fig. 7 B1 is not unique to this example but rather occurred in 21 out of the 164 tested circuits, including all those listed in Tables 1 and 3 with gbio1>model1 ≥ 10 nS at two values of gmodel1>bio1 (100 nS and 500 nS) and model neuron 5 coupled to biological neuron 1 (gmodel5>bio1 = 100 nS).
FIGURE 7.
Prediction of the phase-locked mode in a hybrid network showing the essential contribution of the second order PRC. (A) The best polynomial fits for the first order (A1) and total (A2) phase resetting for the biological (gmodel1>bio1 = 100 nS, long dashes) and model neuron 1 (gbio1>model1 = 50 nS, short dashes). The second order PRC of the model neuron 1 has a significant positive value that shifts the PRC upward (compare the short dashed curves in A2 and A1). The phases of each neuron in the phase-locked mode are marked by squares on the corresponding PRCs (A2). (B1) There is no intersection between the two recovery versus stimulus interval curves if only the first order resetting is considered. (B2) There is an intersection between the two recovery versus stimulus interval curves if both the first and second order resetting is considered. (C) Membrane potential recordings from (C1) the isolated biological neuron 1 and (C2) the isolated model neuron 1. (D) The actual firing pattern observed in the hybrid circuit had recovery intervals and a period similar to that of the predicted stable 1:1 phase-locked mode (for numerical values see text), despite a substantial lengthening of the burst duration of the model neuron 1 compared to its intrinsic duration (shaded bar in D). The closed loop hybrid circuit is schematically represented in the lower right-hand corner.
FIGURE 8.
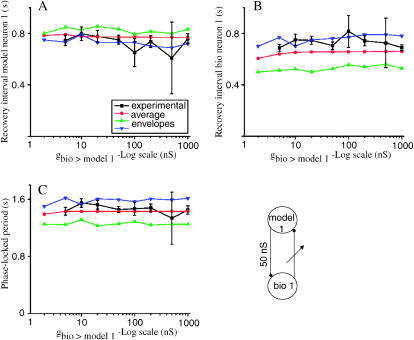
Summary of results for a selected group of hybrid circuits comprised of model neuron 1 and biological neuron 1. The experimentally observed values are given by the ▪ (black line), the predicted values using the average PRC by • (red line), and the predictions using the upper and lower envelopes are given by ▴ and ▾ (blue and green lines). (A) Recovery intervals for the model neuron. (B) Recovery intervals for the biological neuron. (C) Phase-locked period. As in Fig. 6, the predictions based on the envelopes generally bracket the experimentally observed values. The predictions based on the average PRC were used to calculate the error (Table 3). The closed loop hybrid circuit is schematically represented in the lower right-hand corner.
Fig. 8 summarizes the predictions made using the hybrid circuit with gmodel1>bio4 = 100 nS at eight values of gbio1>model1. A shows the recovery interval for the model neuron, B shows the recovery interval for the biological neuron, and C shows their sum, which is the period. The experimentally measured values are given in all panels by black squares connected by black lines. There is no experimental value at gbio1>model1 = 2 nS, because according to the entry in Table 1, a complex mode was observed although 1:1 phase locking was predicted at this value. The predictions using the average resetting are given by red circles connected by red lines, and in this case do not overlay quite as well with the experimental data as the example in Fig. 6, but the discrepancy is still within the variability of the data. The predictions based on the upper and lower (triangles on the blue and green curves) envelopes still largely bracket the experimental results. On average, the recovery interval of the model neuron 1 was overestimated by 8%, whereas the recovery interval of the biological neuron was underestimated by ∼10% (Table 3). The prediction error for the phase-locked period was only ∼5% (see next section). Note that the observed phase-locked period (Fig. 8 C) is again always close to the intrinsic period (1.50 s) of the biological neuron at all values of gbio1>model1.
Quantitative summary of results
Table 3 gives a quantitative summary of the accuracy of the predictions. For each of the 20 combinations of a given model neuron and a given biological neuron at a fixed value of gmodel>bio, we summed the error over all values of gbio>model and reported the statistics. The values for the examples given in Figs. 6 and 8 are shown in bold. The first example (Fig. 6) shows that over a range of seven gbio4>model1, the average error was 1.3 ± 0.8 and −0.3 ± 1.1, respectively, for the biological and model neuron recovery intervals. These numbers are at the lower end of those we observed and reflect the excellent fit shown in Fig. 6, A and B. The error when F2 was not considered was −0.7 ± 1.3 and −2.2 ±1.9, which indicates that the contribution of F2 did not improve (or worsen) our prediction in this case. The other example, given in Fig. 8 over a range of eight values of gbio1>model1 for which phase-locked modes were observed, gives average errors that were at the high end of those observed with the correction for F2 included, −10.2 ± 3.1 and 8.0 ± 3.3, respectively, for the biological and model neuron recovery intervals. In addition, this example illustrates an extreme case in which the existence of 1:1 phase-locked modes could not be predicted without the contribution of F2. The consideration of second order effects was required for the prediction of the observed 1:1 phase locking in a total of three of the combinations (specifically in 21 individual circuits as described above). In several cases, such as for model neuron 7 combined with biological neuron 2 or 4, considering the contribution of F2 drastically reduced the average error in the recovery interval of the biological neuron, whereas in others, such as model neuron 2 or 6 coupled with biological neuron 3, the average error in the recovery interval of the model neuron was drastically reduced. In all but two combinations, the mean prediction error of both recovery intervals was smaller when the contribution of the second order PRC to the total phase resetting was considered. In all but five combinations, the SE of both recovery intervals was smaller when the contribution of the second order PRC was considered.
Although in general this data set did not lend itself to a test of the predictive efficacy of including F2 in the stability criterion, the case of the hybrid network gbio1>model5 = 1 nS and gmodel5>bio1 = 100 nS did provide such a test. The steady phase of the biological neuron in the predicted 1:1 mode was ϕbio1 = 0.754, and the slopes of the PRCs at that phase were m1bio1 = 0.4, m2bio1 = 0.0, m1model5 = −0.733, and m2model5 = 0.263. Based on the first order stability criterion, the absolute value of the characteristic root λ is 1.33, which is greater than 1, so that the steady mode is predicted to be unstable. However, considering the contribution of the second order PRC decreases the maximal value of λ to 0.78, which correctly predicts that the observed 1:1 phase-locked mode will be stable. In a total of 9 out of 164 circuits, stable phase locking would be incorrectly predicted to be unstable if the effects of the second order phase resetting on the stability criterion were not taken into account. This provides further support for the importance of considering the contribution of second order resetting.
If there is an offset between the activation of the coupling with the postsynaptic neuron and the initiation of a burst in the presynaptic neuron, the Methods explain how to implement the periodicity constraints, and an example is included in the Supplementary Material. Such an offset could in principle result from axonal delays or from graded synaptic coupling in which activation of the coupling precedes burst onset. All of the entries in Table 3 corresponding to circuits composed of biological neuron 3 and model neuron 2 were calculated in the presence of such an offset, and the errors were neither excessively high nor low compared to the remainder of the circuits that had no such offset.
In Table 3, the signs of the errors for the recovery interval in the two neurons are frequently opposite. The peculiarities of the specific PRCs utilized, including the flat region in the PRC that is often observed in a range of phase bracketing 0.5 in the biological neuron (Fig. 5 A1, long dashes) and the linearity with unit slope observed in the PRC for the model neuron, frequently combined to produce compensatory errors in the two recovery intervals as follows. In the flat region of the first order PRC for the biological neuron, F1bio(ϕ) = φ0 = constant, thus trbio = P0bio (1 − ϕ + φ0), which produces a region of negative unit slope in the curve indicated by dashes in Figs. 5 and 7, B1 and B2. Since the slope of the biological neuron recovery interval curve near the intersection point is −1, and the model recovery interval resembles a straight vertical line, a shift in the model recovery interval produces an equal and opposite shift in the recovery interval for the biological neuron and leaves the prediction of the period essentially constant in the region of negative unit slope in the recovery interval curve produced by the flat region in the first order PRC for the biological neuron. Additional examples of this phenomenon are given in the Supplementary Material.
DISCUSSION
Validity of the mathematical analysis
Mathematical biology requires that assumptions be made to map the mathematics onto aspects of the biological system under study. These assumptions always involve an approximation, and the validity of the mathematical model in a given situation depends upon the quality of the approximation. Most previous theoretical work on the phase-locked modes in biological oscillators has focused on weakly coupled, simple integrate and fire (IF) neurons (Hansel et al., 1995; Mirollo and Strogatz, 1990; van Vreeswijk et al., 1994), IF neurons with arbitrarily strong pulse coupling (Bressloff and Coombes, 1998), spike response methods applied to neurons with standard dynamics, i.e., to IF and type I neurons (Gerstner et al., 1996), or spiking neurons with negligible second order resetting (Goel and Ermentrout, 2002). These studies are all based on assumptions that are inappropriate for the bursting neurons, strong coupling, and relaxation oscillator dynamics observed in the hybrid circuits in this study.
The mathematical model that we present is a discrete, cycle-by-cycle mapping of the activity of two coupled neurons in the hybrid circuit that requires no knowledge of the equations governing the dynamics of each neuron, only the empirically determined PRC. The following essential assumptions were made in this study: 1), the complex composed of the soma and extended neuritic trees of both PD neurons and the AB neuron to which they are electrically coupled can be represented by a single, lumped oscillator termed the biological neuron, 2), both the biological neuron and the model neuron in the circuit are noiseless limit cycle oscillators, 3), each neuron either returns close to its original unperturbed limit cycle before the next input is received or if the cycle period changes over time, it returns to a limit cycle identical to the original one remapped to the new cycle period, and 4), the input received by each neuron has the same effect in the closed loop circuit as in the open loop circuit used to generate the phase resetting. The accuracy of the results was satisfactory for 161 of the 164 circuits (see Table 1), was quite good in many cases (see Fig. 6), and in almost every case was within the 10% variability in the period of the biological neurons. To fully understand the approximations that are introduced by the assumption, and to demonstrate where vigilance is required by others attempting to implement similar methods, we elaborate below on violations of the assumptions and their potential consequences.
The first assumption regarding the lumped AB/PD oscillator kernel was violated in several instances but fortuitously did not affect the accuracy of our predictions. In some cases, a pulse that effectively hyperpolarized the PD neuron from which we were recording did not terminate an ongoing burst, complete with spikes, presumably occurring elsewhere in the AB/PD complex due to insufficient space clamp (Fig. 9 A). In another case, a perturbation applied around a phase of 0.75 had variable results, producing an apparent discontinuity in the PRC at that phase. Some trials resulted in a missed cycle in which an attenuated subthreshold depolarization without spikes was initiated during the perturbation instead of a burst (Fig. 9 B), and on other trials no depolarization occurred until after the inhibition (Fig. 9 C). The missed cycle produced an unusually long delay compared to cases in which a rebound burst was observed just after PD was released from inhibition and hence the discontinuity in the PRC (Fig. 9 D). We theorize that no errors were introduced into our analysis by these violations of the assumption because the observed phase locking usually occurs near the middle of the AB/PD cycle, when the input conductance is low and hyperpolarization may propagate more effectively to the oscillator kernel, presumably located in the neurites of the AB neuron.
FIGURE 9.
The AB/PD group could not always be characterized as a single oscillator due to space clamp problems. (A) A burst continued in the oscillator kernel during hyperpolarization of the PD neuron. (B) A hyperpolarizing stimulus applied at a phase of 0.75 either (B) prevented a burst from occurring until the hyperpolarizing current was terminated, resulting in a short delay, or (C) attenuated the burst, resulting in a missed cycle and long delay. (D) The PRC for biological neuron 2 under these conditions exhibited a spurious discontinuity near a phase of 0.75 in which the upper branch corresponded to C and the lower to B.
The second assumption was more problematic, and the approximation introduced herein is likely responsible for the bulk of the numeric errors. One source of error is hardware dependent: the dynamic clamp can introduce numerical error since the setup used has an average integration time step of ∼0.06 ms, but individual time steps have variable lengths around that value. Some variability was observed in the duty cycle of the model neurons in some simulations as a result of numerical errors; yet interestingly, much less variability was observed in the period. The biological neuron was a more significant source of error, and a conclusion of this study is that the method can, at least in some cases, tolerate levels of noise present in real biological systems. The major sources of noise in the biological portion of the experimental setup were the trial-to-trial variability inherent in the experimental determination of the PRC due to noise and fluctuations in the modulatory state of the biological circuit and the cycle-to-cycle variability of the period. Since a constant intrinsic period is assumed to calculate both the phases at which perturbations are applied and the resultant normalized delay or advance that results from the perturbation, the cycle-to-cycle variability in the period is likely to be responsible for much of the trial-to-trial variability in the PRC. In the experimental setup described in this article, the pyloric pacemaker still receives many modulatory inputs from anterior ganglia in the stomatogastric nervous system. In addition, gastric mill events can cause a transient change in the period of the pyloric pacemaker (Bartos and Nusbaum, 1997; Bartos et al., 1999; Marder et al., 1998; Mulloney, 1997; Nadim et al., 1998, 1999; Thuma and Hooper, 2002). In many cases, due to long-term trends, the period of the biological neuron immediately before the coupling in the hybrid circuit was turned on was different than when the PRC was measured. To utilize the PRC determined using a different intrinsic period to make predictions for that hybrid circuit, we were forced to make the additional assumption that the limit cycle with the new period is identical to the original one remapped to the new cycle period. This assumption guarantees a constant duty cycle, but there is insufficient evidence to support any particular mapping of the phase as cycle period is varied. The impact of the trial-to-trial variability of the PRC was addressed by using the average PRC for the predictions but also by comparing the spread of the predictions resulting from using the upper and lower envelopes of the experimental PRCs. We concluded that the trial-to-trial variability could account for much of the observed errors. The cycle-to-cycle variability of the period was 10%, and the predictions of the average period fell within that range.
The third assumption regarding the return to the limit cycle before receipt of the next input is required for the PRCs obtained at specific phases along the limit cycle in the open loop configuration to apply in the closed loop. Potential violations of this assumption could be introduced in at least two ways: higher order PRCs in response to a single pulse and temporal summation of slow processes in response to a train of pulses. In the first scenario, the deviation from the limit cycle produced by a single pulse does not die out within one trip around the limit cycle. F1 measures the portion of the resetting that occurs during one cycle before the next burst, and F2 presumably measures the resetting that occurs after burst initiation but still before the returning to the original point on the limit cycle at which the perturbation was received. If higher order PRCs are not negligible, then errors are introduced by the application of the open loop PRC because the phase cannot be precisely determined unless the trajectory is very near the original limit cycle. The manner in which F2 is tabulated does not guarantee that all of the resetting occurs before a return to the original phase. Furthermore, in some hybrid networks, such as biological neuron 3 coupled with model neuron 2 (data not shown), the third order PRCs are not negligible, and could be responsible for the observed systematic errors. In this hybrid circuit the duration of the perturbation is very long compared to the cycle period in the model, so the assumption of pulsatile coupling could be violated because the trajectory cannot return to the limit cycle during the interburst. The burst duration in model neuron 3 is 1.06 s, which is 84% of the 1.26-s intrinsic period of biological neuron 2 before coupling with model neuron 3 (see Supplementary Material for an example). Although the mean prediction error of the recovery interval for this circuit was small (0.6%), the SE (9.2%, Table 3) is a better indicator of prediction accuracy. A second, distinct source of error could result if a single perturbation causes a small deviation from the limit cycle, but repeated, periodic applications of the perturbation cause the trajectory to move farther away from the limit cycle such that the distance summates temporally. In this manner, the presence of slow conductances could result in systematic errors.
The final assumption is that the input received by each neuron has the same effect in the closed loop circuit as in the open loop circuit used to generate the phase resetting. This does not require the burst to be identical in both cases, because in some instances the phase resetting can be insensitive to duration at the phase locked point (Oprisan et al., 2003), but a change in burst duration can also be an important source of error. For some model neurons, the duration of the first burst (see Fig. 1 D) after the perturbation is applied can differ from its intrinsic value measured in the open loop setup, and Figs. 5 D and 7 D show that the duration of the burst in the model neuron differs in the open and closed loop conditions. Thus, violation of this final assumption is a potentially important source of error, although in this article the errors introduced were not excessively large in magnitude (see Supplementary Material).
Applications to CPGs and other phase-locked circuits
An interesting feature of certain CPGs is that the characteristic pattern is preserved over a large range of frequencies (phase constancy; see Hooper, 1997). The promise of our methodology is that it may provide insight both into how the pattern is maintained and the circumstances that cause it to break down, such as a change in the slope of the first or second order PRC that renders the mode unstable, or a change in the magnitude of the PRC that makes it impossible for the periodicity constraints to be satisfied. Fig. 7 provides an excellent illustration of how a change in the second order resetting, for example, can cause a phase-locked mode to appear or disappear. In addition, to our knowledge, no other analysis of the existence or stability of phase locking in neural circuits has considered the effects on the second cycle after a perturbation is received. As we have shown here, such effects are particularly important for bursting neurons. However, pyramidal neocortical neurons have been shown to exhibit second order resetting as a result of a depolarizing pulse (Reyes and Fetz, 1993); therefore, theories of phase locking in cortical networks may also need to include the effects of F2. The robustness of our methods to the presence of delays is also noteworthy.
SUMMARY
In this study, we successfully applied theoretical methods that had previously only been tested on models (Canavier et al., 1997, 1999; Luo et al., 2004) to a hybrid circuit composed of a model neuron and a biological neuron connected via artificial synapses implemented with the dynamic clamp. This resulted in a large measure of control over the experimental setup, although nonetheless allowing for the rich variability and complexity inherent in physiological neurons, and established the applicability of the theoretical methods to this circuit. The reason that we emphasize the accuracy of our predictions is simply to provide a level of confidence in the proposed framework for understanding the basis for the generation of a particular rhythmic oscillatory pattern. The pyloric circuit may be one of the more severe tests of our conceptual framework with respect to noisy operation; a recent editorial (Hooper, 2004) argues that motor pattern generating networks involved in feeding are more likely to exhibit and even benefit from cycle-to-cycle variability than circuits that mediate behaviors in which such variability confers no advantage, as in swimming or flying, or even introduces a prohibitive cost of failure, as in terrestrial locomotion. Thus the degree of accuracy attained by our predictive method applied to a hybrid circuit containing the pacemaker of the pyloric circuit bodes well for its applicability to other biological circuits.
SUPPLEMENTARY MATERIAL
An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.
Supplementary Material
Acknowledgments
The authors thank Dr. Eve Marder for her support and for her comments on an earlier draft of the manuscript.
This research was supported by National Institutes of Health MH-46742 (Eve Marder) and National Science Foundation IBN-0118117 (C.C.C.) grants.
References
- Acker, C. D., N. Kopell, and J. A. White. 2003. Synchronization of strongly coupled excitatory neurons: relating network behavior to biophysics. J. Comput. Neurosci. 15:71–90. [DOI] [PubMed] [Google Scholar]
- Arshavsky, Yu. I., T. G. Deliagina, G. N. Orlovsky, and Yu. V. Panchin. 1989. Control of feeding movements in the pteropod mollusc, Clione limacina. Exp. Brain Res. 78:387–397. [DOI] [PubMed] [Google Scholar]
- Arshavsky, Yu. I., S. Grillner, G. N. Orlovsky, and Yu. V. Panchin. 1991. Central generators and the spatiotemporal pattern of movements. In The Development of Timing Control. J. Fagard and P. H. Wolff, editors. Elsevier, Amsterdam, The Netherlands. 93–115.
- Bal, T., F. Nagy, and M. Moulins. 1988. The pyloric central pattern generator in crustacea: a set of conditional neuronal oscillators. J. Comp. Physiol. 163:715–727. [Google Scholar]
- Bartos, M., Y. Manor, F. Nadim, E. Marder, and M. P. Nusbaum. 1999. Coordination of fast and slow rhythmic neuronal circuits. J. Neurosci. 19:6650–6660. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bartos, M., and M. P. Nusbaum. 1997. Intercircuit control of motor pattern modulation by presynaptic inhibition. J. Neurosci. 17:2247–2256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bressloff, P. C., and S. Coombes. 1998. Desynchronization, mode locking, and bursting in strongly coupled integrate-and-fire oscillators. Phys. Rev. Lett. 81:2168–2171. [Google Scholar]
- Canavier, C. C., D. A. Baxter, J. W. Clark, and J. H. Byrne. 1999. Control of multistability in ring circuits of oscillators. Biol. Cybern. 80:87–102. [DOI] [PubMed] [Google Scholar]
- Canavier, C. C., R. J. Butera, R. O. Dror, D. A. Baxter, J. W. Clark, and J. H. Byrne. 1997. Phase response characteristics of model neurons determine which patterns are expressed in a ring circuit model of gait generator. Biol. Cybern. 77:367–380. [DOI] [PubMed] [Google Scholar]
- Demir, S. S., R. J. Butera, A. A. DeFranceschi, J. W. Clark, and J. H. Byrne. 1997. Phase sensitivity and entrainment in a modeled bursting neuron. Biophys. J. 72:579–594. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dror, R., C. C. Canavier, R. J. Butera, J. W. Clark, and J. H. Byrne. 1999. A mathematical criterion based on phase response curves for stability in a ring of coupled oscillators. Biol. Cybern. 80:11–23. [DOI] [PubMed] [Google Scholar]
- Ermentrout, G. B. 1996. Type I membranes, phase resetting curves, and synchrony. Neural Comput. 8:979–1001. [DOI] [PubMed] [Google Scholar]
- Gerstner, W., J. L. van Hemmen, and J. D. Cowan. 1996. What matters in neuronal locking. Neural Comput. 8:1653–1676. [DOI] [PubMed] [Google Scholar]
- Glass, L., and M. Mackey. 1988. From Clocks to Chaos, the Rhythms of Life. Princeton University Press, Princeton, NJ.
- Goel, P., and G. B. Ermentrout. 2002. Synchrony, stability, and firing patterns in pulse-coupled oscillators. Physica D. 163:191–216. [Google Scholar]
- Goldman, M. S., J. Golowasch, E. Marder, and L. F. Abbott. 2001. Global structure, robustness, and modulation of neuronal models. J. Neurosci. 21:5229–5238. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hansel, D., G. Mato, and C. Meunier. 1995. Synchrony in excitatory neural networks. Neural Comput. 7:307–337. [DOI] [PubMed] [Google Scholar]
- Harris-Warrick, R. M., E. Marder, A. I. Selverston, and M. Moulins. 1992. Dynamic Biological Networks. The Stomatogastric Nervous System. MIT Press, Cambridge, MA.
- Hartline, D. K. 1979. Pattern generation in the lobster (Panulirus) stomatogastric ganglion. II. Pyloric network simulation. Biol. Cybern. 33:223–236. [DOI] [PubMed] [Google Scholar]
- Hartline, D. K., and D. V. Gassie. 1979. Pattern generation in the lobster (Panulirus) stomatogastric ganglion. I. Pyloric neuron kinetics and synaptic interactions. Biol. Cybern. 33:209–222. [DOI] [PubMed] [Google Scholar]
- Hooper, S. L. 1997. Phase maintenance in the pyloric pattern of the lobster (Panulirus interruptus) stomatogastric ganglion. J. Comput. Neurosci. 4:191–205. [DOI] [PubMed] [Google Scholar]
- Hooper, S. L. 2004. Variation is the spice of life. Focus on “cycle-to-cycle variability of neuromuscular activity in Aplysia feeding behavior”. J. Neurophysiol. 92:40–41. [DOI] [PubMed] [Google Scholar]
- Hoppensteadt, F. C., and E. M. Izhikevich. 1997. Weakly Connected Neural Networks. Springer-Verlag, New York.
- Kopell, N., and G. B. Ermentrout. 1988. Coupled oscillators and the design of central pattern generators. Math. Biosci. 90:87–109. [Google Scholar]
- Liu, Z., J. Golowasch, E. Marder, and L. F. Abbott. 1998. A model neuron with activity-dependent conductances regulated by multiple calcium sensors. J. Neurosci. 18:2309–2320. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luo, C., C. C. Canavier, D. A. Baxter, J. H. Byrne, and J. W. Clark. 2004. Multimodal behavior in a four neuron ring circuit: modes switching. IEEE Trans. Biomed. Eng. 51:205–218. [DOI] [PubMed] [Google Scholar]
- Marder, E. 1998. From biophysics to models of network function. Annu. Rev. Neurosci. 21:25–45. [DOI] [PubMed] [Google Scholar]
- Marder, E., and R. L. Calabrese. 1996. Principles of Rhythmic Motor Pattern Generation. Physiol. Rev. 76:687–717. [DOI] [PubMed] [Google Scholar]
- Marder, E., Y. Manor, F. Nadim, M. Bartos, and M. P. Nusbaum. 1998. Frequency control of a slow oscillatory network by a fast rhythmic input: pyloric to gastric mill interactions in the crab stomatogastric nervous system. Ann. N. Y. Acad. Sci. 860:226–238. [DOI] [PubMed] [Google Scholar]
- Miller, J. P., and A. I. Selverston. 1982. Mechanism underlying pattern generation in lobster stomatogastric ganglion as determined by selective inactivation of identified neurons. II. Oscillatory properties of pyloric neurons. J. Neurophysiol. 48:1378–1391. [DOI] [PubMed] [Google Scholar]
- Mirollo, R. M., and S. H. Strogatz. 1990. Synchronization of pulse-coupled biological oscillators. SIAM J. Appl. Math. 50:1645–1662. [Google Scholar]
- Mulloney, B. 1977. Organization of the stomatogastric ganglion of the spiny lobster. V. Coordination of the gastric and pyloric systems. J. Comp. Physiol. 122:227–240. [Google Scholar]
- Nadim, F., Y. Manor, N. Kopell, and E. Marder. 1999. Synaptic depression creates a switch that controls the frequency of an oscillatory circuit. Proc. Natl. Acad. Sci. USA. 96:8206–8211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nadim, F., Y. Manor, M. P. Nusbaum, and E. Marder. 1998. Frequency regulation of a slow rhythm by a fast periodic input. J. Neurosci. 18:5053–5067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oprisan, S. A., and C. C. Canavier. 2001. Stability analysis of rings of pulse-coupled oscillators: the effect of phase resetting in the second cycle after the pulse is important at synchrony and for long pulses. Diff. Eqs. Dyn. Sys. 9:243–258. [Google Scholar]
- Oprisan, S. A., V. Thirumalai, and C. C. Canavier. 2003. Dynamics from a time series: can we extract the phase resetting curve from a time series? Biophys. J. 84:2919–2928. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Panchin, Y. V., Y. I. Arshavsky, A. I. Selverston, and T. A. Cleland. 1993. Lobster stomatogastric neurons in primary culture. I. Basic characteristics. J. Neurophysiol. 69:1976–1992. [DOI] [PubMed] [Google Scholar]
- Perkel, D. H., J. H. Schulman, T. H. Bullock, G. P. Moore, and J. P. Segundo. 1964. Pacemaker neurons: effects of regularly spaced synaptic input. Science. 145:61–63. [DOI] [PubMed] [Google Scholar]
- Pinto, R. D., R. C. Elson, A. Szucs, M. I. Rabinovich, A. I. Selverston, and H. D. Abarbanel. 2001. Extended dynamic clamp: controlling up to four neurons using a single desktop computer and interface. J. Neurosci. Methods. 108:39–48. [DOI] [PubMed] [Google Scholar]
- Pinto, R. D., P. Varona, A. R. Volkovskii, A. Szucs, H. D. I. Abarbanel, and M. I. Rabinovich. 2000. Synchronous behavior of two coupled electronic neurons. Phys. Rev. E. 62:2644–2656. [DOI] [PubMed] [Google Scholar]
- Prinz, A. A., V. Thirumalai, and E. Marder. 2003. The functional consequences of changes in the strength and duration of synaptic inputs to oscillatory neurons. J. Neurosci. 23:943–954. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reyes, A. D., and E. E. Fetz. 1993. Two modes of interspike interval shortening by brief transient depolarizations in cat neocortical neurons. J. Neurophysiol. 69:1661–1672. [DOI] [PubMed] [Google Scholar]
- Selverston, A. I., and M. Moulins. 1987. The Crustacean Stomatogastric System. Springer-Verlag, Berlin.
- Sharp, A. A., M. B. O'Neil, L. F. Abbott, and E. Marder. 1993a. The dynamic clamp: artificial conductances in biological neurons. Trends Neurosci. 16:389–394. [DOI] [PubMed] [Google Scholar]
- Sharp, A. A., M. B. O'Neil, L. F. Abbott, and E. Marder. 1993b. Dynamic clamp: computer-generated conductances in real neurons. J. Neurophysiol. 69:992–995. [DOI] [PubMed] [Google Scholar]
- Tasaki, K., and I. M. Cooke. 1990. Characterization of Ca current underlying burst formation in lobster cardiac ganglion motoneurons. J. Neurophysiol. 63:370–384. [DOI] [PubMed] [Google Scholar]
- Thirumalai, V. 2002. Implications of cotransmission and neuromodulation for neural network function. PhD thesis. Brandeis University, Waltham, MA.
- Thuma, J. B., and S. L. Hooper. 2002. Quantification of gastric mill network effects on a movement related parameter of pyloric network output in the lobster. J. Neurophysiol. 87:2372–2384. [DOI] [PubMed] [Google Scholar]
- Turrigiano, G. G., G. LeMasson, and E. Marder. 1995. Selective regulation of current densities underlies spontaneous changes in the activity of cultured neurons. J. Neurosci. 15:3640–3652. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Vreeswijk, C., L. F. Abbott, and G. B. Ermentrout. 1994. When inhibition, not excitation synchronizes neural firing. J. Comput. Neurosci. 1:313–321. [DOI] [PubMed] [Google Scholar]
- Weaver, A. L., and S. L. Hooper. 2003. Follower neurons in lobster (Panulirus interruptus) pyloric network neurons that regulate pacemaker period in complementary ways. J. Neurophysiol. 89:1327–1338. [DOI] [PubMed] [Google Scholar]
- Winfree, A. T. 1987. The Timing of Biological Clocks. Scientific American Books, New York.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.