Quantum measurement

Idea

Quantum measurement is measurement in quantum mechanics.

The “projection postulate” of quantum physics asserts (von Neumann 1932; Lüders 1951) that:

1. measurement of quantum states is with respect to a choice of orthonormal linear basis $\big\{\vert \psi_b \rangle \big\}_{b : B}$ of the given Hilbert space $\mathscr{H}$ of pure quantum states;

2. the result of measurement on pure quantum states $\vert \psi \rangle \;\in\; \mathscr{H}$ is

   1. a random value $b \in B$;

   2. the “collapse” of the quantum state being measured by orthogonal projection to the linear span of the $b$th basis state.

      $$\array{ P_b &\colon& \mathscr{H} &\xrightarrow{\phantom{---}}& \mathscr{H}_b \hookrightarrow \mathscr{H} \\ && \vert \psi \rangle &\mapsto& P_b \vert \psi \rangle \mathrlap{ = \vert \psi_b \rangle \langle \psi_b \vert \psi \rangle } }$$

In terms of mixed quantum states represented by density matrices, this prescription translates into a quantum operation which is given by a positive-operator valued measure (this is what Lüders (1951) first wrote down).

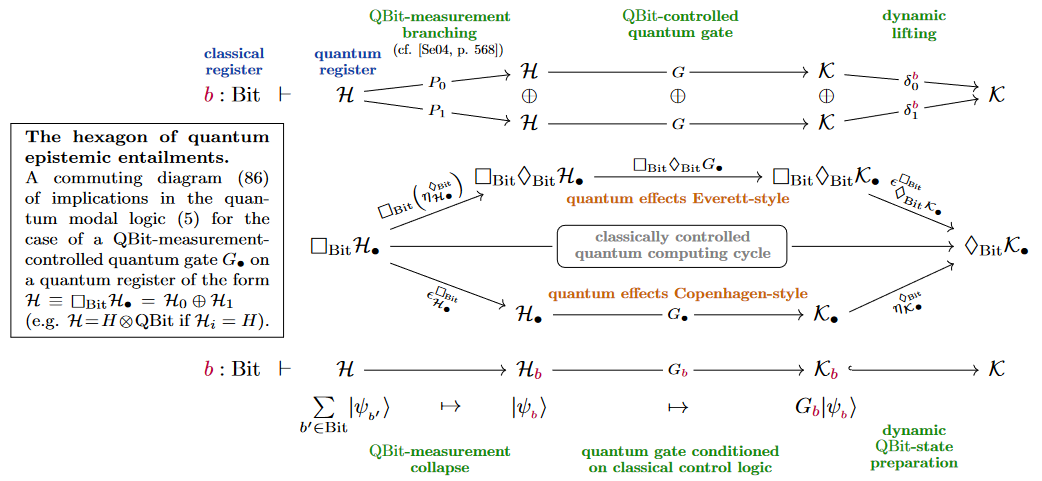
There are different ways to type the quantum measurement, taking into account the non-deterministic nature of its outcome:

1. Regarding the direct sum $\bigoplus_{b \colon B} \mathscr{H}$ of Hilbert spaces as the logical disjunction (“or”) of quantum logic, one may regard measurement as being the linear map into the direct sum whose $b$th component is $P_b$.

   This choice of typing appears (briefly) in Selinger 2004, p. 39, in a precursor discussion that led to the formulation of the quantum programming language Quipper.

2. Regarding the measurement outcome $b \in B$ as the observed context of the actual quantum collapse, one may regard the collapse projection as dependently typed.

   Getting from previous option back to this one is known in the the Quipper-community as dynamic lifting (namely “of the measured bits back into the context”)

\begin{imagefromfile} “file_name”: “PossibleTypingsOfQuantumMeasurement-221025.jpg”, “width”: “560”, “unit”: “px”, “margin”: { “top”: -20, “bottom”: 20, “right”: 0, “left”: 10 } \end{imagefromfile}

Both of these options naturally emerge and are naturally unified in the “Quantum Modal Logic” inherent to dependent linear type theory: This is discussed at quantum circuits via dependent linear types.

Properties

• collapse of the wavefunction

• deferred measurement principle

\linebreak

The “measurement problem”

In the context of interpretation of quantum mechanics it is common to speak of the “measurement problem” when referring to the tension between regarding quantum physics as a probabilistic theory and the idea of realism.

Namely – by the above – a quantum measurement is formally reflected in a change of probabilities. But since in any given measurement experiment one definite outcome is observed, one may wonder how that particular outcome was actually chosen, given that the theory only gives its probability.

(…)

Related concepts

• quantum measurement channel

• deferred measurement principle

• measurement-based quantum computation

• Bell's inequality

• open quantum system

• decoherence

• quantum sensing

• no-cloning theorem

• quantum reader monad

• quantum state preparation

• quantum fluctuation

• quantum probability

• interpretation of quantum mechanics

• mutually unbiased bases

References

General

The original axiomatization of quantum measurement via the projection postulate:

• John von Neumann, §III.3, §V.1 and §VI of:

  Mathematische Grundlagen der Quantenmechanik (German) (1932, 1971) [[doi:10.1007/978-3-642-96048-2](https://link.springer.com/book/10.1007/978-3-642-96048-2)]

  Mathematical Foundations of Quantum Mechanics Princeton University Press (1955) [[doi:10.1515/9781400889921](https://doi.org/10.1515/9781400889921), Wikipedia entry]

• Gerhart Lüders:

  Über die Zustandsänderung durch den Meßprozeß, Ann. Phys. 8 (1951) 322–328 [[doi:10.1002/andp.19504430510](https://doi.org/10.1002/andp.19504430510)]

  Concerning the state-change due to the measurement process, Ann. Phys. 15 9 (2006) 663-670 [[pdf](http://myweb.rz.uni-augsburg.de/~eckern/adp/history/historic-papers/2006_518_663-670.pdf), pdf]

Review and discussion:

• Erhard Scheibe, §VI of: The logical analysis of quantum mechanics, Pergamon Press, Oxford (1973)

• Roland Omnès, §8 of: The Interpretation of Quantum Mechanics, Princeton University Press (1994) [[ISBN:9780691036694](http://press.princeton.edu/titles/5525.html)]

  (with an eye towards interpretations of quantum mechanics)

• Heinz-Peter Breuer, Francesco Petruccione, §2.4 and Part V in: The Theory of Open Quantum Systems, Oxford University Press (2007) [[doi:10.1093/acprof:oso/9780199213900.001.0001](https://doi.org/10.1093/acprof:oso/9780199213900.001.0001)]

  (form the perspective of open quantum systems and with focus on relativistic field theory)

• Joseph M. Renes, §A of: Quantum Information Theory (2015) [[pdf](https://edu.itp.phys.ethz.ch/hs15/QIT/renes_lecture_notes14.pdf)] De Gruyter (2022) [[doi:10.1515/9783110570250](https://doi.org/10.1515/9783110570250)]

• Klaas Landsman, Section 11: of Foundations of quantum theory – From classical concepts to Operator algebras, Springer Open 2017 (doi:10.1007/978-3-319-51777-3, pdf)

In view of dynamical quantum decoherence:

• Maximilian Schlosshauer, Decoherence, the measurement problem, and interpretations of quantum mechanics, Rev. Mod. Phys. 76 (2004) 1267-1305 [[arXiv:quant-ph/0312059](https://arxiv.org/abs/quant-ph/0312059), doi:10.1103/RevModPhys.76.1267]

See also:

• Jürg Fröhlich, Zhou Gang, On the Evolution of States in a Quantum-Mechanical Model of Experiments [[arXiv:2212.02599](https://arxiv.org/abs/2212.02599)]

Discussion in the refined context of (local algebraic) quantum field theory on Lorentzian manifolds:

• Christopher J. Fewster, Rainer Verch, Measurement in Quantum Field Theory [[arXiv:2304.13356](https://arxiv.org/abs/2304.13356)]

Formalization

Brief mentioning of typing and categorical semantics of quantum measurement

in quantum lambda-calculus:

• Peter Selinger, Benoît Valiron, p. 143 of: Quantum Lambda Calculus, Semantic Techniques in Quantum Computation, Cambridge University Press (2009) 135-172 [[doi:10.1017/CBO9781139193313.005](https://doi.org/10.1017/CBO9781139193313.005), pdf]

in the quantum programming language QPL/Quipper:

• Peter Selinger, p. 39 of: Towards a quantum programming language, Mathematical Structures in Computer Science 14 4 (2004) 527–586 [[doi:10.1017/S0960129504004256](https://doi.org/10.1017/S0960129504004256), pdf, web]

Discussion of quantum measurements in terms of quantum information theory via dagger-compact categories, by Frobenius algebra-structures and the quantum reader monad:

• Bob Coecke, Duško Pavlović, Quantum measurements without sums, in: Louis Kauffman, Samuel Lomonaco (eds.), Mathematics of Quantum Computation and Quantum Technology, Taylor & Francis (2008) 559-596 [[arXiv:quant-ph/0608035](https://arxiv.org/abs/quant-ph/0608035), doi:10.1201/9781584889007]

• Bob Coecke, Eric Oliver Paquette, POVMs and Naimark’s theorem without sums, Electronic Notes in Theoretical Computer Science 210 (2008) 15-31 [[arXiv:quant-ph/0608072](https://arxiv.org/abs/quant-ph/0608072), doi:10.1016/j.entcs.2008.04.015]

• Bob Coecke, Eric Paquette, Duško Pavlović, Classical and quantum structures (2008) [[pdf](http://www.comlab.ox.ac.uk/files/627/RR-08-02.pdf), pdf]

• Bob Coecke, Eric Oliver Paquette, Duško Pavlović, Classical and quantum structuralism, in: Semantic Techniques in Quantum Computation, Cambridge University Press (2009) 29-69 [[arXiv:0904.1997](https://arxiv.org/abs/0904.1997), doi:10.1017/CBO9781139193313.003]

• Bob Coecke, Duško Pavlović, Jamie Vicary, A new description of orthogonal bases, Mathematical Structures in Computer Science 23 3 (2012) 555- 567 [[arXiv:0810.0812](https://arxiv.org/abs/0810.0812), doi:10.1017/S0960129512000047]

• Chris Heunen, Martti Karvonen, Exp. 6.5 in: Monads on dagger categories, Theory and Applications of Categories 31 35 (2016) 1016-1043 [[arXiv:1602.04324](https://arxiv.org/abs/1602.04324), TAC:31-35]

and the evolution of the “classical structures”-monad into the “spider”-diagrams (terminology for special Frobenius normal form, originating in Coecke & Paquette 2008, p. 6, Coecke & Duncan 2008, Thm. 1) of the ZX-calculus:

• Bob Coecke, Ross Duncan, §3 in: Interacting Quantum Observables, in Automata, Languages and Programming. ICALP 2008, Lecture Notes in Computer Science 5126, Springer (2008) [[doi:10.1007/978-3-540-70583-3_25](https://doi.org/10.1007/978-3-540-70583-3_25)]

• Aleks Kissinger, §§2 in: Graph Rewrite Systems for Classical Structures in $\dagger$-Symmetric Monoidal Categories, MSc thesis, Oxford (2008) [[pdf](https://www.cs.ox.ac.uk/people/bob.coecke/Aleks.pdf), pdf]

• Aleks Kissinger, §4 in: Exploring a Quantum Theory with Graph Rewriting and Computer Algebra, in: Intelligent Computer Mathematics. CICM 2009, Lecture Notes in Computer Science 5625 (2009) 90-105 [[doi:10.1007/978-3-642-02614-0_12](https://doi.org/10.1007/978-3-642-02614-0_12)]

• Bob Coecke, Ross Duncan, Def. 6.4 in: Interacting Quantum Observables: Categorical Algebra and Diagrammatics, New J. Phys. 13 (2011) 043016 [[arXiv:0906.4725](http://arxiv.org/abs/0906.4725), doi:10.1088/1367-2630/13/4/043016]

Textbook account (though without mentioning the monad structure) in:

• Chris Heunen, Jamie Vicary, around Lem. 5.61 of: Categories for Quantum Theory, Oxford University Press (2019) [[ISBN:9780198739616](https://global.oup.com/academic/product/categories-for-quantum-theory-9780198739616)]

Generalization to Hilbert bundles:

• Chris Heunen, Manuel L. Reyes?, Frobenius Structures Over Hilbert $C^\ast$-Modules, Commun. Math. Phys. 361 (2018) 787–824 [[doi:10.1007/s00220-018-3166-0](https://doi.org/10.1007/s00220-018-3166-0), arXiv:1704.05725]

The Measurement Problem

The article

• Klaas Landsman, Robin Reuvers, A Flea on Schrödinger’s Cat, Found. Phys. 43, 373-407 (2013) (arXiv:1210.2353, pdf)

points out that for symmetric systems with a symmetric ground state, already a tiny perturbation mixing the ground state with the first excited state causes spontaneous symmetry breaking in a suitable limit, and suggests that this already resolves the measurement problem.

See also

• David Wallace, The Quantum Measurement Problem: State of Play (arXiv:0712.0149)