Reducing Cumulative Errors of Incremental CP Decomposition in Dynamic Online Social Networks Reducing Cumulative Errors of Incremental CP Decomposition in Dynamic OSNs
ACM Trans. Knowl. Discov. Data, Vol. 15, No. 3, Article 42, Publication date: April 2021.
DOI: https://doi.org/10.1145/3441645
CANDECOMP/PARAFAC (CP) decomposition is widely used in various online social network (OSN) applications. However, it is inefficient when dealing with massive and incremental data. Some incremental CP decomposition (ICP) methods have been proposed to improve the efficiency and process evolving data, by updating decomposition results according to the newly added data. The ICP methods are efficient, but inaccurate because of serious error accumulation caused by approximation in the incremental updating. To promote the wide use of ICP, we strive to reduce its cumulative errors while keeping high efficiency. We first differentiate all possible errors in ICP into two types: the cumulative reconstruction error and the prediction error. Next, we formulate two optimization problems for reducing the two errors. Then, we propose several restarting strategies to address the two problems. Finally, we test the effectiveness in three typical dynamic OSN applications. To the best of our knowledge, this is the first work on reducing the cumulative errors of the ICP methods in dynamic OSNs.
ACM Reference format:
Jingjing Wang, Wenjun Jiang, Kenli Li, and Keqin Li. 2021. Reducing Cumulative Errors of Incremental CP Decomposition in Dynamic Online Social Networks. ACM Trans. Knowl. Discov. Data 15, 3, Article 42 (April 2021), 33 pages. https://doi.org/10.1145/3441645
1 INTRODUCTION
The CANDECOMP/PARAFAC (CP) decomposition can naturally represent high-dimensional data without loss of information and capture the underline interactions with high interpretability. Therefore, it is widely used in social network analysis [13, 25, 38], such as network reconstruction [38], popularity prediction [13, 19], link prediction [8, 11, 52], and recommendation system [14]. Beyond traditional static setting, large amounts of new data are produced rapidly in real-world applications. For example, Instagram users post 277,777 stories and Twitter users post 511,200 tweets every single minute in 2019.1 So, it is almost impossible to obtain the global data at once. Even if the global data are already available, the computation of the CP decomposition is extremely expensive due to high time and space complexity. Moreover, the changing nature of data evolving over time makes the CP decomposition inefficient [59, 60].
Recently, more and more incremental CP decomposition (ICP) methods have been developed for dynamic data over time, which incrementally maintain the CP decomposition of an evolving tensor, by updating previous CP decomposition results based on newly added data [16, 31, 59, 60]. They are efficient because they reuse the previous results. However, the approximations in incremental updates cause errors. Moreover, with the increase of new data, the errors increase cumulatively, leading to the serious deviation from the optimal CP decomposition. So, their accuracy decreases over time quickly in dynamic online social network (OSN) applications.
We check the performance of an ICP method [60] in three dynamic OSN applications (Figure 1): dynamic network reconstruction, popularity prediction, and link prediction. We first build an initial tensor $\mathcal {X}^{(0)}$ based on the observable data and conduct its CP decomposition as initialization. Then, we conduct the ICP method [60] to incrementally reconstruct the network, predict popularity, and predict links respectively based on new data $\Delta \mathcal {X}^{(t)} \,(t\in [1,T])$. Detailed settings are the same as that in Sections 5–7. We find that the accuracy of the ICP method decreases over time quickly. In addition, it shows non-uniform error accumulation in different time periods.
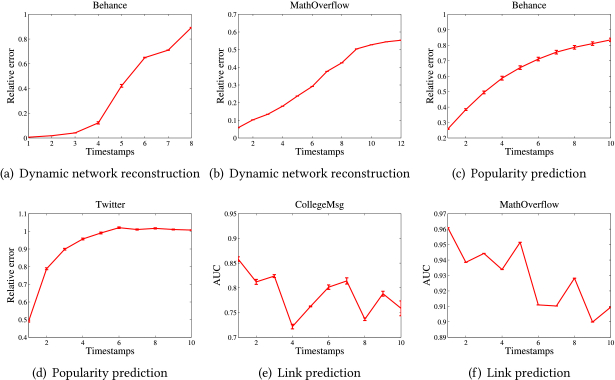
The above experiments validate the existence of cumulative errors of the ICP methods in dynamic OSNs. However, as far as we know, there is no work on reducing the cumulative errors. Thus, there is an urgent need for effective algorithms to improve the accuracy of ICP and promote its applications in OSNs.
In this article, we strive to reduce the cumulative errors of ICP in time while ensuring a high efficiency. Our motivations are threefold: (1) identifying the general types of errors generated by ICP in different applications and studying their fundamental causes. (2) Designing different error reduction strategies according to different types of errors. (3) Checking the effectiveness of different strategies in real OSN applications.
Our basic idea is to restart the CP decomposition, by re-performing full CP decomposition on the tensor combining the new tensor with the old one at certain time points. However, there are two main challenges have to be addressed, as follows:
(1) Challenge of errors. In different applications, what errors will be generated by the ICP methods? What are the fundamental causes of these errors? Which types of errors can be reduced by restarting the CP decomposition?
(2) Challenge of restarting. When to restart the CP decomposition? Restarting time points are critical to the ICP method, because the effectiveness and efficiency of the CP decomposition restarting depend on the time points. If restarting too early, it will result in redundant calculation, and lead to the waste of computation resources. If restarting too late, it will cause serious error accumulation, and lead to low accuracy.
Keeping the efficiency and accuracy in mind, we strive to reduce cumulative errors with less restarting times by addressing the above two challenges. Our main contributions are as follows.
(1) We identify the problem of reducing cumulative error of ICP. As far as we know, it is the first article that identify and study the problem. We believe it will help promote the ICP methods in more OSN applications.
(2) We identify two types of errors, i.e., the reconstruction error and the prediction error in ICP. Then we deeply analyze their causes. Based on this, we set our goals as solving two optimization problems, i.e., minimizing the restarting times while keeping a small cumulative reconstruction error, and minimizing the restarting times while keeping a small prediction error.
(3) We propose several heuristic restarting methods to solve the above two problems, and they are based on the time interval, the reconstruction error, the cumulative reconstruction error, the prediction error, the previous feedback, and the number of changed edges, respectively. We also deeply discuss the relations among these restarting methods, compare their features, highlight their advantages and point out possible extensions.
(4) In order to validate the effectiveness of our methods, we apply them in three typical dynamic OSN applications of network reconstruction, link prediction, and popularity prediction. We conduct extensive experiments on several real-world datasets, and determine the best restarting method for different applications. Moreover, through comparative study with other incremental and non-incremental methods, we provide some guidelines for ICP in future large and incremental data applications.
The remaining of this article is organized as follows. Section 2 reviews the related work. Section 3 defines two optimization problems for cumulative error reduction. Section 4 proposes several restarting methods for addressing the two problems. Sections 5–7 apply our methods in different OSN applications, respectively. Finally, Section 8 concludes the article.
2 RELATED WORK
2.1 Typical Applications in OSNs
Social networks analysis and applications have attracted much attention [20, 22, 49]. We review three typical and important applications in this article, as follows.
Network reconstruction aims to infer the network of interactions from the observed functional behavior [30, 57], which is important for better grasping actual functioning of networks [18, 42]. Network reconstruction has been used widely in social networks [10], web networks [40], news spread networks [36], biochemical reaction networks [57], and biologically inspired networks [9]. In this article, similar to [10, 60], the goal of dynamic network reconstruction is to reconstruct the given network structure information at each time slice.
Link prediction is used to predict future possible links in the network, or predict missing links due to incomplete data [32], which have been proposed in social networks analysis for decades. Many researchers summarize existing work [3, 33, 34, 51], and they usually classify link prediction techniques into several groups, such as similarity-based methods, probabilistic and statistical methods, and factorization-based methods [34].
Among all methods, factorization-based methods have attracted much attention [8, 35], because matrix factorization or tensor factorization models can extract and use latent features from the topological structure to perform prediction. Early works mainly adopt matrix factorization-based techniques to predict link, such as supervised matrix factorization approach [35], singular value decomposition (SVD) [37], non-matrix factorization approach [61], a graph regularized link matrix factorization [12] and so on [26]. Other studies extend matrix factorization-based techniques to coupled analysis of multi-relational data in the form of high-order tensor. Dunlavy et al. [2, 8] use the CP decomposition to address the problem of temporal link prediction, that is, predicting future links based on past data, and illustrate the usefulness of exploiting the natural three-dimensional structure. However, these works above are based on the static graph. Most recently, Zhang et al. [10] propose Theoretically Instructed Maximum-Error-bounded Restart of SVD (TIMERS) based on incremental SVD to predict link, which satisfies the dynamic nature of OSNs.
Popularity prediction aims to predict the popularity of a topic at a reference time $t$, given the diffusion information of this topic before an indicating time $t_0$ $(t_0\lt t)$. Existing works can be generally classified into three categories: (1) classification prediction that predicts whether a topic will be popular or not [54, 55]; (2) ranking prediction that ranks and identifies the most important contents based on their predicted popularity [45, 47]; and (3) precise prediction that predicts how many users will react to a topic [4, 5]. The first two categories obtain higher accuracy to some degree, but they sacrifice the details.
Most works on precise prediction are usually from either the macro or the micro perspective. The former predicts the popularity-level popularity [41, 44], i.e., how many users in total will react a topic. The latter predicts the user-level popularity [21, 28], i.e, estimates the propagation probability that a topic propagates from an individual to another. Most recently, [19] proposes and addresses the problem of group-level popularity prediction, which costs small computation than the user-level prediction, and is more detailed than popularity prediction.
2.2 CP Decomposition and Incremental CP Decomposition
CP decomposition is a low-rank tensor approximation technique, which decomposes a tensor into a sum of component rank-one tensors [15]. Because it can capture the underline structure of high-dimensional data and yield a highly interpretable factorization, it is widely used in OSN applications [2, 8, 16, 19, 25, 38, 38]. However, the CP decomposition is unpractical in real-word OSNs because of two limitations: (1) it is a batch method based on the global data, which is difficult and time consuming for tons of data. (2) It is based on the static networks, which cannot meet the fact that OSNs are dynamic in nature. Nodes and edges may be added or deleted at any time. These dynamic changes make the CP decomposition unpractical.
More and more ICP methods have been developed to track the CP decomposition online of incremental tensor, which mine the feature of newly added data, and update the previous results instead of full re-computation. Gujral et al. [16] propose a Sampling-based Batch Incremental Tensor Decomposition algorithm, SAMBATEN, based on CP decomposition. Zhou et al. [60] propose an efficient incremental CP algorithm (OnlineCP) for online tensors with an arbitrary number of dimensions. They further propose a new OnlineSCP algorithm for tracking the CP decomposition of online sparse tensor [59]. Li et al. [31] propose an Online Robust Low-rank Tensor Modeling method to learn low-rank structures of streaming noisy tensor data robustly.
Existing ICP methods can explore and extract the underlying structure of incremental tensor with high efficiency, and meet the dynamic nature of data evolving over time in OSNs. However, low accuracy is a serious obstacle when it is applied in the social network analysis (see Figure 1). Because all the ICP methods make various approximations in their incremental updating process, error accumulation is inevitable as newly added data keeps coming.
In order to further promote the widespread use of ICP in OSNs, we focus on improving its accuracy while ensuring high efficiency. Our differences from other works are threshold: (1) we try to identify general types of errors, i.e., the reconstruction error and the prediction error in ICP. (2) We strive to design several heuristic restarting strategies to reduce those errors while ensuring a high efficiency. (3) We verify the effectiveness of our restarting methods in three dynamic OSN applications of network reconstruction [10], link prediction [34] and popularity prediction [13, 46].
3 PROBLEM DEFINITION AND SOLUTION OVERVIEW
We identify two types of errors (i.e., the cumulative reconstruction error and the prediction error), and study their fundamental causes. Then, we propose two cumulative error reduction problems based on the two errors. Next, we introduce the overview of our solutions. The notations used in this article are displayed in Table 1.
| Notation | Explanation |
|---|---|
| $\delta$ | the threshold of time interval (or the number of timestamps) for F-time |
| $\theta$ | the threshold of cumulative error for F-Cumerror |
| $\sigma$ | the threshold of reconstruction error for F-Recerror |
| $\xi$ | the threshold of prediction error for F-feedback |
| $\eta$ | the threshold of the number of changed edges for F-changes |
| $\Omega$ | mask tensor to indicate the observable data |
| $J$ | reconstructive error between factor matrices and tensor |
| $\Delta {J}$ | cumulative reconstruction error caused by ICP |
| $\Delta {I}$ | prediction error caused by ICP |
| $t,T$ | the variable of timestamps. $T$ is the maximum dynamic timestamp |
| $x,{\bf x},{\bf X},\mathcal {X}$ | Scalar, vector, matrix, and tensor |
| $\Delta \mathcal {X}$ | a newly added tensor |
| ${\bf A}_1,\ldots , {\bf A}_N$ | factor matrices of an N-order tensor. |
| ${\bf A}\ast {\bf B},\Vert \cdot \Vert$ | element-wise tensor product, Frobenius norm. |
 |
Kronecker product of factor matrices |
3.1 Concepts
Given an $N$-order tensor $\mathcal {X}$ and its factor matrices ${\bf A}_1,\ldots {\bf A}_i,\ldots {\bf A}_N$ obtained by the CP decomposition or the ICP methods, the reconstruction error refers to the loss between the reconstructed tensor by these factor matrices and the original tensor, denoted by $\mathcal {J}$:
In Figures 2
by appending newly added data
at its time mode. Every time a newly added tensor
$\mathcal {X}_{new}$ comes, the CP decomposition must calculate the combined tensor
$\mathcal {X}$ and compute its factor matrices
${\bf A}$, and
${\bf C}$ from scratch (see Figure
2). So, the reconstruction error of the CP decomposition is
Since the CP decomposition is a low-rank tensor approximation technique, its reconstruction error always exists, even for the optimal CP decomposition. In addition, all ICP methods make some approximations in the incremental updating process. The reconstruction error of ICP is constituted by both the intrinsic error in CP decomposition (i.e., the minimum reconstruction error by the optimal CP decomposition) and the cumulative reconstruction error caused by approximations in incremental updates. Details are as follows.
The cumulative reconstruction error of ICP refers to the reconstruction error caused by incremental updates of ICP, excluding the reconstruction loss by the optimal CP decomposition. For the same incremental tensor, suppose its reconstruction errors by the optimal CP decomposition and the ICP decomposition are $\mathcal {J}^{oCP}$ and $\mathcal {J}^{ICP}$, respectively. Then, the cumulative reconstruction error $\Delta \mathcal {J}$ caused by ICP can be calculated as follows:
| Methods | Problems | Worst case | Best case | Mechanism |
|---|---|---|---|---|
| F-time | P1, P2 | $O(NRST^2t_{new})$ | $O(Tf)$ | Time-based, periodical |
| F-Cumerror | P1, P2 | $O(Tf+NRST^2t_{new})$ | $O(Tf+NRST^2t_{new})$ | Cumulative error |
| F-Recerror | P1 | $O(NRST^2t_{new})$ | $O(Tf)$ | Reconstruction error |
| F-feedback | P2 | $O(NRST^2t_{new})$ | $O(Tf)$ | Previous results |
| F-changes | P2 | $ O(NRST^2t_{new})$ | $O(Tf)$ | Changes-based, periodical |
| $^{1}$The time complexity of an ICP method for processing each new data $\Delta \mathcal {X}$ is denoted by $f$. $^{2}$The average complexity of the CP decomposition for $\Delta \mathcal {X}$ is $O(NRSTt_{new})$. |
||||
We also take Figures 2 and 3 as examples. For the same incremental tensor, suppose the CP decomposition in Figure 2 is the optimal CP decomposition with minimum intrinsic error. According to Definition 3.2 and Equations (2) and (3), the cumulative reconstruction error of ICP in Figure 3 can be calculated as follows:
In prediction tasks, the prediction error refers to the error between predicted values by the ICP methods and the true values, denoted by $\Delta \mathcal {I}$. For an incremental tensor $\mathcal {X}$ where some data is missing and needs to be predicted, suppose its ground truth tensor is $\mathcal {X}^{\prime }$, and the reconstructed tensor by ICP is $\widehat{\mathcal {X}}$. Then the prediction error $\Delta \mathcal {I}$ can be calculated as follows.
3.2 Fundamental Causes of Errors
Causes for reconstruction error and cumulative reconstruction error. The reconstruction errors always exist in the CP decomposition and the ICP decomposition, even in the optimal CP decomposition. This is because all of them are low-rank tensor approximation techniques. While the cumulative reconstruction error only exists in ICP for an incremental tensor, and it increases as newly added data keeps coming. This is because that the ICP method makes approximation in its incremental updates for each newly added tensor (see Figure 3). In addition, according to Definition 3.2, the increase of the cumulative reconstruction error results in the increase of the overall reconstruction error of ICP.
As mentioned before, the reconstruction error $\mathcal {J}^{ICP}$ by ICP is constituted by both the intrinsic error $\mathcal {J}^{oCP}$ and the cumulative reconstruction error $\Delta \mathcal {J}$. Because $\mathcal {J}^{oCP}$ is intrinsic in the CP decomposition, it cannot be reduced by restarting the CP decomposition. While, the cumulative reconstruction error $\Delta \mathcal {J}(t)$, i.e., the margin between the reconstruction error of ICP and the minimum error of the CP decomposition, can be reduced by restarting.
Causes for prediction error. In prediction tasks, as new data increases, the prediction error of ICP increases cumulatively. There are two main reasons: (1) as newly added tensor increases, the ICP method needs to continuously update incrementally. Due to the approximations in incremental updates, the cumulative reconstruction error and the reconstruction error of the observable data increase, thus the prediction error of the missing data increases. 2) When a new tensor with some missing values comes, the ICP method updates the previous results to get new ones, and predicts the missing data. Then, the ICP method will reuse these new results to update incrementally for the next new tensor. In this process, the prediction results are taken as the true values for the next prediction, which further expand the prediction error.
Restarting the CP decomposition can reduce the cumulative reconstruction error of the observable data, and it also can use the arrived data for prediction. So, the prediction error can be reduced by restarting.
3.3 Problems Definition
In order to reduce serious error accumulation, the ICP methods need to restart CP decomposition sometimes. That is, at some timestamps, it needs to combine the new data with the current one and conduct the CP decomposition on the combined data. Inevitably, restarting CP decomposition is time-consuming and space-consuming. Therefore, we need to determine the proper time points to restart and reduce the number of restarts, so that the ICP methods with restart strategies reach high accuracy and keep high efficiency. Then, the key challenge occurs: What are the appropriate time points to restart the CP decomposition? That is, when to restart the CP decomposition can reduce the number of restarts and keep a high accuracy? Intuitively, we hope to reduce the number of restarts while keeping a low reconstruction error or prediction error. So, according to the defined two types of errors, we formulate our goals into two constrained optimization problems.
P1: Minimizing the restarting times while keeping a small cumulative reconstruction error. We set a tolerance threshold $\alpha _1$ on the cumulative reconstruction error and then minimize the total number of restarts. Formally, we denote the error evaluation function as $\mathcal {G}(\cdot)$ and whether to restart at timestamp $t$ as $b_t\in \lbrace 0,1\rbrace$ $(t\in [1,T])$. Then, the optimization objective is as follows:
For the function $\mathcal {G}(\cdot)$ in the optimization objective of P1 (see Equation (7)), one approach is to directly use $\mathcal {J}^{ICP}(t)$, the reconstruction error of ICP at timestamp $t$. However, according to the causes analysis (in Section 3.2), we know that the reconstruction error $\mathcal {J}^{ICP}(t)$ of ICP at timestamp $t$ is constituted by both the intrinsic error $\mathcal {J}^{oCP}(t)$ and the cumulative reconstruction error $\Delta \mathcal {J}(t)$. What's more, only the cumulative reconstruction error $\Delta \mathcal {J}(t)$, i.e., the margin between the reconstruction error of ICP and the minimum error of the CP decomposition, can be reduced by restarting the CP decomposition. So, it should be the right measure to guide restart. As most applications are sensitive to the maximum error, we define $\mathcal {G}(\cdot)$ as follows:
Taking Figures 2 and 3 as examples, suppose the CP decomposition in Figure 2 is the optimal CP decomposition with minimum intrinsic error. According to Equations (2), (5), and (8), the error evaluation function $\mathcal {G}(\cdot)$ for tensor $\mathcal {X}$ reconstruction can be calculated as follows.
P2: Minimizing the restarting times while keeping a small prediction error. We set a tolerance threshold $\alpha _2$ on the prediction error and then minimize the total number of restarts. Then the optimization objective for problems P2 is as follows:
In dynamic link prediction, we can use the ICP method to predict links or recover the missing links in dynamic networks. Specifically, we first build a link tensor 
for $n$ users in the observable time period $(0,t_0]$, which has three modes, $n$ users, $n$ users and the observable time period $(0,t_0]$. Its element $\mathcal {X}^{(0)}(i,j,k)$ refers to whether there is a link between users $i$ and $j$ at timestamp $k$. We first conduct the CP decomposition on $\mathcal {X}^{(0)}$ to obtain its factor matrices as initialization. Then, as newly added data 
$(t\in [1,T])$ comes, we use ICP to update previous factor matrices and predict the missing links incrementally.
In this application, the area under curve (AUC) score [35, 48] is used to measure the prediction accuracy. For an incremental link tensor ${\mathcal {X}}^{(t)}$ $(t\in [1,T])$ at timestamp $t$, suppose its mask tensor, ground truth tensor and predictive tensor are $\Omega ^{(t)}$, ${\mathcal {X}}^{^{\prime }(t)}$, and $\widehat{\mathcal {X}}^{(t)}$, respectively. Then, we define the accuracy evaluation function $\mathcal {H}$ as follows:
In dynamic popularity prediction, Wang et al. [50] adopt ICP to predict group-level popularity incrementally. As the illustration in Figure 4, for a target topic $p$, they first build a group-level popularity tensor 
, which has three modes, i.e., $(K+1)$ topics (including $K$ similar historical topics of $p$), $l$ user groups, and the observable time period $[0,t_0]$. Its element $\mathcal {X}^{(0)}(i,j,k)$ refers to the accumulative popularity of topic $i$ in group $j$ until timestamp $k$. Then they conduct the CP decomposition on $\mathcal {X}^{(0)}$ to obtain its factor matrices as initialization. As newly added data 
$(t\in [1,T])$ comes, where $p$’s group-level popularity values need to be predicted (see the white part of new data in Figure 4), they use the ICP method to mine the underlying structure of the current combined tensor $\mathcal {X}^{(t)}$ by appending $\Delta \mathcal {X}^{(t)}$, and predict $p$’s group-level popularity at timestamp $t$.
We use the same framework as [50]. For a topic $p$, suppose its predicted group-level popularity in all groups at timestamp $t$ is $\widehat{\mathcal {X}}_{p,j,t}\,(j=1,\ldots ,l)$, and the ground truth is $\mathcal {X}^{^{\prime }}_{p,j,t}\,(j=1,\ldots , l)$. Then, we define the error evaluation function $\mathcal {H}$ as follows:
3.4 Solution Overview
To address the problems P1 and P2, our basic idea is to propose some restarting strategies to make the error evaluation functions (i.e., $\mathcal {G}(\cdot)$ and $\mathcal {H}(\cdot)$) less than the given thresholds (i.e., $\alpha _1$ and $\alpha _2$), and minimize the number of restarts. Thus, we need to find effective indicators of restarting and set appropriate thresholds for these indicators for restarting the CP decomposition in time. In particular, when we use $\mathcal {G}(\cdot)$ and $\mathcal {H}(\cdot)$ in objective functions as indicators, the thresholds in the restarting strategies are the same as the tolerance thresholds $\alpha _1$ and $\alpha _2$ in Equations (7) and (10).
Our solution overview is shown in Figure 5. In this article, we propose several restarting methods for the both problems based on their characteristics. For P1, we propose three heuristic restarting methods, which are based on the time interval (F-time), the reconstruction error (F-Recerror), and the cumulative reconstruction error (F-Cumerror), respectively. For P2, we propose four heuristic restarting methods, which are based on the time interval (F-time), the cumulative reconstruction error (F-Cumerror), the previous feedback (F-feedback), and the newly changed data (F-changes), respectively.
It is worth noting that F-time and F-Cumerror are not limited to a specific application, and they can be used for the both problems in different applications. F-time is based on the time interval from the initial timestamp, and it restarts the CP decomposition once after a fixed time interval. F-Cumerror is based on the relative cumulative reconstruction error (RCRE), whose calculation is different in the two problems. In particular, we only calculate the cumulative reconstruction error of observable data for the problem P2.
4 RESTARTING STRATEGIES FOR CUMULATIVE ERROR REDUCTION OF ICP
We describe our restarting methods for problems P1 and P2, respectively. Then, we theoretically analyze their time complexities. Finally, we discuss their relations, differentiate their features, and point out possible hybrid approaches.
4.1 Restarting Strategies for the Problem P1
The problem P1 is for the dynamic tensor reconstruction tasks in OSNs, whose primal goal is to reconstruct the given dynamic tensor over time, for example, dynamic network reconstruction. Given a dynamic tensor, which evolves along the time mode, we design three restarting strategies (i.e., F-time, F-Recerror, and F-Cumerror) for the ICP method to reconstruct the incremental tensor efficiently and accurately. The processes are shown in Algorithm 1.
To be specific, given an initial $N$-order tensor 
, where the last mode is the time mode, we first conduct the CP decomposition to obtain its factor matrices as the initialization (Line 1 in Algorithm 1). For each newly added data 
$(t\in [1,T])$, we use these restarting strategies to determine whether to restart the CP decomposition or not. If yes, we calculate the current combined tensor $\mathcal {X}^{(t)}$ by appending $\Delta \mathcal {X}^{(t)}$ to the previous tensor $\mathcal {X}^{(t-1)}$ at its time mode, and recalculate its CP decomposition from scratch. Otherwise, we incrementally update the previous decomposition results only based on $\Delta \mathcal {X}^{(t)}$. Details of all restarting strategies are described below.
4.1.1 F-time: Fixing the Time Interval $\delta$. We periodically restart the CP decomposition after a certain time interval $\delta$. The details of F-time are shown in the Procedure of F-time in Algorithm 1 (Lines 2–11). F-time first initiates a variable $c$ for counting time intervals from the initial time $t_0$ (Line 3). Then, for each newly added data 
($t\in [1,T]$), F-time adds $t_{new}$ to the variable $c$, and determines restarting or not. If $c$ is a multiple of $\delta$, F-time calculates the current tensor $\mathcal {X}^{(t)}$ by appending $\Delta \mathcal {X}^{(t)}$ to the previous tensor $\mathcal {X}^{(t-1)}$ along the time mode, and restarts the CP decomposition on $\mathcal {X}^{(t)}$ to obtain its factor matrices ${\bf A}_1^{(t)}, \dots ,{\bf A}_N^{(t)}$ (Lines 6–8); otherwise, it updates the previous results ${\bf A}_1^{(t-1)},\dots {\bf A}_N^{(t-1)}$ to obtain ${\bf A}_1^{(t)},\dots {\bf A}_N^{(t)}$ based on $\Delta \mathcal {X}^{(t)}$ by the updating method $\mathcal {F}(\cdot)$ of ICP (Lines 9–10). Finally, it returns the Kruskal operator of these factor matrices 
as the reconstruction results at timestamp $t$.
Complexity Analysis. The time complexity of the ICP method for a new data slice depends on a specific incremental updating method, and it is related to the size of newly added data [60]. Given an initial $N$-order 
and a new data slice 
($t\in [1,T]$), we suppose ICP ’s time complexity for processing $\Delta \mathcal {X}^{(t)}$ is a function $O(f(N,R,S,t_{new}))$, where $R$ is the rank of the dynamic tensor, indicating the number of latent factors, $S=\prod _{i=1}^{N-1}r_i$, and $St_{new}$ is the size of $\Delta \mathcal {X}^{(t)}$. The time complexity of the CP decomposition is related to the size of the current combined tensor, and it is $O(NRS(t_{0}+t\cdot t_{new}))$ [60], where $(t_{0}+t\cdot t_{new})$ is the size of the combined tensor on the time mode, and $S(t_{0}+t\cdot t_{new})$ is the size of the whole tensor. Since there are $T$ new data $\Delta \mathcal {X}^{(t)}$, its average time complexity is $O(NRS(t_{0}+(1+T)/2\cdot t_{new}))$; the initial observable time $t_0$ is usually much smaller than other factors, so the average time complexity of the CP decomposition is $O(NRSTt_{new})$.
The time complexity of F-time is based on the threshold $\delta$ of time interval. In the worst case, the threshold $\delta$ is smaller than $t_{new}$, then F-time needs to restart the CP decomposition for each new data $\Delta \mathcal {X}$. There are a total of $T$ new data $\Delta \mathcal {X}$, so the total time complexity is $O(NRST^2t_{new})$. Meanwhile, in the best case, the threshold $\delta$ is larger than $t_{new}$, then F-time only calculates ICP for each new data. The total complexity is $O(Tf(N,R,S,t_{new}))$.
4.1.2 F-Recerror: Fixing the Maximum Relative Reconstruction Error $RRE$ by a Threshold $\sigma$. In F-Recerror, we take the relative reconstruction error ($RRE$) as a measure to guide when to restart the CP decomposition. For an $N$-order dynamic tensor $\mathcal {X}^{(t)}$ at timestamp $t$, its RRE is denoted as $RRE(t)$, which is calculated as follows:
The details of F-Recerror are shown in Procedure of F-Recerror of Algorithm 1 (Lines 12–21). For each new data $\Delta \mathcal {X}^{(t)}$ ($t\in [1,T]$), F-Recerror first updates the previous results ${\bf A}_1^{(t-1)},\dots ,{\bf A}_N^{(t-1)}$ to get ${\bf A}_1^{(t)},\dots ,{\bf A}_N^{(t)}$ by the ICP method $\mathcal {F}(\cdot)$ (Lines 13–14). Then, it calculates the current combined tensor $\mathcal {X}^{(t)}$, and $RRE(t)$ with Equation (13) (Lines 15–16). Next, it compares $RRE(t)$ with the threshold $\sigma$ (Lines 17–21): if $RRE(t)$ is greater than $\sigma$, F-Recerror restarts the CP decomposition on $\mathcal {X}^{(t)}$, and returns the reconstruction results; Otherwise, F-Recerror returns 
by the ICP method.
Complexity Analysis. In the worst case, for each new data $\Delta \mathcal {X}$, its $RRE$ is larger than $\sigma$. Then, F-Recerror needs to calculate the ICP method and restart the CP decomposition every time, taking the time complexity of $O(f(N,R,S,t_{new})+NRSTt_{new})$. There are a total of $T$ new data, so the total time complexity is $O(Tf(N,R,S,t_{new})+NRST^2t_{new})$. Meanwhile, in the best case, $RRE$ is less than $\sigma$ for each new data $\Delta \mathcal {X}$. Then, F-Recerror only calculates ICP, whose time complexity is $O(f(N,R,S,t_{new}))$. There are a total of $T$ new data $\Delta \mathcal {X}$, so the total time complexity is $O(Tf(N,R,S,t_{new}))$.
4.1.3 F-Cumerror: Fixing the Maximum Relative Cumulative Reconstruction Error $RCRE_{P1}$ by $\theta$. In this strategy, we focus on the cause that leads to the increase of the reconstruction error $\mathcal {J}^{ICP}$ of ICP. According to the causes analysis in Section 3.2, we know that only the part of the cumulative reconstruction error $\Delta \mathcal {J}$ in $\mathcal {J}^{ICP}$ can be reset by restarting the CP decomposition, thus it could be the right measure to guide restarting. However, it is difficult to calculate the cumulative reconstruction error $\Delta \mathcal {J}(t)$ by $\mathcal {J}^{ICP}(t)-\mathcal {J}^{oCP}(t)$ directly, because the determination of a CP rank is NP-hard [17] and there is no optimal (i.e., minimum) loss $\mathcal {J}^{oCP}$ proved in theory. Thus, we conduct the CP decomposition on dynamic tensor at each timestamp, which serves as the optimal CP decomposition with the minimum loss in this article. The margin between the reconstruction error of ICP and the minimum loss by the optimal CP decomposition, is the actual cumulative reconstruction error $\Delta \mathcal {J}$ induced by incremental updates. We calculate the relative cumulative reconstruction error $RCRE_{P1}(t)$ at timestamp $t$ as follows:
The details of F-Cumerror are shown in Procedure of F-Cumerror of Algorithm 1 (Lines 22–31). For each new data $\Delta \mathcal {X}^{(t)}$ ($t\in [1,T]$), F-Cumerror first updates the previous results to obtain ${\bf A}_1^{(t)},\,\dots ,\,{\bf A}_N^{(t)}$ by the ICP method $\mathcal {F}(\cdot)$ (Line 24). Next, it calculates the current combined tensor $\mathcal {X}^{(t)}$ and conducts the CP decomposition 
(Lines 25–26). Then, it calculates the relative cumulative reconstruction error $RCRE_{P1}(t)$ with Equation (14) (Line 27). By comparing $RCRE_{P1}(t)$ with the given threshold $\theta$, F-Cumerror determines to return the reconstruction result of ${\bf A}_1^{(t)},\,\dots ,\,{\bf A}_N^{(t)}$ by ICP (when $RCRE_{P1}(t)\le \theta$) or that of ${\bf A^{\prime }}_1^{(t)},\,\dots ,\,{\bf A^{\prime }}_N^{(t)}$ by the CP decomposition (when $RCRE_{P1}(t)\gt \theta$) (Lines 28–31).
Complexity Analysis. In order to calculate $RCRE_{P1}(t)$ ($t\in [1,T]$), F-Cumerror has to calculate ICP and the CP decomposition for each new data, no matter restarting or not. So, the time complexity of F-Cumerror is the same as that of F-Recerror in the worst case, and the total time complexity is $O(Tf(N,R,S,t_{new})+NRST^2t_{new})$.
4.2 Restarting Strategies for Problem P2
The problem P2 is for the dynamic prediction tasks in OSNs, whose primal goal is to predict the missing data of the incremental tensor at each timestamp, such as dynamic link prediction and dynamic popularity prediction [7, 23, 53, 58]. Given a dynamic tensor, where some missing values need to be predicted, we design four restarting strategies (i.e., F-time, F-Cumerror, F-feedback, and F-Changs) to determine the appropriate restarting time points. The ICP method with these restarting strategies can predict the missing data incrementally, efficiently and accurately.
Given an initial $N$-order tensor 
, where the last mode is the time mode, and $t_0$ is the observable time period, we first calculate its CP decomposition as initialization (Line 1 in Algorithm 2). For each new data 
($t\in [1,T]$) with some missing values, we use the restarting strategy to determine whether to restart the CP decomposition or not. If restarting, we calculate the CP decomposition on $\mathcal {X}^{(t)}$, which is obtained by appending $\Delta \mathcal {X}^{(t)}$ to the previous tensor $\mathcal {X}^{(t-1)}$ at the time mode. Otherwise, we incrementally update the previous results based on $\Delta \mathcal {X}^{(t)}$ by ICP. Finally, based on these obtained factor matrices, we reconstruct the tensor and predict the missing data in $\Delta \mathcal {X}^{(t)}$. Details of all restarting strategies are as follows.
4.2.1 F-time: Fixing the Time Interval $\delta$. F-time restarts the CP decomposition periodically after each certain time period $\delta$. Its restarting mechanism is the same as that in Section 4.1.1, so we do not repeat its details here. After obtaining the reconstruction result $\widehat{\mathcal {X}}^{(t)}$ for a dynamic tensor $\mathcal {X}^{(t)}$ at timestamp $t$, F-time calculates $({\bf 1}-\Omega ^{(t)})*\widehat{\mathcal {X}}^{(t)}$ as the predicted values, where $\Omega ^{(t)}$ is a mask tensor of $\mathcal {X}^{(t)}$, indicating the observed entries of $\mathcal {X}^{(t)}$.
Complexity Analysis. According to the complexity analysis for F-time in Section 4.1.1, in the worst case, the total time complexity of F-time for P2 is $O(NRST^2t_{new})$, where $O(NRSTt_{new})$ is the average time complexity of the CP decomposition for each new data, and $T$ is the number of newly added data. Meanwhile, in the best case, the total complexity is $O(Tf(N,R,S,t_{new}))$, where $O(f(N,R,S,t_{new}))$ is the time complexity of ICP for processing a new data slice.
4.2.2 F-Cumerror: Fixing the Maximum Relative Cumulative Reconstruction Error $RCRE_{P2}$ by a Threshold $\theta$. The difference between F-Cumerror here and the previous one for problem P1 in Section 4.1.3 is the calculation of relative cumulative reconstruction error $RCRE_{P2}$. For problem P2, F-Cumerror only calculates $RCRE_{P2}$ of observable data. So, we redefine $RCRE_{P2}(t)$ at timestamp $t$ as follows:
The details of F-Cumerror are shown in Procedure of F-Cumerror of Algorithm 2 (Lines 2–10). For each new tensor $\Delta \mathcal {X}^{(t)}$ ($t\in [1,T]$) with some missing values, F-Cumerror first incrementally updates the previous results to obtain ${\bf A}_1^{(t)},\,\dots ,\,{\bf A}_N^{(t)}$ by the ICP method $\mathcal {F}(\cdot)$ (Line 4). Next, it calculates the CP decomposition on the current combined tensor 
(Line 5). Based on the above results, it calculates $RCRE_{P2}(t)$ with Equation (15) (Line 6). Then, comparing $RCRE_{P2}(t)$ with the given threshold $\theta$, F-Cumerror decides restarting or not (Lines 7–9): if $RCRE_{P2}(t)$ is greater than $\theta$, it calculates the reconstruction tensor 
;
otherwise, 
. Finally, based on $\widehat{\mathcal {X}}^{(t)}$ and the mask tensor $\Omega ^{(t)}$, F-Cumerror returns the predictive values at timestamp $t$ (Line 10).
Complexity Analysis. No matter restarting or not, F-Cumerror has to calculate the CP decomposition and ICP for each new data for calculating $RCRE_{P2}(t)$, whose time complexity is $O(f(N,R,S,t_{new})+NRSTt_{new})$. There are a total of $T$ new data slices, so the total time complexity is $O(Tf(N,R,S,t_{new})+NRST^2t_{new})$.
4.2.3 F-feedback: Fixing the Previous Feedback by a Threshold $\xi$. This strategy is a purpose-driven strategy. For an incremental tensor $\mathcal {X}^{(t)}$ ($t\in [1,T]$), the prediction error $\mathcal {H}(\mathcal {X}^{^{\prime }(t-1)},\widehat{\mathcal {X}}^{(t-1)},\Omega ^{(t-1)})$ (see Equation (10) for the problem P2) at timestamp $t-1$ severs as feedback to guide whether to restart at timestamp $t$. $\mathcal {X}^{^{\prime }(t-1)},\,\widehat{\mathcal {X}}^{(t-1)}$, and $\Omega ^{(t-1)}$ are the ground truth tensor, the predicted tensor, and the mask tensor of $\mathcal {X}^{(t-1)}$, respectively. It is worth noting that the error evaluation function $\mathcal {H}(\cdot)$ has different forms in specific prediction tasks. For example, $\mathcal {H}(\cdot)$ can be expressed as the AUC score in dynamic link prediction (see Equation (11)), and the relative mean error of group-level (REG) in dynamic popularity prediction (see Equation (12)), respectively.
The Procedure of F-feedback in Algorithm 2 (Lines 11–24) shows its details. F-feedback introduces a variable $flag$ to indicate whether to restart or not, which is initialized as 0 (Line 12). For each new data $\Delta \mathcal {X}^{(t)}$ (Lines 13–19): if $flag$ equals 1, F-feedback restarts the CP decomposition on the current tensor $\mathcal {X}^{(t)}$, and obtains factor matrices ${{\bf A}_1^{(t)},\dots ,{\bf A}_N^{(t)}}$; otherwise, it incrementally updates previous results to obtain ${{\bf A}_1^{(t)},\dots ,{\bf A}_N^{(t)}}$ by $\mathcal {F}(\cdot)$; based on the reconstruction tensor of these factor matrices and the mask tensor $\Omega ^{(t)}$, F-feedback obtains predicted values at timestamp $t$. Finally, it calculates $\mathcal {H}(\cdot)$ at timestamp $t$ based on the predicted values and their ground truth, and sets $flag$ by comparing $\mathcal {H}(\cdot)$ and the given threshold $\xi$ (Lines 20–24). Specifically, when $\mathcal {H}(\,\cdot)$ is a measure of prediction error, $flag$ is set as 1 (if $\mathcal {H}(\cdot)$ > $\xi$), or 0 (if $\mathcal {H}(\cdot)\le \xi$); when $\mathcal {H}(\cdot)$ is a measure of accuracy, $flag$ is set as 1 (if $\mathcal {H}(\cdot)\lt \xi$), or 0 (if $\mathcal {H}(\cdot)\ge \xi$).
Complexity Analysis. In the worst case, $flag$ is always 1. Then, F-feedback needs to recalculate the CP decomposition for each new data $\Delta \mathcal {X}^{(t)}$ $t\in [1,T]$, whose time complexity is $O(NRTSt_{new})$. There are a total of $T$ new data slices, so the total time complexity of prediction process is $O(NRT^2St_{new})$. In the best case, $flag$ is always 0. Then, F-feedback only calculates incremental updates for each $\Delta \mathcal {X}$, whose time complexity is $O(f(N,R,S,t_{new}))$. So the total time complexity of prediction process is $O(Tf(N,R,S,t_{new}))$.
4.2.4 F-changes: Fixing the Number of Newly Changed Edges by the Threshold $\eta$. F-changes restarts the CP decomposition after a fixed number of changed edges. The details of F-changes are shown in Procedure of F-changes of Algorithm 2 (Lines 25–36). It first introduces a variable $add\_link$ to count the number of newly added links from the last restarting (Line 26). For each new data $\Delta \mathcal {X}^{(t)}$ ($t\in [1,T]$), it adds the number of links in $\Delta \mathcal {X}$ to $add\_link$ (Line 28), and compares $add\_link$ with the given threshold $\eta$ (Lines 29–34): if $add\_link$ is bigger than $\eta$, F-changes restarts and resets $add\_link$ as 0; otherwise, it uses $\mathcal {F}(\cdot)$ to update the factor matrices. Finally, F-changes reconstructs the predicted tensor $\widehat{\mathcal {X}}_{t}$ based on the factor matrices, and returns the prediction results $({\bf 1}-\Omega ^{(t)})\ast \widehat{\mathcal {X}}^{(t)}$ at timestamp $t$ (Lines 35–36).
Complexity Analysis. In the worst case, $\eta$ is very small, and the number of new added links in $\Delta \mathcal {X}^{(t)}$ $t\in [1,T]$ is larger than $\eta$. F-changes needs to recalculate the CP decomposition for each new data. There are a total of $T$ new data slices, so the total time complexity is $O(NRST^2t_{new})$. In the best case, $\eta$ is very large. Then, F-changes does not restart, and only calculates ICP for each new data. So the total time complexity is $O(Tf(N,R,S,t_{new}))$.
4.3 Discussion
We propose several restarting methods for addressing the two problems P1 and P2. They have no specific requirements on the ICP method or the incremental updating method. Therefore, they are flexible to cooperate with any ICP methods. Now, we compare their main features, and discuss the possible extended restarting methods.
4.3.1 Main Features. We compare all restarting methods on three main features, including the problems they are suitable for, their time complexities, and their restarting mechanisms and threshold setting strategies. The results are shown in Table 2, where $f$ is a function $f(N,R,S,t_{new})$ ($S=\prod _{i=1}^{N-1}r_i$), referring to the time complexity of a specific ICP method for processing each newly added data $\Delta \mathcal {X}$.
Problems. Among all the five restarting methods, F-Recerror is suitable for P1 only. F-feedback and F-changes are suitable for P2. Meanwhile, F-time and F-Cumerror are not limited to specific problems or applications. They can be used for both problems P1 and P2. F-time restarts the CP decomposition once after a fixed time interval. F-Cumerror is based on the RCRE. Note that, F-Cumerror for P2 only calculates the RCRE of observable data, while it is all data for P1.
Time complexity. Among all the five methods, four heuristic restarting methods (i.e., F-time, F-Recerror, F-feedback, and F-changes) have the same time complexity both in the worst case and the best case. This is because they only calculate either incremental updates of ICP (in the best case) or the CP decomposition (in the worst case) for each new data. As for F-Cumerror, it has to calculate incremental updates of ICP and the CP decomposition for each new data, no matter restarts or not. So, F-Cumerror costs more time than other methods.
Restarting mechanism and threshold setting. The proposed five restarting methods have different restarting mechanisms and threshold settings. We classify them into three types: periodic restarting, error-based restarting, and feedback-based restarting. Details are as follows.
(1) Periodic restarting. F-time and F-changes periodically restart after a certain time interval and a certain number of changes, respectively. They only need counters to count time interval or the number of changed edges, and then determine whether to restart based on the counters and the given thresholds. So, both of them are efficient and easy to implement.
The thresholds for periodic restarting methods, i.e., time interval $\delta$ for F-time and the number $\eta$ of changed edges for F-changes, depend on the speed of increasing data and the amount of each new data slice, respectively. In order to reduce the number of restarts while keeping a high accuracy, when data increase rapidly and the amount of new data is large, small thresholds are required; when data increase slowly and the amount of new data is small, large thresholds are suitable.
(2) Error-based restarting. F-Cumerror and F-Recerror are based on RCRE and RRE, respectively. According to the cause analysis for errors in Section 3.3, RCRE induced by incremental updates of ICP can be reset by restarting the CP decomposition; while RRE includes the intrinsic loss in the CP decomposition, which still exists even after restarting. So, RCRE is more suitable to guide restarting than RRE.
Thresholds for error-based restarting methods mainly depend on user's tolerance to error. For F-Recerror, its threshold depends on the user's requirements for reconstruction accuracy. The smaller the threshold is, the more restarts it requires, and the closer the obtained result is to the original tensor. Meanwhile, the threshold of F-Cumerror depends on user's tolerance to cumulative error. The smaller the threshold is, the closer the obtained result is to the optimal CP decomposition.
(3) Feedback-based restarting. F-feedback is a purpose-driven method, which determines adaptively restarting or not by monitoring the previous prediction results. For example, when we set the threshold of relative prediction error is $5\%$, it will restart the CP decomposition when the last relative prediction error is bigger than $5\%$. So, F-feedback can restart in time and flexibly, and achieve a stable performance.
The threshold for feedback-based restarting method depends on user's tolerance to prediction error. The smaller the threshold is, the more restarts it needs, and the smaller its prediction error is.
4.3.2 Possible Extensions. We can combine two or more restarting strategies for a hybrid restarting framework. Here, we take the hybrid method $H1(\delta , \theta)$ by combining F-time with the threshold $\delta$ of time interval and F-Cumerror with $\theta$ as an example. When the time interval of new data slices is a multiple of the given threshold $\delta$, $H1$ calculates the $RCRE$; if $RCRE$ is larger than the given threshold $\theta$, it restarts the CP decomposition; otherwise, it updates the previous results incrementally by ICP. Compared with F-time, it does not need to restart the CP decomposition in every $\delta$ time interval. Compared with F-Cumerror, it only calculates $RCRE$ once for $\delta$ time interval. Therefore, the hybrid restarting method would be more flexible and efficient.
In this article, we strive to explore good indicators to guide restarting. Therefore, we mainly study single indicators and check their effects. We will study more hybrid approaches in future work.
5 APPLICATION OF PROBLEM P1: DYNAMIC NETWORK RECONSTRUCTION
In this section, we evaluate the empirical performance of our restarting strategies for problem P1 in dynamic network reconstruction, which aims to reconstruct the given dynamic network tensor.
5.1 Experimental Setup
Datasets. We use two real dynamic social networks with different applications for our experiments, Behance [19] and MathOverflow [39]. The statistics are summarized in Table 3.
| $\#$Timestamps | Timestamp size | Total size | Initial size | Type | |
|---|---|---|---|---|---|
| Behance | 60 | 4 hours | 1,326$\times 12\times$60 | 1,326$\times 12\times$12 | Directed weighted |
| MathOverflow | 50 | 1 week | 1,000$\times$1,000$\times$50 | 1,000$\times$1,000$\times$10 | Undirected unweighted |
Behance 2 (for information diffusion): A dynamic tensor can be established based on the propagation of multiple topics (i.e., projects) on all user groups over time. It is a third-order tensor of size $1,326\, (topics)\times 12\,(user\, groups)\times 60 \,(timestamps)$, whose element refers to the cumulative appreciating number of a project in an user group until a certain time. The size of the initial tensor is $1,326\times 12\times 12$.
MathOverflow 3 (for link prediction): It is a dynamic network of interactions, which are represented as undirected links between user nodes with timestamps. After filtering and removing inactive users, the dataset can build a dynamic tensor with binary entries of size 1,000 $(users)\,\times\,$ 1,000 $(users)\times 50\,(timestamps)$, whose element refers to whether there is an interaction between two users at a certain time. The size of the initial tensor is 1,000 $\times$ 1,000 $ \times\, 10$.
Experimental Settings. Given an initial dynamic network tensor 
, first, all methods calculate the CP decomposition on $\mathcal {X}^{(0)}$ to obtain factor matrices as initialization. Then, for each newly added network tensor 
, different restarting methods are exploited to decide whether to restart the CP decomposition individually. If a method decides not to restart, we use the ICP method [60] to incrementally update the previous results. Otherwise, we use the batch hot of CP decomposition [60], which uses the CP decomposition of the last timestamp as the initialization for decomposing the current tensor. Finally, we obtain the reconstruction tensor based on these decomposition results. We run each method with a certain parameter 10 times, and report the average results and their deviations.
Parameter Settings. Tensor decomposition can preserve most significant information when rank $R$ is small (i.e., low-rank decomposition) while saving space [25]. So, we use low-rank $R=2$ across all experiments unless specified. In addition, the threshold $\delta$ of time interval for F-time can be simplified to represent the number of timestamps, because the datasets have been partitioned into equal-time intervals. For example, when $\delta =2$ on Mathoverflow, F-time periodically restarts the CP decomposition after 2 timestamps (i.e., 2 weeks).
Baselines. We implement ICP with different restarting strategies, and compare them with the ICP method itself [60] to check the effects of the different restarting methods on ICP in dynamic network reconstructions.
Metrics. To evaluate the effectiveness of restarting, we use relative error as follows to evaluate how well different methods can approximate the performance of the optimal CP decomposition.
5.2 Experimental Results
5.2.1 Performance and Parametric Sensitivity. We analyze the threshold sensitivity of different restart methods. For F-time, we vary $\delta$ from 1 to 5, then it restarts $48,\, 24,\, 16,\,12, and \,9$ times successively on Behance, and $40,\, 20,\, 13,\,10, and \,8$ times on Mathoverflow. For F-Recerror and F-Cumerror, we adjust their thresholds to make them have the average number of restarts from 9 to 48 on Behance, and from 8 to 40 on Mathoverflow. We compare their relative error and average running time as in Figures 6 and 7, respectively.
The effect of thresholds on relative error. For F-time (Figures 6(a) and (d)), its $RE(t)$ curves fluctuate regularly over time, and have multiple peaks and valleys. Moreover, with the increase of $\delta$, the time interval between valleys increases, and the value of $RE(t)$ increases at the same timestamp. This is because with the increase of $\delta$, its restarting times decrease.
For F-Recerror (Figures 6(b) and (e)), the $RE(t)$ curves have a period of stability, when the results are very close to that of the optimal CP decomposition (i.e., $RE(t)$ is almost equal to 0 in the beginning on Behance or in the end on MathOverflow). The smaller the threshold $\sigma$ is, the larger the number of restarting is, the smaller $RE(t)$ is, and the longer the stationary period is.
For F-Cumerror (Figures 6(c) and (f)), its $RE(t)$ curves have many peaks and valleys. Unlike F-time, its time interval between peak or valleys is not fixed, and has no apparent pattern. In addition, at the same timestamp, the bigger $\theta$ is, the bigger $RE(t)$ is.
The effect of thresholds on running time. Figure 7 shows that the running time curves of F-time, F-Cumerror, and F-Recerror increase over timestamps. This indicates that with the increase of newly added data, their running time increases. For F-time (Figures 7(a) and (d)) and F-Recerror (Figures 7(b) and (e)), at the same timestamps, with the increase of their thresholds, their running time decreases. Meanwhile, the changes of thresholds $\theta$ for F-Cumerror have little effects on the running time. That is, at the same timestamp, the running time remains constant for different thresholds. This is because that for each new data, F-Cumerror has to calculate the CP decomposition, ICP, and the cumulative reconstruction error, no matter restarting or not.
The effect of tensor density. We test the effect of tensor density on the running time by F-time with $\delta = 1$ as shown in Figure 8. We randomly hide $10\%$, $20\%$, $30\%$, $40\%$, and $50\%$ links of Mathoverflow, respectively, and we denote the rest network datasets as $M1$, $M2$, $M3$, $M4$, and $M5$, respectively. We calculate their densities as shown in Table 4. We run 10 rounds on each dynamic network and report the average results. Figure 8 shows that the average running time of F-time grows near-linearly with density, and a larger density leads to a longer running time.
| Datasets | M1 | M2 | M3 | M4 | M5 |
|---|---|---|---|---|---|
| Density | 1.5‰ | 1.3‰ | 1.1‰ | 1‰ | 0.8‰ |
The effect of rank $R$. We study the effect of different ranks by comparing all algorithms with varying $R$ from 1 to $t_0$ (i.e., $R$ from 1 to 12 on Behance, and from 1 to 10 on MathOverflow). The results are shown in Figure 9.
In general, the increase of rank $R$ do affect the relative error, the average running time and the number of restarts. With different ranks $R$, ICP with restarting methods have much lower relative errors than ICP itself, while their running time is a bit longer. For instance, compared with ICP itself on MathOverflow (Figures 9(d) and (e)), when $R=1$, ICP with F-time restarting method reduces the relative error by $95.6\%$ with the cost of 10.5x running time; When $R=10$, it reduces the relative error by $87.1\%$, with the cost of 14.2x running time. Details are as follows.
(1) Accuracy (Figures 9(a) and (d)). With the increase of $R$, the relative error of ICP decreases, and that of ICP with restarting methods has slight changes. What's more, ICP with our restarting methods has much lower relative error than ICP itself. So, ICP with our restarting methods provide more stable and higher accuracy results than ICP itself. (2) Efficiency (Figures 9(b) and (e)). As $R$ increases, the running time of all methods increases, because their time complexities are linearly related to $R$. (3) Number of restarts (Figures 9(c) and (f)). With the increase of $R$, the number of restarts of F-time remains constant; that of F-Recerror decreases due to the decrease of reconstruction error; and that of F-Cumerror increases due to the increases of the RCRE (see Section 4.1.3). Meanwhile, the number of restarts of ICP is 0, i.e., it only conducts the incremental updates on new data.
Taking all together, for different $R$, ICP with our restarting methods has smaller relative error at the expense of a little time, and they provide more stable results than ICP itself. Furthermore, we find that ICP with restarting methods or itself can preserve most significant information when R is small (i.e., low-rank decomposition), while saving space and running time. Hence, in the following experiments, we set a low rank $R=2$ in all three OSN applications.
5.2.2 Comparative Study. We first compare the proposed different restarting methods in details. Then, our methods are compared with the baseline in terms of accuracy and efficiency.
Number of restarts. We compare the number of restarts of our methods when fixing their relative error. We adjust the thresholds of F-time, F-Recerror, and F-Cumerror, so that all methods achieve the same maximum error. The results are displayed in Figure 10. It shows that F-Cumerror outperforms other two methods, i.e., it significantly reduces the number of restarts while maintains the same maximum error. Compared with F-Recerror, F-Cumerror reduces the number of restarts by $50.5\%$ on Behance, and by $78.7\%$ on MathOverflow.
Relative error. We compare the relative error of our methods when fixing their number of restarts by adjusting their thresholds. The results are shown in Table 5. We observe that the F-Cumerror achieves the smallest relative errors (i.e., $ave(RE)$ and $max(RE)$), followed by F-time. While F-Recerror has the largest relative errors on the two datasets. These results demonstrate that the timestamps of restarting are indeed crucial for the ICP method, and the cumulative error is a good measure to guide when to restart.
| Datasets | Methods | Ave (RE) | Standard deviation | Max (RE) | Running time | |
|---|---|---|---|---|---|---|
| Behance | ICP with restarting | F-time | 0.0611 | 0.0001 | 0.7026 | 0.0034 |
| F-Recerror | 0.1186 | 2.0E-07 | 0.1372 | 0.3265 | ||
| F-Cumerror | 0.0198 | 1.3E-05 | 0.0619 | 0.3297 | ||
| Baseline | ICP | 0.8092 | 0.0138 | 0.9346 | 0.0007 | |
| MathOverflow | ICP with restarting | F-time | 0.0308 | 3.4E-06 | 0.1762 | 0.0788 |
| F-Recerror | 0.2684 | 7.9E-05 | 0.5653 | 0.2983 | ||
| F-Cumerror | 0.0288 | 6.4E-07 | 0.0987 | 0.4831 | ||
| Baseline | ICP | 0.4945 | 0.0001 | 0.5807 | 0.0075 | |
Comparison with baseline. We compare our methods with the baseline in terms of accuracy and efficiency as shown in Table 5. Compared with ICP itself, ICP with restarting methods achieves smaller relative errors and standard deviations at the expense of longer running time.
Accuracy. ICP with our methods have lower relative errors and smaller standard deviations than the baseline of ICP. In particular, ICP with F-Cumerror has the smallest relative error. This indicates that ICP with restarting methods can stably achieve higher accuracy than ICP itself, and the RCRE in F-Cumerror is the good measure to guide when to restart.
Efficiency. ICP costs the least time among all methods, followed by F-time. The restarting mechanism of F-time is simple, it only counts the time intervals for determining whether to restart. Meanwhile, F-Cumerror costs the longest time, because it needs to calculate ICP and the CP decomposition for each new data.
5.3 Brief Summary
In this section, we apply the ICP method with our restarting strategies in dynamic network reconstruction. Based on extensive experiments, two main findings are summarized as follows.
(1) Among three restarting methods for problem P1, F-Cumerror outperforms other two methods: when fixing the number of restarts, F-Cumerror has the minimum error; when fixing the maximum relative error, F-Cumerror requires the minimum number of restarts. These results demonstrate that the time points of restarting CP decomposition are indeed crucial for ICP, and F-Cumerror has better performance in determining the appropriate restarting time.
(2) Taking the accuracy and the efficiency into consideration, we compare our methods with baseline. The results show that ICP with restarting methods costs a little more running time, but it provides more stable and higher accuracy results than ICP itself.
6 APPLICATION OF PROBLEM P2: DYNAMIC LINK PREDICTION
In this section, we evaluate the empirical performance of our restarting strategies for problem P2 in dynamic link prediction, which aims to predict the missing links at each timestamp.
6.1 Experimental Setup
Datasets. We use two real-world datasets of CollegeMsg [43] and MathOverflow [39] for evaluation. Their statistics are summarized in Table 6.
| Time | $\#$Temporal | $\#$Total | $\#$Initial | Timestamp | ||
|---|---|---|---|---|---|---|
| span | $\#$Users | edges | timestamps | timestamps | size | |
| CollegeMsg | 193 days | 1,899 | 59,835 | 28 | 6 | 1 week |
| MathOverflow | 350 days | 1,000 | 506,550 | 50 | 10 | 1 week |
CollegeMsg 4: It is comprised of private messages sent on an OSN at the University of California, Irvine. The link $(u,v,k)$ means that user $u$ sent a private message to user $v$ at time $k$. We filter and remove inactive users who have less interaction with others.
MathOverflow 5: It is the same as the MathOverflow in Section 5.
Evaluation Methods. We randomly hide $10\%$ of the network, and different methods are conducted on the rest of the network to recover the missing data. We run each method with a certain parameter 10 times, and report the average results and their deviations.
Baselines. We compare the ICP method with our restarting strategies, with the ICP method itself [60] and TIMERS [10]. TIMERS is a restarting method based on incremental SVD [6], and is applied to dynamic link prediction. Instead of predicting concrete number of links, TIMERS is to predict the probability of edges between nodes in this article. Its prediction result at timestamp $t$ minus the previous one at timestamp $t-1$ is taken as the prediction result of newly added data.
Metrics. We adopt a standard metric, AUC score [35, 48], in our experiments. We calculate the $AUC$ at each timestamp based on prediction results, denoted as $AUC_t$. The average AUC score is defined as: $avg(AUC)=\frac{1}{T}\sum _{t=1}^{T}AUC_{t}$ for the final accuracy. In addition, we use the average running time for processing one data slice to validate the efficiency of a method.
6.2 Experimental Results
6.2.1 Performance and Parametric Sensitivity. We compare the performance of different restarting methods with different thresholds. For F-time, we vary $\delta$ from 1 to 5, then it restarts $22,\, 11,\, 7,\,5, and\,4$ times successively on College Msg, and restarts $40,\, 20,\, 13,\,10,and \,8$ times successively on Mathoverflow. For the other methods, we adjust their thresholds to make them have the average number of restarts from 4 to 22 on College Msg, and from 8 to 40 on Mathoverflow. The results are shown in Figures 11 and 12, respectively.
The effect of thresholds on AUC. From Figure 11, we find that the AUC curves of different restart strategies fluctuate over time and show a downward trend as a whole. The farther the future is, the harder it is to predict, leading to the decrease of accuracy. At the same timestamp, the AUC scores of F-time, F-Cumerror, and F-changes decline slightly as their thresholds increase. While for F-feedback, the bigger its threshold $\xi$ is, the bigger AUC is.
The effect of thresholds on running time. From Figure 12, we find that for F-time and F-changes, with the increase of thresholds, their average running time decrease, and their curves fluctuate under the curves with smallest thresholds (i.e., F-time with $\delta =1$, F-changes with $\eta =1000$). The difference is that the time intervals between the peaks of F-time are the same, but that of F-changes are different. Meanwhile, for F-Cumerror, it takes almost the same time for different thresholds $\theta$. In addition, for F-feedback, at the same timestamp, the bigger the threshold $\xi$ is, the bigger the average running time is. This is because that with the increase of $\xi$, its tolerance to error decreases, and it needs to restart more times, leading to the increase of the average running time.
6.2.2 Comparative Study. We compare our methods with the baselines, which are also incremental methods. We keep all methods except ICP itself having the same number of restarts by adjusting the thresholds. The results are shown in Table 7.
| Datasets | Methods | AUC | Standard deviation | Running time | |
|---|---|---|---|---|---|
| College Msg | ICP with restarting | F-time | 0.7392 | 0.0039 | 0.1785 |
| F-Cumerror | 0.7369 | 0.0069 | 1.2892 | ||
| F-feedback | 0.7379 | 0.0041 | 0.2241 | ||
| F-changes | 0.741 | 0.0001 | 0.1456 | ||
| Baselines | ICP | 0.7333 | 0.0043 | 0.0253 | |
| TIMERS | 0.5598 | 0.0102 | 3.2758 | ||
| MathOverflow | ICP with restarting | F-time | 0.842 | 6.7E-07 | 0.0789 |
| F-Cumerror | 0.8393 | 3.7E-07 | 0.6121 | ||
| F-feedback | 0.837 | 8.5E-06 | 0.1089 | ||
| F-changes | 0.8426 | 6.9E-07 | 0.0802 | ||
| Baselines | ICP | 0.8178 | 3.2E-05 | 0.0073 | |
| TIMERS | 0.5526 | 0.0058 | 1.4209 | ||
Accuracy. The methods based on the ICP method (i.e., ICP with or without restarting) have higher accuracy and smaller standard deviations than TIMERS. For example, compared with TIMERS, ICP with F-time increases AUC by $32.0\%$ on CollegeMsg, and $52.4\%$ on MathOverflow. This is because as compared with the matrix analysis method (i.e., incremental SVD), the tensor analysis method (i.e., ICP) can capture the underline structure of high-dimensional data. Moreover, ICP with our restarting strategies has higher accuracy than ICP itself, especially for that with F-changes. So F-changes, which restarts based on the amount of newly added links, is a good measure to guide when to restart in links prediction.
In addition, ICP with F-cumerror has higher accuracy but larger standard deviation than ICP itself on CollegeMsg, which means its performance is volatile. It is worth noting that the performance of F-Cumerror here is quite different from that in dynamic networks reconstruction (Section 5), where F-Cumerror has the highest accuracy. These results demonstrate that different restarting methods may be suitable for different applications, and the RCRE may not be a good indicator of restarting for link prediction.
Efficiency. TIMERS costs much longer time than others. The reasons are that for each new data, it needs to calculate the loss bound of incremental SVD, and conduct additional operation to obtain the prediction results due to the limit of matrix. The ICP method with our restarting strategies costs longer time than the original ICP method because of restarting the CP decomposition. It again indicates the importance of minimizing restarting times while keeping higher accuracy.
6.3 Brief Summary
In this section, we apply the ICP method with our restarting strategies in dynamic link prediction. Based on extensive experiments, two main findings are summarized as follows.
(1) When fixing the restarting times, our methods have better performance than the baseline in terms of accuracy and efficiency, especially F-changes.
(2) The type of application has a great impact on the performance of restarting methods. To be specific, F-Cumerror is a good indicator of when to restart for problem P1 in dynamic network reconstruction. While, compared with other restarting methods, it has lower accuracy and longer running time in link prediction.
7 APPLICATION OF PROBLEM P2: DYNAMIC POPULARITY PREDICTION
Now, we evaluate the performance of our methods for problem P2 in dynamic popularity prediction. The primal goal of popularity prediction is to predict the group-level popularity of the target topic incrementally in the future $T$ timestamps, given diffusion information of its historical topics during $T$ timestamps, and its diffusion information during the observable time period $[0,t_0]$ ($t_0\lt T$) [50].
7.1 Experimental Setup
Datasets. We use two real-world datasets of Behance and Twitter in Table 8 for experiments.
| Time span | $\#$Edges | $\#$Topics | Timestamp size | $T$ | $t_0$ | $T-t_0$ | |
|---|---|---|---|---|---|---|---|
| 22,255 | 575,819 | 1,015 | 4 hours | 24 | 5 | 19 | |
| Behance | 85,092 | 13,428,364 | 1,326 | 4 hours | 60 | 12 | 48 |
Behance6 [1]: It is the same as the dataset of Behance in Section 4.
Twitter7 [27, 56]: It is an OSN on which users post and interact with tweets. A topic is a hashtag, whose popularity is the number of times it has been tweeted by users.
Without loss of generality, we convert users networks into undirected networks for simplicity.
Evaluation Methods. Given a target topic $p$, we first adopt the same preprocess as in [19, 50]: using multilevel k-way partitioning algorithm [24] to cluster user into $l$ groups according to users’ activities and the network structure, and selecting top-K similar topics for $p$. Then, we build its initial group-level popularity tensor 
with three modes (i.e., topic mode, user group mode and time mode), whose element $\mathcal {X}^{(0)}_{i,j,k}\,(i\in [1,K+1],j\in [1,l], k\in [1,t_0])$ represents the cumulative popularity of the topic $i$ in group $j$ until the timestamp $k$. As time goes on, new data slices keep coming, where $p$’s group-level popularity is to be predicted. We use ICP with restarting methods to explore the underlying structure incrementally, so as to predict $p$’s group-level popularity at new timestamps incrementally. We run each method with a certain parameter 10 times on all topics, and report their average results.
Complexity Analysis. In order to build a group-level popularity tensor for a topic $p$, we have to cluster users into $l$ groups, and we calculate the Euclidean distance between topics according to their popularity in observable period $(0,t_0]$, so as to select the top-K similar topics. The time complexity of preprocessing is $O(m^2Tl+|E|)$ [50], where $m$ is the total number of candidate similar topics, $l$ is the number of user groups and $|E|$ is the number of edges in the network structure. Combining the time complexity of prediction process in Section 4.2, we can obtain the total time complexity. Taking F-feedback in Section 4.2.3 as an example, its time complexity for popularity prediction in the worst case is $O(NRT^2St_{new})$, where $N=3$ and $S=(K+1)l$. So, in the worst case, the total time complexity of F-feedback for dynamic popularity prediction is $O(m^2Tl+|E|+RT^2Klt_{new})$.
Baselines. We compare the ICP method with our restarting strategies with the classical CP decomposition, the ICP method itself [60] and the most recent group-level prediction method, GPOP [19]. GPOP predicts group-level popularity using the CP decomposition with hierarchical constraints. However, the GPOP model is completed in a single round, thus it cannot update the model and the results incrementally over time.
For fair comparison, we use the same datasets (i.e., Behance and Twitter) and the same settings as in [19, 50], that the number of groups is 12 for Behance, and 11 for Twitter [19], and the number of similar topics is 60 for Behance, and 80 for Twitter [50].
Metrics. We use the standard metric of Root Mean Square Error (RMSE) [29] as the evaluation metric. Moreover, we use the REG specifically defined for group-level popularity prediction in [19], as follows:
7.2 Experimental Results
7.2.1 Performance and Parametric Sensitivity. We compare the performance of different restarting methods with different thresholds. For F-time, we vary $\delta$ from 1 to 5, then it restarts $48,\, 24,\, 16,\,12, and \,9$ times successively on Behance, and $19,\, 9,\, 6,\,4, and\,3$ times successively on Twitter. For other methods, we adjust their thresholds to make them have the average number of restarts from 9 to 48 on Behance and from 3 to 19 on Twitter. The results are shown in Figures 13 and 14, respectively.
The effect of thresholds on RMSE. For F-time (Figure 13(a) and (d)), apart from $\delta =1$, its $RMSE$ curves of F-time fluctuate regularly over time, and have multiple peaks and valleys. These valleys are always on the $RMSE$ curve of F-time with $\delta =1$. In addition, with the increase of $\delta$, the time interval between valleys increases, and the value of $RMSE$ increases at the same timestamp.
For F-Cumerror (Figure 13(b) and (e)) and F-feedback (Figure 13(c) and (f)), their $RMSE$ curves increase linearly over time; meanwhile, at the same timestamp, the bigger their thresholds ($\theta$ for F-Cumerror or $\xi$ for F-feedback) are, the bigger their $RMSE$ values are.
The effect of thresholds on running time. From Figure 14, we find that the running time curves of F-time with $\delta =1$, F-Culerror, F-Recerror, and F-feedback have the same variance tendency. The possible reasons include the amount of new data, the density of tensor, and the training time in the CP decomposition. For F-time (Figure 14(a) and (d)), with the increase of $\delta$, the number of restarts decreases, and the number of peaks decreases. The running time curves of F-time with $\delta =2\sim 5$ fluctuate below that with $\delta =1$. For F-Cumerror (Figures 14(b) and (e)), the change of $\theta$ has little effects on the running time again. For F-feedback (Figures 14(c) and (f)), the bigger its threshold $\xi$ is, the shorter the running time is.
7.2.2 Comparison Study. We first compare our restarting methods in details. Then, ICP with different restarting methods are compared with the baselines in terms of accuracy and efficiency.
Comparison of different restarting methods. The ICP with restarting parts in Table 9 show the results of ICP with our restarting methods when fixing the number of restarts (24 times on Behance and 9 times on Twitter).
| Datasets | Methods | REG | Standard deviation | Running time | |
|---|---|---|---|---|---|
| Behance | ICP with restarting | F-time | 0.2447 | 0.0024 | 0.1624 |
| F-Cumerror | 0.2448 | 0.0037 | 0.3590 | ||
| F-feedback | 0.2488 | 0.0023 | 0.1711 | ||
| Baselines | ICP | 0.9445 | 0.0074 | 0.0227 | |
| GPOP | 0.3174 | 0.0085 | 2.7382 | ||
| CP | 0.9604 | 0.0001 | 0.2033 | ||
| ICP with restarting | F-time | 0.4018 | 0.0033 | 0.0736 | |
| F-Cumerror | 0.5912 | 0.0120 | 0.5912 | ||
| F-feedback | 0.4355 | 0.0033 | 0.0890 | ||
| Baselines | ICP | 0.9961 | 0.0009 | 0.009 | |
| GPOP | 0.7179 | 0.0253 | 6.0791 | ||
| CP | 0.9969 | 0.0001 | 0.1405 | ||
Among all methods, F-time has the smallest relative errors (i.e., REG) and it costs the least running time, followed by F-feedback. It indicates that F-time and F-feedback are more suitable for dynamic popularity prediction. In particular, for determining whether to restart, F-time only counts the time interval instead of calculating errors, which makes it cost less running time. In addition, F-feedback has the minimum standard deviation. This indicates that F-feedback has more stable performance, because of its flexible and adaptive restarting mechanism based on the previous prediction error. While, F-Cumerror here has the maximum REG. This indicates that different restarting methods may be suitable for different applications again, and RCRE is not a good indicator of restarting for popularity prediction.
Comparison with Baselines. We compare our methods with baselines in terms of accuracy and efficiency as shown in Table 9.
Accuracy. ICP with our restarting methods have lower relative errors than all baselines on the two datasets. In particular, ICP with F-time has the lowest REG. Compared with GPOP, ICP with F-time reduces REG by $22.9\%$ on Behance, and $44.0\%$ on Twitter. Meanwhile, it has smaller standard deviation. Among baselines, GPOP has better performance than the other two methods. The CP decomposition and ICP itself have the minimum standard deviation. But, they have much higher prediction error, and cannot be used to predict popularity directly.
Efficiency. ICP with our restarting methods except F-Cumerror achieve higher efficiency than other non-incremental methods (i.e., GPOP and the CP decomposition). The ICP method itself costs the least time, but its prediction accuracy is too low to be applied directly. F-Cumerror needs much time for determining whether to restart, but it still has much higher efficiency than GPOP.
7.3 Brief Summary
In this section, we apply the ICP method with our restarting strategies in dynamic popularity prediction. Based on extensive experiments, three main findings are summarized as follows.
(1) Compared with other restarting methods, F-time has the higher accuracy and efficiency, followed by F-feedback. While, F-Cumerror has the maximum error, which is different from its performance in dynamic networks reconstruction. It indicates that specific restarting methods are required in different applications, and the RCRE is not a good measure to guide restarting in popularity prediction.
(2) Compared with baselines of non-incremental methods, our methods have lower relative error (REG) and higher efficiency, especially F-time. In addition, the ICP method itself costs the lest running time, but its accuracy is too low to be applied to popularity prediction directly.
8 CONCLUSION
8.1 Discussion
In Section 4.3.1, we analyze the main features of different restarting strategies. We classify the proposed strategies into three types: periodic restarting, error-based restarting, and feedback-based restarting, and we provide the general rules of threshold setting. Based on the experiments in three typical applications, here we discuss the threshold setting again.
For F-time, its threshold (i.e., time interval $\delta$) can be set according to the speed of newly added data. When the new data increases fast, we can set $\delta$ to be shorter (e.g., a few hours); when the new data increases slowly, we can set $\delta$ to be longer (e.g., a few weeks). For example, topics usually diffuse fast in OSNs, so, in popularity prediction, we set $\delta$ as 4, 8, or 12 hours. Meanwhile, the links between users usually increase slowly in OSNs, so, in link prediction, we set $\delta$ as 1, $2,$ or 3 weeks.
For F-Recerror and F-Cumerror, their indicators are RRE and RCRE, respectively. So, the range of their thresholds is $[0,1]$. Moreover, according to the analysis in Section 3.2, the reconstruction error includes cumulative reconstruction error, so the threshold of F-Recerror is much larger than that of F-Cumerror in OSN applications.
For F-feedback which adaptively determines restarting by monitoring the previous prediction results, its threshold can be set according to the measure for accuracy. In popularity prediction, we use relative error as the measure, so the threshold can be set as the maximum acceptable error. In link prediction, we use the AUC score as the measure, so the threshold can be set as the minimum expected AUC score.
For F-changes, its threshold can be set according to the amount of each data slice. We adjust the threshold based on the average number of new links in new data slices.
In summary, threshold settings help to balance the accuracy and efficiency of the ICP method in OSNs, which deserves more attention to carefully adjust in real applications.
8.2 Conclusion
In order to promote the wide use of the ICP in OSNs and improve its accuracy while ensuring efficiency, we focus on the cumulative error reduction of ICP in different OSN applications. We first identity and study two types of errors, the cumulative reconstruction error and the prediction error, and propose two optimal optimization problems based on these two errors. We then propose several general restarting strategies to address the cumulative error reduction problems, and we deeply differentiate their features and suitable scenarios. Finally, we apply our restarting strategies in three typical OSN applications and we conduct extensive experiments to verify the effectiveness.
In future work, we would like to combine multiple restarting strategies and propose an adaptive hybrid restarting framework. We are also interested in dynamically adjusting the thresholds of different strategies.
REFERENCES
- 2018. Behance.net social network. Retrieved from http://www.behance.net/.
- Evrim Acar, Daniel M. Dunlavy, and Tamara G. Kolda. 2009. Link prediction on evolving data using matrix and tensor factorizations. In Proceedings of the 2009 IEEE International Conference on Data Mining Workshops. IEEE, 262–269.
- Mohammad Al Hasan and Mohammed J. Zaki. 2011. A survey of link prediction in social networks. In Social Network Data Analytics. Springer, 243–275.
- Peng Bao, Hua-Wei Shen, Junming Huang, and Xue Qi Cheng. 2013. Popularity prediction in microblogging network: A case study on sina weibo. In Proceedings of the 22nd International Conference on World Wide Web. ACM, 177–178.
- Qi Cao, Huawei Shen, Hao Gao, Jinhua Gao, and Xueqi Cheng. 2017. Predicting the popularity of online content with group-specific models. Communications of the ACM 53, 8 (2017), 80–88.
- Chen Chen and Hanghang Tong. 2015. Fast eigen-functions tracking on dynamic graphs. In Proceedings of the 2015 SIAM International Conference on Data Mining.
- Yunqi Dong and Wenjun Jiang. 2019. Brand purchase prediction based on time-evolving user behaviors in e-commerce. Concurrency and Computation: Practice and Experience 31, 1 (2019), e4882.
- Daniel M. Dunlavy, Tamara G. Kolda, and Evrim Acar. 2011. Temporal link prediction using matrix and tensor factorizations. ACM Trans Knowledge Discovery from Data 5, 2 (2011), 1–27.
- Ye Yuan, Guy-Bart Stan, Sean Warnick, and Jorge Goncalves. 2011. Robust dynamical network structure reconstruction. Automatica 47, 6 (2011), 1230--1235
- Ziwei Zhang, Peng Cui, Jian Pei, XiaoWang, and Wenwu Zhu. 2018. TIMERS: Error-bounded SVD restart on dynamic networks. Proceedings of the 32nd AAAI Conference on Artificial Intelligence 32, 1 (2018), 224--231.
- Sheng Gao, Ludovic Denoyer, and Patrick Gallinari. 2011. Link pattern prediction with tensor decomposition in multi-relational networks. In Proceedings of the 2011 IEEE Symposium on Computational Intelligence and Data Mining. IEEE, 333–340.
- Sheng Gao, Ludovic Denoyer, and Patrick Gallinari. 2011. Temporal link prediction by integrating content and structure information. In Proceedings of the 20th ACM International Conference on Information and Knowledge Management. ACM, 1169–1174.
- Xiaofeng Gao, Zhenhao Cao, Sha Li, Bin Yao, Guihai Chen, and Shaojie Tang. 2019. Taxonomy and evaluation for microblog popularity prediction. ACM Transactions on Knowledge Discovery from Data 13, 2 (2019), 15.
- Hancheng Ge, James Caverlee, and Haokai Lu. 2016. TAPER: A contextual tensor-based approach for personalized expert recommendation. In Proceedings of the 10th ACM Conference on Recommender Systems. ACM, 261–268.
- Lars Grasedyck, Daniel Kressner, and Christine Tobler. 2013. A literature survey of low-rank tensor approximation techniques. GAMM-Mitteilungen 36, 1 (2013), 53–78.
- Ekta Gujral, Ravdeep Pasricha, and Evangelos E. Papalexakis. 2018. Sambaten: Sampling-based batch incremental tensor decomposition. In Proceedings of the 2018 SIAM International Conference on Data Mining. SIAM, 387–395.
- Johan Håstad. 1990. Tensor rank is NP-complete. Journal of Algorithms 11, 4 (1990), 644–654.
- Laurent Hébert-Dufresne, Joshua A. Grochow, and Antoine Allard. 2016. Multi-scale structure and topological anomaly detection via a new network statistic: The onion decomposition. Scientific Reports 6, 1 (2016), 1--9.
- Minh X. Hoang, Xuan-Hong Dang, Xiang Wu, Zhenyu Yan, and Ambuj K. Singh. 2017. GPOP: Scalable group-level popularity prediction for online content in social networks. In Proceedings of the 26th International Conference on World Wide Web. 725–733.
- Chunli Huang, Wenjun Jiang, Jie Wu, and Guojun Wang. 2020. Personalized review recommendation based on users’ aspect sentiment. ACM Transactions on Internet Technology 20, 4 (2020), 1--26.
- Junming Huang, Chao Li, Wen-Qiang Wang, Hua-Wei Shen, Guojie Li, and Xue-Qi Cheng. 2014. Temporal scaling in information propagation. Scientific Reports 4, 1 (2014), 1--6.
- Wenjun Jiang, Guojun Wang, Md Zakirul Alam Bhuiyan, and Jie Wu. 2016. Understanding graph-based trust evaluation in online social networks: Methodologies and challenges. ACM Computing Surveys 49, 1 (
May 2016), 10:1--10:35. - W. Jiang, J. Wu, G. Wang, and H. Zheng. 2016. Forming opinions via trusted friends: Time-evolving rating prediction using fluid dynamics. IEEE Transactions on Computers 65, 4 (2016), 1211–1224.
- George Karypis and Vipin Kumar. 1998. Multilevel k-way partitioning scheme for irregular graphs. Journal of Parallel and Distributed computing 48, 1 (1998), 96–129.
- Tamara G. Kolda and Brett W. Bader. 2009. Tensor decompositions and applications. SIAM Review 51, 3 (2009), 455–500.
- Jérôme Kunegis and Andreas Lommatzsch. 2009. Learning spectral graph transformations for link prediction. In Proceedings of the 26th Annual International Conference on Machine Learning.
- Haewoon Kwak, Changhyun Lee, Hosung Park, and Sue Moon. 2010. What is Twitter, a social network or a news media?. In Proceedings of the 19th International Conference on World Wide Web. ACM, 591–600.
- Kristina Lerman and Tad Hogg. 2010. Using a model of social dynamics to predict popularity of news. In Proceedings of the 19th International Conference on World Wide Web.
- Norman Levinson. 1946. The Wiener (root mean square) error criterion in filter design and prediction. Journal of Mathematics and Physics 25, 1–4 (1946), 261–278.
- Shiou-Chi Li, Yu-Hao Ke, Fa-Yuan Liu, and Jen-Wei Huang. 2015. Reconstructing dynamic social network by choosing local maximum degree substitute. In Proceedings of the 2015 IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining. ACM, 1604–1605.
- Jin Xiaojie Zhang Luming Xu Xianghua Yan Shuicheng Li Ping, Feng Jiashi. 2017. Online robust low-rank tensor learning ping. In Proceedings of the 26th International Joint Conference on Artificial Intelligence. 2180–2186.
- David Liben-Nowell and Jon Kleinberg. 2007. The link-prediction problem for social networks. Journal of the American Society for Information Science and Technology 58, 7 (2007), 1019–1031.
- Linyuan Lü and Tao Zhou. 2011. Link prediction in complex networks: A survey. Physica A: Statistical Mechanics and Its Applications 390, 6 (2011), 1150–1170.
- Víctor Martínez, Fernando Berzal, and Juan-Carlos Cubero. 2017. A survey of link prediction in complex networks. ACM Computing Surveys 49, 4 (2017), 69.
- Aditya Krishna Menon and Charles Elkan. 2011. Link prediction via matrix factorization. In Proceedings of the Joint European Conference on Machine Learning and Knowledge Discovery in Databases. Springer, 437–452.
- Elisa Mussumeci and Flávio Codeço Coelho. 2018. Reconstructing news spread networks and studying its dynamics. Social Network Analysis and Mining 8, 1 (2018), 6.
- Mingdong Ou, Peng Cui, Jian Pei, Ziwei Zhang, and Wenwu Zhu. 2016. Asymmetric transitivity preserving graph embedding. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. ACM, 1105–1114.
- Evangelos E. Papalexakis, Christos Faloutsos, and Nicholas D. Sidiropoulos. 2017. Tensors for data mining and data fusion: Models, applications, and scalable algorithms. ACM Transactions on Intelligent Systems and Technology 8, 2 (2017), 16.
- Ashwin Paranjape, Austin R. Benson, and Jure Leskovec. 2017. Motifs in temporal networks. In Proceedings of the 10th ACM International Conference on Web Search and Data Mining. ACM.
- Tiago P. Peixoto. 2019. Network reconstruction and community detection from dynamics. Physical Review Letters 123, 12 (2019), 128301.
- Henrique Pinto, Jussara M. Almeida, and Marcos A. Gonçalves. 2013. Using early view patterns to predict the popularity of Youtube videos. In Proceedings of the 2013 ACM International Conference on Web Search and Data Mining. ACM, 365–374.
- Justin Ruths and Derek Ruths. 2014. Control profiles of complex networks. Science 343, 6177 (2014), 1373–1376.
- Nigel Swain. 2010. Patterns and dynamics of users’ behavior and interaction: Network analysis of an online community.Journal of the Association for Information Science and Technology 60, 5 (2010), 911–932.
- Gabor Szabo and B. A. Huberman. 2010. Predicting the popularity of online content. Communications of the ACM 53, 8 (2010), 80--88.
- Alexandru Tatar, Panayotis Antoniadis, Marcelo Dias De Amorim, and Serge Fdida. 2014. From popularity prediction to ranking online news. Social Network Analysis and Mining 4, 1 (2014), 174.
- Alexandru Tatar, Marcelo Dias De Amorim, Serge Fdida, and Panayotis Antoniadis. 2014. A survey on predicting the popularity of web content. Journal of Internet Services and Applications 5, 1 (2014), 8.
- Alexandru Tatar, Jérémie Leguay, Panayotis Antoniadis, Arnaud Limbourg, Marcelo Dias de Amorim, and Serge Fdida. 2011. Predicting the popularity of online articles based on user comments. In Proceedings of the International Conference on Web Intelligence, Mining and Semantics. ACM, 67.
- Chao Wang, V. Satuluri, and S. Parthasarathy. 2007. Local probabilistic models for link prediction. In Proceedings of the 7th IEEE International Conference on Data Mining.
- Feng Wang, Jinhua She, Yasuhiro Ohyama, Wenjun Jiang, Geyong Min, Guojun Wang, and Min Wu. 2021. Maximizing positive influence in competitive social networks: A trust-based solution. Information Sciences 546 (2021), 559–572. DOI: https://doi.org/10.1016/j.ins.2020.09.002
- Jingjing Wang, Wenjun Jiang, and Guojun Wang. 2021. Incremental group-level popularity prediction in online social networks. Work in Progress (2021).
- Peng Wang, BaoWen Xu, YuRong Wu, and XiaoYu Zhou. 2015. Link prediction in social networks: The state-of-the-art. Science China Information Sciences 58, 1 (2015), 1–38.
- Xian Wu, Baoxu Shi, Yuxiao Dong, Chao Huang, and Nitesh V. Chawla. 2019. Neural tensor factorization for temporal interaction learning. In Proceedings of the 12th ACM International Conference on Web Search and Data Mining. ACM, 537–545.
- Peike Xia, Wenjun Jiang, Jie Wu, Surong Xiao, and Guojun Wang. 2020. Exploiting temporal dynamics in product reviews for dynamic sentiment prediction at the aspect level. ACM Transactions on Knowledge Discovery from Data 1, 1, Article 1 (2021), 27 pages. https://doi.org/10.1145/3441451
- Jie Xu, Mihaela Van Der Schaar, Jiangchuan Liu, and Haitao Li. 2015. Forecasting popularity of videos using social media. IEEE Journal of Selected Topics in Signal Processing 9, 2 (2015), 330–343.
- Jie Xu, Mihaela Van Der Schaar, Jiangchuan Liu, and Haitao Li. 2015. Timely video popularity forecasting based on social networks. In Proceedings of the 2015 IEEE Conference on Computer Communications. IEEE, 2308–2316.
- Jaewon Yang and Jure Leskovec. 2011. Patterns of temporal variation in online media. In Proceedings of the 4th ACM International Conference on Web Search and Data Mining. ACM, 177–186.
- Enoch Yeung, Jongmin Kim, Jorge Gonçalves, and Richard M. Murray. 2015. Global network identification from reconstructed dynamical structure subnetworks: Applications to biochemical reaction networks. In Proceedings of the 2015 54th IEEE Conference on Decision and Control. IEEE.
- Jifeng Zhang, Wenjun Jiang, Jinrui Zhang, Jie Wu, and Guojun Wang. 2021. Exploring weather data to predict activity attendance in event-based social network: From the organizer's view. ACM Transactions on the Web 1, 1, Article 1 (2021), 25 pages. https://doi.org/10.1145/3440134
- Shuo Zhou, S. Erfani, and J. Bailey. 2018. Online CP Decomposition for Sparse Tensors. In Proceedings of the 2018 IEEE International Conference on Data Mining. IEEE Computer Society.
- Shuo Zhou, Nguyen Xuan Vinh, James Bailey, Yunzhe Jia, and Ian Davidson. 2016. Accelerating online CP decompositions for higher order tensors. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. 1375–1384.
- Linhong Zhu, Dong Guo, Junming Yin, Greg Ver Steeg, and Aram Galstyan. 2016. Scalable temporal latent space inference for link prediction in dynamic social networks. IEEE Transactions on Knowledge and Data Engineering 28, 10 (2016), 2765–2777.
Footnotes
- 1 https://www.domo.com/learn/data-never-sleeps-7.
- 2 http://cs.ucsb.edu/∼mhoang/gpop.tar.gz.
- 3 http://snap.stanford.edu/data/sx-mathoverflow.html.
- 4 http://snap.stanford.edu/data/CollegeMsg.html.
- 5 http://snap.stanford.edu/data/sx-mathoverflow.html.
- 6 http://cs.ucsb.edu/∼mhoang/gpop.tar.gz.
- 7 http://cs.ucsb.edu/∼mhoang/gpop.tar.gz.
This research was supported by NSFC Grant (61632009), Guangdong Provincial NSF Grant (2017A030308006), Open Project of Zhejiang Lab (2019KE0AB02), the China Scholarships Council (Grant No. 201906130131), the Science and Technology Program of Changsha City (kq 2004017), and in part by NSF Grants (CNS 1824440, CNS 1828363, CNS 1757533, CNS 1618398, CNS 1651947, and CNS 1564128), the National Outstanding Youth Science Program of NSFC Grant (61625202), and NSFC Grant (61872127).
Authors’ addresses: J. Wang, W. Jiang (corresponding author), and K. Li, Hunan University, College of Computer Science and Electronic Engineering, Lushan South Road, Yuelu District, Changsha City, Hunan Province, 410082, China; emails: [email protected], [email protected], [email protected]; K. Li, Hunan University, College of Computer Science and Electronic Engineering, Lushan South Road, Yuelu District, Changsha City, Hunan Province, 410082, China and State University of New York, Department of Computer Science, New Paltz, New York, 12561, USA; email: [email protected].
Permission to make digital or hard copies of all or part of this work for personal or classroom use is granted without fee provided that copies are not made or distributed for profit or commercial advantage and that copies bear this notice and the full citation on the first page. Copyrights for components of this work owned by others than ACM must be honored. Abstracting with credit is permitted. To copy otherwise, or republish, to post on servers or to redistribute to lists, requires prior specific permission and/or a fee. Request permissions from [email protected].
©2021 Association for Computing Machinery.
1556-4681/2021/04-ART42 $15.00
DOI: https://doi.org/10.1145/3441645
Publication History: Received October 2019; revised November 2020; accepted December 2020