Abstract
We address the challenging problem of whole slide image (WSI) classification. WSIs have very high resolutions and usually lack localized annotations. WSI classification can be cast as a multiple instance learning (MIL) problem when only slide-level labels are available. We propose a MIL-based method for WSI classification and tumor detection that does not require localized annotations. Our method has three major components. First, we introduce a novel MIL aggregator that models the relations of the instances in a dual-stream architecture with trainable distance measurement. Second, since WSIs can produce large or unbalanced bags that hinder the training of MIL models, we propose to use self-supervised contrastive learning to extract good representations for MIL and alleviate the issue of prohibitive memory cost for large bags. Third, we adopt a pyramidal fusion mechanism for multiscale WSI features, and further improve the accuracy of classification and localization. Our model is evaluated on two representative WSI datasets. The classification accuracy of our model compares favorably to fully-supervised methods, with less than 2% accuracy gap across datasets. Our results also outperform all previous MIL-based methods. Additional benchmark results on standard MIL datasets further demonstrate the superior performance of our MIL aggregator on general MIL problems.
1. Introduction
Whole slide scanning is a powerful and widely used tool to visualize tissue sections in disease diagnosis, medical education, and pathological research [10, 38]. The scanning converts tissues on glass slides into digital whole slide images (WSIs) for assessment, sharing, and analysis. Automated disease detection in WSIs has been a long-standing challenge for computer aided diagnostic systems. We have begun to see some recent success from computer vision and medical image analysis communities [6, 44, 3, 24, 27, 29], fueled by the advances in deep learning.
WSIs have extremely high resolutions — a typical pathology image has a size of 40, 000 × 40, 000. Consequently, the most widely used paradigm for WSI classification is patch-based processing — a WSI is divided into thousands of small patches and further examined by a classifier e.g., a convolutional neural network (CNN) [21, 53, 35, 11, 33]. In clinics, a disease-positive tissue section might only take a small portion (e.g., less than 20%) of the whole tissue, leading to a large number of disease-negative patches. Unfortunately, with gigapixel resolution, patch-level labeling by expert pathologists is very time consuming and difficult to scale. To address this challenge, several recent studies [21, 3, 18] have demonstrated the promise of weakly supervised WSI classification, where only slide-level labels are used to train a patch-based classifier.
The majority of previous approaches [21, 53, 35, 11, 18, 8] on weakly supervised WSI classification follows a multiple instance learning (MIL) problem formulation [14, 34], where each WSI is considered as a bag that contains many instances of patches. A WSI (bag) is labeled as disease-positive if any of its patches (instances) is disease-positive (e.g., with lesions). Patch-level features or scores are extracted, aggregated, and examined by a classifier that predicts slide-level labels. Recent MIL based approaches have greatly benefited from using deep neural networks for feature extraction and feature aggregation [22, 50, 37].
Two major challenges exist in developing deep MIL models for weakly supervised WSI classification. First, when patches (instances) in positive images (bags) are highly unbalanced, i.e., only a small portion of patches are positive, the models are likely to misclassify those positive instances [22] when using a simple aggregation operation, such as the widely adopted max-pooling. This is because, under the assumptions of MIL, max-pooling can lead to a shift of the decision boundary compared to fully-supervised training (Figure 1). Besides, the model can easily suffer from overfitting and unable to learn rich feature representations due to the weak supervisory signal [12, 32,1]. Second, current models either use fixed patch features extracted by a CNN or only update the feature extractor using a few high score patches, as the end-to-end training of the feature extractor and aggregator is prohibitively expensive for large bags [12, 3, 32]. Such a simplified learning scheme might lead to sub-optimal patch features for WSI classification.
Figure 1.

Decision boundary learned in MIL. Left: Max pooling delineates the decision boundary according to the highest-score instances in each bag. Right: DSMIL measures the distance between each instance and the highest-score instance.
To address these challenges, we propose a novel deep MIL model, dubbed dual-stream multiple instance learning network (DSMIL). Specifically, DSMIL jointly learns a patch (instance) and an image (bag) classifier, using a two-stream architecture. The first stream deploys a standard max-pooling to identify the highest scored instance (referred to as critical instance), while the second stream computes an attention score for each instance by measuring its distance to the critical instance. DSMIL further applies a soft selection of instances using the attention scores, leading to a decision boundary that better delineates the instances in positive bags, as shown in Figure 1. Importantly, DSMIL makes use of self-supervised contrastive learning for training the feature extractor for WSI, producing strong patch representations. In addition, DSMIL incorporates a multiscale feature fusion mechanism that can leverage tissue features ranging from millimeter-scale (e.g., vessels and glands) to cellular-scale (tissue microenvironment).
We evaluate DSMIL for weakly supervised WSI classification on two public WSI datasets including Camelyon16 and TCGA lung cancer. The results show that DSMIL outperforms other recent MIL models in classification accuracy by at least 2.3%. More importantly, our classification accuracy compares favorably to fully-supervised methods, with less than 2% accuracy gap. Moreover, DSMIL also has superior localization accuracy, outperforming previous MIL models by a significant margin. Finally, we demonstrate the state-of-the-art performance of DSMIL on general MIL problems beyond weakly supervised WSI classification.
2. Related Work
Our work develops MIL for WSI analysis using deep models. MIL itself is a well-established topic. We refer the readers to [4] for a survey. In this section, we briefly review recent efforts on deep MIL models, as well as relevant works on MIL models for WSI analysis.
Deep MIL Models.
Conventionally, MIL models consider handcrafted aggregators, such as mean-pooling and max-pooling [16, 39]. Recently, it is shown that parameterizing the aggregation operator with neural networks can still be beneficial [16, 52, 37]. Ilse et al. [22] proposed an attention-based aggregation operator parameterized by neural networks which includes the contribution of each instance to the bag embedding. Methods that consider the contextual information are proposed to model the dependencies between the instances such as graph neural network-based approaches and capsule network-based approaches [47, 55, 8].
We deploy a non-local operation to model the instance-to-instance and instance-to-bag relations [51]. Differing from the attention mechanism in attention-based MIL (AB-MIL) [22], the attentions in our model are explicitly computed based on a trainable distance measurement. Our method is also different from graph models and capsule networks in that the weights between the nodes are functions of the two nodes instead of learned parameters [43, 42]. The measurement mechanism is similar to self-attention [48, 51], but differs in that the measurement is done only between one node (the critical instance) to the others. Our dual-stream non-local operation also differs from asymmetric non-local operation in that the embeddings are filtered according to the confidence scores learned in a separate branch, instead of on the embeddings [56]. In addition, deep MIL models have been considered for other weakly supervised vision tasks, including weakly supervised object localization [9] and detection [45, 49]. In this paper, we focus on weakly supervised classification of WSI.
MIL Models for WSI Analysis.
MIL has been successfully applied to WSI analysis for tasks such as cell segmentation and tumor detection [54, 21, 40, 23, 3, 8]. Campanella et al. [3] show that a MIL classifier trained on large weakly-labeled WSI datasets generalizes better than a fully-supervised classifier trained on pixel-level-annotated small lab datasets. The former is easy to obtain on large scale from everyday clinics while the latter requires labor-intensive annotations in research labs.
Training a CNN for good feature representations in MIL is non-trivial for WSI analysis, due to the prohibitive memory requirement and the noisy supervisory signal [32, 12]. Recently, semi-supervised learning has been used to enable the training of the classifier for WSI classification with limited patch-level labels [26]. In contrast, our work makes use of self-supervised contrastive learning [7] for feature extraction in MIL. Self-supervised contrastive learning has demonstrated success in learning visual representations [36, 7, 19], yet remains unexplored in WSI analysis.
The assessment of WSIs by pathologists is done in multiscale [2, 17, 46] and it is common to consider multiscale features in WSI analysis. Using bags that simply include features from different magnifications of WSI in MIL has shown to be beneficial [18]. Another possibility [33] is to select regions at low-magnification and further zoom in these regions for high-magnification patches. Our multiscale feature analysis strategy is inspired by previous works on multiscale feature representation using deep models [41, 28], yet simultaneously benefits our DSMIL model for the ability to locally-constrain the patch attentions.
3. Method
We now present our method for weakly supervised WSI classification. This section introduces the formulation of MIL and presents our model — DSMIL.
3.1. Background: MIL Formulation
In MIL, a group of training samples is considered as a bag containing multiple instances. Each bag has a bag label that is positive if the bag contains at least one positive instance and negative if it contains no such positive instance. The instance-level labels are unknown. In the case of binary classification, let B = {(x1, y1), …, (xn, yn)} be a bag where xi ∈ χ are instances with labels yi ∈ {0, 1}, the label of B is given by
| (1) |
MIL further uses a suitable transformation f and a permutation-invariant transformation g [22, 5] to predict the label of B, given by
| (2) |
Multiple instance learning could be modeled in two ways based on the choices of f and g: 1) Instance-based approach. f is an instance classifier that scores each instance, g is a pooling operator that aggregates the instance scores to produce a bag score. 2) Embedding-based approach. f is an instance-level feature extractor that maps each instance to an embedding, g is an aggregation operator that produces a bag embedding from the instance embeddings and outputs a bag score based on the bag embedding. The embedding-based method produces a bag score based on a bag embedding directly supervised by the bag label and usually yields better accuracy compared to the instance-based method [52], however, it is usually harder to determine the key instances that trigger the classifier [30].
In the setting of weakly supervised WSI classification, each WSI is considered as a bag and the patches extracted from it are considered as the instances of this bag. We will then describe our model that jointly learns a instance-level classifier as well as an embedding aggregator and explain how such hybrid architecture could provide advantages of both the instance-based and embedding-based methods.
3.2. DSMIL for WSI Classification
Our key innovations are the design of a novel aggregation function g, and the learning of the feature extractor f. Specifically, we propose DSMIL that consists of a masked non-local block and a max-pooling block for feature aggregation, with input instance embeddings learned by self-supervised contrastive learning. Moreover, DSMIL combines multiscale embeddings using a pyramidal strategy, and thus ensures the local constraints of the attentions for patches in a WSI. Figure 2 presents an overview of our DSMIL. We now describe each component of DSMIL.
Figure 2.

Overview of our DSMIL. Patches extracted from each magnification of the WSIs are used for self-supervised contrastive learning separately. The trained feature extractors are used to compute embeddings of patches. Embeddings of different scales of a WSI are concatenated to form feature pyramids to train the MIL aggregator. The figure shows an example of two magnifications (20× and 5×). The 5× feature vector is duplicated and concatenated with each of the 20× feature vectors of the sub-images within this 5× patch.
MIL Aggregator with Masked Non-Local Operation.
In contrast to most previous methods that either learn an instance classifier or a bag classifier, DSMIL jointly learns the instance classifier and the bag classifier as well as the bag embedding in a dual-stream architecture.
Let B = {x1, …, xn} denote a bag of patches of a WSI. Given a feature extractor f, each instance xi can be projected into an embedding . The first stream uses an instance classifier on each instance embedding, followed by max-pooling on the scores:
| (3) |
where W0 is a weight vector. The max-pooling stream determines the instance with the highest score (critical instance). Max-pooling is a permutation-invariant operation, thus, this stream satisfies equation 2.
The second stream aggregates the above instance embeddings into a bag embedding which is further scored by a bag classifier. We obtain the embedding hm of the critical instance, and transform each instance embedding hi (including hm) into two vectors, query and information , which are given respectively by:
| (4) |
where Wq and Wv each is a weight matrix. We then define a distance measurement U between an arbitrary instance to the critical instance as:
| (5) |
”〈·, ·〉” denotes the inner product of two vectors. The bag embedding b is the weighted element-wise sum of the information vectors vi of all instances, using the distances to the critical instance as the weights:
| (6) |
The bag score cb is then given by:
| (7) |
where Wb is a weight vector for binary classification. This operation is similar to self-attention [48]. but differs in that the query-key matching is performed only between the critical node and the other nodes (including the critical node itself). Moreover, instead of matching each query with additional key vectors like self-attention, the query is matched with other queries and no key vector is learned.
The dot product measures the similarity between two queries, resulting in larger values for instances that are more similar. Therefore, instances more similar to the critical instance will have greater attention weights. The additional layer for the information vectors vi allows contributing information to be extracted within each instance. The soft-max operation in Equation 5 ensures the attention weights are summed to 1 regardless of the bag size.
Since the critical instance does not depend on the order of the instances and the measurement U is symmetric, this sum term so as the bag embedding b does not depend on the order of the instances, thus, the second stream is permutation-invariant and satisfies Equation 2. The final bag score is the average of the scores of the two streams:
| (8) |
Note that DSMIL can handle the case of multi-class MIL problems by max-pooling the instance scores and compute attention weights for each class separately. The result bag embedding is then a matrix where C is the number of classes, with each entry a weighted sum of the instance information vectors vi. The last fully connected layer will then have an output channel number of C.
The information vector vi allows intra-instance feature selection while the distance measurement applies an inter-instance selection according to the similarity to the critical instance. The resulted bag embedding has a constant shape regardless of the bag size, and will be used to compute the output bag score cb at inference time. The architecture of the aggregator is illustrated in Figure 3.
Figure 3.

MIL aggregator of DSMIL. The max-pooling branch determines the critical instance by pooling the instance scores. The aggregation branch measures the distance between each instance to the critical instance and produces a bag embedding by summing the instance embeddings using the distances as weights. Scores of the two streams are averaged to produce the final score.
Self-Supervised Contrastive Learning of WSI Features.
Moving beyond the aggregation operation, we propose to use self-supervised contrastive learning for learning the feature extractor f. Specifically, we consider SimCLR from [7], a state-of-the-art self-supervised learning framework that enables robust representations to be learned without the need for manual labels. SimCLR deploys a contrastive learning strategy that trains the CNN to associate the sub-images from the same image in a batch of sub-images. The sub-images are randomly selected in a batch of images and fed into two random image augmentation branches. The model is trained to maximize the agreement between the sub-images that are from the same image using a contrastive loss. After the training converges, the feature extractor is kept and used to compute the representations of the training samples for downstream tasks. The datasets used for SimCLR consist of patches extracted from the WSIs. The patches are densely cropped without overlap and treated as individual images for SimCLR training.
Locally-Constrained Multiscale Attention.
Finally, we make use of a pyramidal concatenation strategy to integrate features of WSIs from different magnifications. First, For each low-magnification patch, we obtain the feature vector of this patch as well as the feature vectors of the sub-images in the higher magnification within this patch. For example, a patch with a size of 224×224 at 10× magnification will contain 4 sub-images with a size of 224×224 at 20× magnification. For every 10× patch, we then concatenate the 10× feature vector with each of the 20× features and obtain 4 feature vectors. Figure 4 illustrates the case of three magnifications (20×−10×−5×). We demonstrate the effectiveness of this method using features from two magnifications (20× and 5×) in the experiment, but the idea is general and can be extended to more magnifications.
Figure 4.
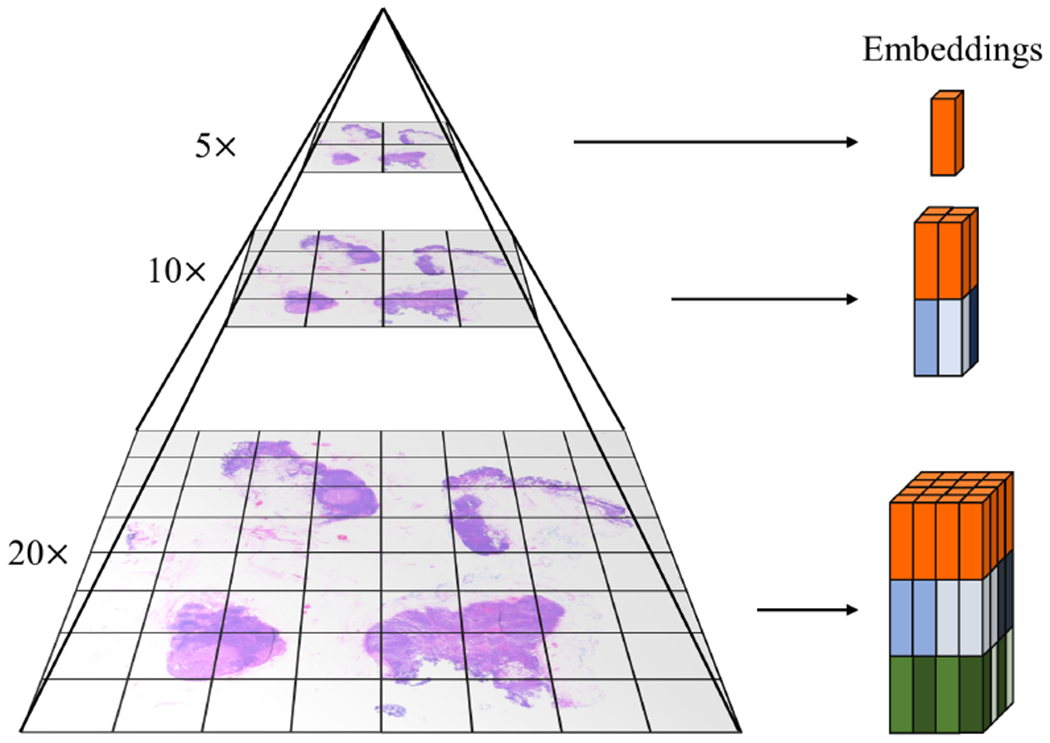
Pyramidal concatenation of multiscale features in WSI. Feature vector from a lower magnification patch is duplicated and concatenated to feature vectors of its higher magnification patches.
There are two major benefits of this concatenation method: 1) The first part of the resulted feature vector is the same for the 20× patches that belong to the same 5× patch. As a result, in DSMIL, the distance measurement results si = 〈qi, qm〉 for these vectors will tend to be similar and the instances will be assigned similar attention weights. The second part of the feature vector is specific to each 20× patch which allows the attention weights to vary among these patches. 2) The information from different scales are preserved in the feature vectors, allowing the network to select the appropriate information vi across different scales.
4. Experiments and Results
We now present our experiments and results. First, we report results on two clinical WSI datasets, Camelyon16 and TCGA lung cancer, that cover the cases of unbalanced/balanced bags and single/multiple class MIL problems. Moreover, we present an ablation study, demonstrating the effectiveness of our MIL aggregator, the contrastive feature learning, and the multiscale attention mechanism.
Experiment Setup and Evaluation Metrics.
We report the accuracy and area under the curve (AUC) scores of DSMIL for the task of WSI classification on both datasets. On Camelyon16, we also evaluate localization performance by reporting free response operating characteristic curves (FROC) [15]. To pre-process the WSIs datasets, every WSI is cropped into 224 × 224 patches without overlap to form a bag, in the magnifications of 20× and 5×. Background patches (entropy < 5) are discarded. Constantly better results are obtained on 20× images for both datasets and are reported for experiments using a single-scale of WSI.
Implementation Details.
We use Adam [25] optimizer with a constant learning rate of 0.0001 to update the model weights during the training. The mini-batch size for training MIL models is 1 (bag). Patches extracted from the training sets of the WSI datasets are used to train the feature extractor using SimCLR. For SimCLR, we use Adam optimizer with an initial learning rate of 0.0001, a cosine annealing (without warm restarts) scheme for learning rate scheduling [31], and a min-batch size of 512. The CNN backbone used for MIL models and SimCLR is ResNet18 [20].
4.1. Results on Camelyon16
We first present our results on Camelyon16. We introduce the dataset and baselines, and discuss our results on both classification and localization.
Dataset.
Camelyon16 is a public dataset proposed for metastasis detection in breast cancer [15]. The dataset consists of 271 training images and 129 testing images, which yield roughly 3.2 million patches at 20× magnification and 0.25 million patches at 5× magnification with on average about 8,000 and 625 patches per bag. Tumor regions are fully labeled with pixel-level annotations on each slide. We ignore the pixel-level annotations in the training and consider only slide-level labels (i.e. the slide is considered positive if it contains any annotated tumor regions). The resulted bags contain mixtures of tumor and healthy patches for positive bags and all healthy patches for negative bags.
The positive bags in this dataset are highly unbalanced. Only a small portion of regions in a positive slide contains tumor (roughly <10% of the total tissue area per slide) which leads to a large portion of negative patches in a positive bag. This makes it hard for good representations to be directly learned in most MIL models [32, 12]. We show that our method relying on only the slide-level labels can overcome this difficulty and achieves performance comparable to fully-supervised methods that use the pixel-level labels.
Baselines.
We evaluate and compare DSMIL to a strong set of baselines, including (1) deep models using traditional MIL pooling operators such as max-pooling and mean-pooling and (2) recent deep MIL models [18, 3, 22], on the tasks of WSI classification and tumor localization. Moreover, we obtain an upper-bound fully-supervised model by making use of the pixel-level annotations, where a patch is labeled positive if it falls within a tumor region and the score of a WSI is then obtained by averaging the scores of all its patches in testing. Results on the classification task can demonstrate the efficacy of our model in terms of producing good bag embeddings, while results on the localization task can demonstrate the capability of DSMIL to delineate positive instances in positive bags.
Classification Results.
The classification results are summarized in Table 1. Features are learned using self-supervised contrastive learning on the 20× patches under the same settings. The contribution of using self-supervised contrastive learning will be presented in the ablation study. The results suggest that, though both better than traditional pooling operators, DSMIL achieves better aggregation than ABMIL which implements no additional regularization on the learned attentions, with about 2.6% improvements in classification on the single scale setting. The recurrent neural network-based model without considering the permutation-invariant characteristics does not outperform the traditional pooling operators. With the multiscale attention mechanism integrated, DSMIL achieves improved results matching the performance of the fully-supervised method, with a classification accuracy gap smaller than 2%.
Table 1.
Results on Camelyon16 dataset. DSMIL/DSMIL-LC denote our model with/without the proposed multiscale attention mechanism. Instance embeddings are produced by the feature extractor trained using SimCLR for all MIL models.
| Model | Scale | Classification | Localization | |
|---|---|---|---|---|
| Accuracy | AUC | FROC | ||
| Mean-pooling | Single | 0.7984 | 0.7620 | 0.1162 |
| Max-pooling | Single | 0.8295 | 0.8641 | 0.3313 |
| MILRNN [3] | Single | 0.8062 | 0.8064 | 0.3048 |
| ABMIL [22] | Single | 0.8450 | 0.8653 | 0.4056 |
| DSMIL | Single | 0.8682 | 0.8944 | 0.4296 |
|
| ||||
| Fully-supervised | Single | 0.9147 | 0.9362 | 0.5254 |
|
| ||||
| MS-MILRNN [3] | Multiple | 0.8140 | 0.8371 | 0.2791 |
| MS-ABMIL [18] | Multiple | 0.8760 | 0.8872 | 0.4191 |
| DSMIL-LC | Multiple | 0.8992 | 0.9165 | 0.4371 |
Localization Results.
Pixel-level annotations are available for Camelyon16 which allow us to test the localization ability of our method. The localization performance indicates the MIL model’s capability to delineate positive instances. The reported FROC score is defined as the average sensitivity at 6 predefined false positive rates: 1/4, 1/2, 1, 2, 4, and 8 FPs per WSI. The result shows that DSMIL, where the attention scores are explicitly computed using a trainable distance measurement, better delineates the positive patches with at least 6% relative improvement compared to ABMIL in detection localization. Detection maps of representative samples from the testing set are illustrated in Figure 5.
Figure 5.

Tumor localization in WSI using different MIL models. (a) A WSI from Camelyon16 testing set. (b)-(e) zoomed in area in the orange box of (a). (b) Max-pooling. (c) ABMIL [22]. (d) DSMIL. (e) DSMIL-LC Note: for (b), classifier confidence scores are used for patch intensities; for (c) (d) and (e), attention weights are re-scaled from min-max to [0, 1] and used for patch intensities.
4.2. Results on TCGA Lung Cancer dataset
We further present our results on The Cancer Genome Atlas (TCGA) lung cancer dataset. We again introduce the dataset and discuss our results.
Dataset.
The WSIs include two sub-types of lung cancer, Lung Adenocarcinoma and Lung Squamous Cell Carcinoma, with in a total of 1054 diagnostic digital slides that can be downloaded from National Cancer Institute Data Portal. We randomly split the WSIs into 840 training slides and 210 testing slides (4 low-quality corrupted slides are discarded). The dataset yields 5.2 million patches at 20× magnification and 0.36 million patches at 5× magnification with in average about 5000 and 350 patches per bag. Only slide-level labels are available for this dataset.
The resulted bags contain mixtures of either type of tumor and healthy patches for positive bags, and all healthy patches for negative bags. Tumor slides in this dataset contain large portions of tumor regions (>80% per slide), leading to a large portion of positive patches in positive bags. Thus, training a classifier using a patch-based method without considering MIL already has reasonable results (i.e. treating the patches in a WSI as if they all have the same label as the whole WSI in training, and averaging the scores of the patches in a WSI in testing). We show that significantly improved results can be obtained by considering MIL.
Classification Results.
We compare both the features learned by SimCLR and by the patch-based method without considering MIL for this dataset. By contrast, the patch-based method does not converge for Camelyon16 due to the large number of negative patches in positive bags, so the patch-based features results are not included for Camelyon16. The results are summarized in Table 2 which suggests similar conclusions as Camelyon16 dataset.
Table 2.
Results on TCGA lung cancer dataset. Instance embeddings are produced by the feature extractor trained using SimCLR and patch-based method without considering MIL.
| SimCLR features | |||
|---|---|---|---|
|
| |||
| Model | Scale | Accuracy | AUC |
| Mean-pooling | Single | 0.8857 | 0.9369 |
| Max-pooling | Single | 0.8088 | 0.9014 |
| MIL-RNN [3] | Single | 0.8619 | 0.9107 |
| ABMIL [22] | Single | 0.9000 | 0.9488 |
| DSMIL | Single | 0.9190 | 0.9633 |
|
| |||
| MS-MIL-RNN [3] | Multiple | 0.8905 | 0.9213 |
| MS-ABMIL [18] | Multiple | 0.9000 | 0.9551 |
| DSMIL-LC | Multiple | 0.9286 | 0.9583 |
| Patch-based features | |||
|
| |||
| Model | Scale | Accuracy | AUC |
|
| |||
| Patch-based w/o MIL | Single | 0.8857 | 0.9506 |
|
| |||
| Mean-pooling | Single | 0.9096 | 0.9625 |
| Max-pooling | Single | 0.8286 | 0.8958 |
| MIL-RNN [3] | Single | 0.9048 | 0.9636 |
| ABMIL [22] | Single | 0.9381 | 0.9765 |
| DSMIL | Single | 0.9476 | 0.9809 |
|
| |||
| MS-MIL-RNN [3] | Multiple | 0.9096 | 0.9561 |
| MS-ABMIL [18] | Multiple | 0.9381 | 0.9792 |
| DSMIL-LC | Multiple | 0.9571 | 0.9815 |
4.3. Ablation Study
We now delineate the contributions of our model via ablation studies of the three major components of our model: DSMIL aggregator, self-supervised contrastive learning for the instance features, and the multiscale attention mechanism. We keep our DSMIL aggregator and compare features learned by different methods as well as different multiscale feature fusion methods for WSI. While the performance of our DSMIL aggregator has been demonstrated on two WSI datasets in the previous section, we further carry out extensive benchmark experiments for our MIL aggregator on several classical MIL datasets in the ablation study.
Effects of Contrastive Learning.
We compare the features learned by self-supervised contrastive learning to several baselines. 1) Use the feature extractor trained by max-pooling operator [3]. The end-to-end training using max-pooling can be done in a for-loop where the maximum-score instance is found dynamically and used to update the model weights without the need for large memory. 2) Use the feature extractor trained by the patch-based method without considering MIL (i.e. treating the patches in a WSI as if they all have the same label as the WSI in training, and averaging the scores of the patches in a WSI in testing). 3) Use the feature extractor pre-trained on ImageNet dataset [13].
The results are shown in Table 3. For unbalanced bags (e.g., Camelyon16 dataset), self-supervised contrastive learning leads to significantly better performance with at least 16% higher classification accuracy, even compared to the features obtained by end-to-end training of max-pooling. For balanced bags (e.g., TCGA lung cancer dataset), features learned by self-supervised contrastive learning are comparable to those of the patch-based method, yet are still significantly better (> 14% higher accuracy) than end-to-end training of max-pooling. Note that for unbalanced bags, the patch-based method does not lead to good features due to large amounts of negative samples in positive bags. Moreover, we further observe that using max-pooling on contrastive learning features also significantly outperforms the end-to-end training of max-pooling by about 10%. The results suggest that self-supervised contrastive learning is a feasible way to obtain good representations for MIL regardless of the distribution of negative and positive instances in the bags, and it also alleviates the memory requirement issue caused by large bag size.
Table 3.
Comparison of features learned by different methods for a fixed MIL aggregator.
| Dataset | Camelyon16 | TCGA | ||
|---|---|---|---|---|
|
| ||||
| Features | Accuracy | AUC | Accuracy | AUC |
| ImageNet | 0.6202 | 0.5408 | 0.7095 | 0.7260 |
| Max-pooling | 0.7099 | 0.7153 | 0.7714 | 0.8212 |
| Patch-based | 0.6977 | 0.5434 | 0.9476 | 0.9809 |
| Contrastive | 0.8682 | 0.8944 | 0.9190 | 0.9633 |
Effects of Multiscale Attention.
We further compare our multiscale attention mechanism to several other methods that consider multiscale WSI features, including 1) Concatenate the bag embeddings of the MIL model trained on each magnification before the fully-connected layer. 2) Use max-pooling on the predictions of the MIL model trained on each magnification [3]. 3) Mix the instances from different scales in a bag and feed the bag to the MIL model [18].
Table 4 presents the results on Camelyon16 dataset. Our multiscale attention outperforms the single scale approach by 3% and other multiscale approaches by at least 1.5%, suggesting that considering multiscale features could lead to better detection accuracy for WSI and structured multiscale features can further improve the results. Yet using two levels (5×+20×) produces better results than using all three levels (1.25×+5×+20×) with +1.6% in accuracy and +1.3% in AUC. We conjecture that sometimes information from a coarser scale (e.g. 1.25×) might not be as effective as a finer one (e.g. 20×), and the resulted vectors could become less discriminate. Thus, an attention mechanism along the magnification level might be needed to re-weight the features from different scales before fusion.
Table 4.
Comparison of different multiscale WSI feature integration methods. Multiscale approaches from other studies are used on our MIL aggregator with fixed instance embeddings learned by self-supervised contrastive learning on 20× and 5× WSI patches.
| Method | Accuracy | AUC |
|---|---|---|
| Single scale (20×) | 0.8682 | 0.8944 |
| Concatenation (5× + 20×) | 0.8682 | 0.8846 |
| Max Pooling (5× + 20×) | 0.8604 | 0.8731 |
| Mix (5× + 20×) | 0.8837 | 0.9097 |
|
| ||
| Ours (5× + 20×) | 0.8992 | 0.9165 |
| Ours (1.25× + 5× + 20×) | 0.8760 | 0.9034 |
DSMIL Aggregator on Other MIL Tasks.
Finally, We benchmark our dual-stream MIL aggregator on classical MIL benchmark datasets. These datasets consist of extracted feature vectors of the instances and do not require a feature extractor to be learned. The first two datasets (MUSK1, MUSK2) are used to predict drug effects based on the molecule conformations. A molecule can have different conformations and only some of them may be effective conformations [14]. Each bag contains multiple conformations of the same molecule, and the bag is labeled positive if at least one conformation is effective, negative otherwise. The other three datasets, ELEPHANT, FOX, and TIGER, consists of feature vectors extracted from images. Each bag includes a group of segments of an image and the bag is labeled as positive if at least one segment contains the animal of interest, negative if there is no such animal presented.
Since the feature vectors (instance embeddings) are already given, the experiment involves directly feeding the feature vectors to DSMIL aggregator. To test our MIL aggregator against other recent non-local architectures on MIL problem, we replace the proposed DSMIL aggregator with the non-local blocks in NL [51] (NLMIL) and ANL [56] (ANLMIL) and also evaluate their results across the 5 MIL datasets 5. Experiments are run 5 times each with a 10-fold cross-validation. The benchmark results show that our dual-stream MIL aggregator outperforms the previous best MIL models as well as other non-local operations such as NL and ANL by an average of 3% on general MIL problems.
5. Conclusion and Future Work
In this paper, we present a new MIL-based approach for weakly supervised WSI classification. Our method has demonstrated considerable improvement over previous methods on representative WSI datasets. Our key technical innovation is a novel MIL aggregator that outperforms recent MIL models on both MIL benchmark dataset and representative WSI datasets. We also propose to make use of self-supervised contrastive learning in MIL models and to incorporate multiscale features. Our method further integrates the proposed aggregator, contrastive learning, and multiscale features into a MIL model for WSI classification. By casting tumor detection in WSI as a MIL problem, our solution has the potential for real-world clinical applications where large amount of unannotated slides are available. We believe our work provides a solid step forward for both MIL and computational histopathology.
Future research includes designing self-supervised learning strategies that adapt to the characteristics of histopathological data. Moreover, mechanisms that model the spatial relations can be integrated to capture macroscale features in WSI that are spatially structured and could potentially lead to further improvement.
Table 5.
Performance comparison on classical MIL dataset. Experiments were run 5 times each with a 10-fold cross-validation. The mean and standard deviation of the classification accuracy is reported (mean ± std). mi-Net[52], MI-Net [52], MI-Net with DS [52], MI-Net with RC [52], ABMILP [22], ABMILP-Gated [22], GNN-MIL [47], DP-MINN [55]. NLMIL and ANLMIL use the non-local blocks from [51] and [56]. Previous benchmark results are taken from [22, 47, 55] and the same training setting as [22] is used.
| Methods | MUSK1 | MUSK2 | FOX | TIGER | ELEPHANT |
|---|---|---|---|---|---|
| mi-Net | 0.889 ± 0.039 | 0.858 ± 0.049 | 0.613 ± 0.035 | 0.824 ± 0.034 | 0.858 ± 0.037 |
| MI-Net | 0.887 ± 0.041 | 0.859 ± 0.046 | 0.622 ± 0.038 | 0.830 ± 0.032 | 0.862 ± 0.034 |
| MI-Net with DS | 0.894 ± 0.042 | 0.874 ± 0.043 | 0.630 ± 0.037 | 0.845 ± 0.039 | 0.872 ± 0.032 |
| MI-Net with RC | 0.898 ± 0.043 | 0.873 ± 0.044 | 0.619 ± 0.047 | 0.836 ± 0.037 | 0.857 ± 0.040 |
| ABMIL | 0.892 ± 0.040 | 0.858 ± 0.048 | 0.615 ± 0.043 | 0.839 ± 0.022 | 0.868 ± 0.022 |
| ABMIL-Gated | 0.900 ± 0.050 | 0.863 ± 0.042 | 0.603 ± 0.029 | 0.845 ± 0.018 | 0.857 ± 0.027 |
| GNN-MIL | 0.917 ± 0.048 | 0.892 ± 0.011 | 0.679 ± 0.007 | 0.876 ± 0.015 | 0.903 ± 0.010 |
| DP-MINN | 0.907 ± 0.036 | 0.926 ± 0.043 | 0.655 ± 0.052 | 0.897 ± 0.028 | 0.894 ± 0.030 |
|
| |||||
| NLMIL | 0.921 ± 0.017 | 0.910 ± 0.009 | 0.703 ± 0.035 | 0.857 ± 0.013 | 0.876 ± 0.011 |
| ANLMIL | 0.912 ± 0.009 | 0.822 ± 0.084 | 0.643 ± 0.012 | 0.733 ± 0.068 | 0.883 ± 0.014 |
|
| |||||
| DSMIL | 0.932 ± 0.023 | 0.930 ± 0.020 | 0.729 ± 0.018 | 0.869 ± 0.008 | 0.925 ± 0.007 |
Acknowledgment:
The work was supported by NIH P41-GM135019, the Semiconductor Research Corporation (SRC), and the Morgridge Institute for Research. YL also acknowledges the support by the UW VCRGE with funding from WARF.
References
- [1].Akbar Shazia and Martel Anne L.. Cluster-Based Learning from Weakly Labeled Bags in Digital Pathology. arXiv:1812.00884 [cs, stat], Nov. 2018. arXiv: 1812.00884.
- [2].Bejnordi Babak Ehteshami, Litjens Geert, Hermsen Meyke, Karssemeijer Nico, and van der Laak Jeroen A. W. M.. A multi-scale superpixel classification approach to the detection of regions of interest in whole slide histopathology images. In Medical Imaging 2015: Digital Pathology, volume 9420, page 94200H. International Society for Optics and Photonics, Mar. 2015. [Google Scholar]
- [3].Campanella Gabriele, Hanna Matthew G., Geneslaw Luke, Miraflor Allen, Silva Vitor Werneck Krauss, Busam Klaus J., Brogi Edi, Reuter Victor E., Klimstra David S., and Fuchs Thomas J.. Clinical-grade computational pathology using weakly supervised deep learning on whole slide images. Nature Medicine, 25(8):1301–1309, Aug. 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Carbonneau Marc-André, Cheplygina Veronika, Granger Eric, and Gagnon Ghyslain. Multiple instance learning: A survey of problem characteristics and applications. Pattern Recognition, 77:329–353, 2018. [Google Scholar]
- [5].Charles R. Qi, Su Hao, Kaichun Mo, and Guibas Leonidas J.. PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation. In 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pages 77–85, Honolulu, HI, July 2017. IEEE. [Google Scholar]
- [6].Chen Po-Hsuan Cameron, Gadepalli Krishna, MacDonald Robert, Liu Yun, Kadowaki Shiro, Nagpal Kunal, Kohlberger Timo, Dean Jeffrey, Corrado Greg S., Hipp Jason D., Mermel Craig H., and Stumpe Martin C.. An augmented reality microscope with real-time artificial intelligence integration for cancer diagnosis. Nature Medicine, 25(9):1453–1457, Sept. 2019. Number: 9 Publisher: Nature Publishing Group. [DOI] [PubMed] [Google Scholar]
- [7].Chen Ting, Kornblith Simon, Norouzi Mohammad, and Hinton Geoffrey. A Simple Framework for Contrastive Learning of Visual Representations. Proceedings of the International Conference on Machine Learning, 1, 2020. [Google Scholar]
- [8].Chikontwe Philip, Kim Meejeong, Nam Soo Jeong, Go Heounjeong, and Park Sang Hyun. Multiple Instance Learning with Center Embeddings for Histopathology Classification. In Martel Anne L., Abolmaesumi Purang, Stoyanov Danail, Mateus Diana, Zuluaga Maria A., Zhou S. Kevin, Racoceanu Daniel, and Joskowicz Leo, editors, Medical Image Computing and Computer Assisted Intervention – MICCAI 2020, Lecture Notes in Computer Science, pages 519–528, Cham, 2020. Springer International Publishing. [Google Scholar]
- [9].Cinbis Ramazan Gokberk, Verbeek Jakob, and Schmid Cordelia. Weakly supervised object localization with multifold multiple instance learning. IEEE transactions on pattern analysis and machine intelligence, 39(1):189–203, 2016. [DOI] [PubMed] [Google Scholar]
- [10].Cornish Toby C., Swapp Ryan E., and Kaplan Keith J.. Whole-slide Imaging: Routine Pathologic Diagnosis. Advances in Anatomic Pathology, 19(3):152, May 2012. [DOI] [PubMed] [Google Scholar]
- [11].Cruz-Roa Angel, Basavanhally Ajay, González Fabio, Gilmore Hannah, Feldman Michael, Ganesan Shridar, Shih Natalie, Tomaszewski John, and Madabhushi Anant. Automatic detection of invasive ductal carcinoma in whole slide images with convolutional neural networks. In Medical Imaging 2014: Digital Pathology, volume 9041, page 904103. International Society for Optics and Photonics, Mar. 2014. [Google Scholar]
- [12].Dehaene Olivier, Camara Axel, Moindrot Olivier, de Lavergne Axel, and Courtiol Pierre. Self-Supervision Closes the Gap Between Weak and Strong Supervision in Histology. arXiv:2012.03583 [cs, eess], Dec. 2020. arXiv: 2012.03583.
- [13].Deng Jia, Dong Wei, Socher Richard, Li Li-Jia, Li Kai, and Fei-Fei Li. ImageNet: A large-scale hierarchical image database. In 2009 IEEE Conference on Computer Vision and Pattern Recognition, pages 248–255, June 2009. ISSN: 1063-6919. [Google Scholar]
- [14].Dietterich Thomas G., Lathrop Richard H., and Lozano-Pérez Tomás. Solving the multiple instance problem with axis-parallel rectangles. Artificial Intelligence, 89(1):31–71, Jan. 1997. [Google Scholar]
- [15].Bejnordi Babak Ehteshami, Veta Mitko, van Diest Paul Johannes, van Ginneken Bram, Karssemeijer Nico, Litjens Geert, van der Laak Jeroen A. W. M., and and the CAMELYON16 Consortium. Diagnostic Assessment of Deep Learning Algorithms for Detection of Lymph Node Metastases in Women With Breast Cancer. JAMA, 318(22):2199–2210, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Feng Ji and Zhou Zhi-Hua. Deep MIML Network. AAAI Conference on Artificial Intelligence, page 7, 2017. [Google Scholar]
- [17].Gao Yi, Liu William, Arjun Shipra, Zhu Liangjia, Ratner Vadim, Kurc Tahsin, Saltz Joel, and Tannenbaum Allen. Multi-scale learning based segmentation of glands in digital colonrectal pathology images. Proceedings of SPIE–the International Society for Optical Engineering, 9791, Feb. 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Hashimoto Noriaki, Fukushima Daisuke, Koga Ryoichi, Takagi Yusuke, Ko Kaho, Kohno Kei, Nakaguro Masato, Nakamura Shigeo, Hontani Hidekata, and Takeuchi Ichiro. Multi-scale Domain-adversarial Multiple-instance CNN for Cancer Subtype Classification with Unannotated Histopathological Images. In 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pages 3851–3860, Seattle, WA, USA, June 2020. IEEE. [Google Scholar]
- [19].He Kaiming, Fan Haoqi, Wu Yuxin, Xie Saining, and Girshick Ross. Momentum contrast for unsupervised visual representation learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 9729–9738, 2020. [Google Scholar]
- [20].He Kaiming, Zhang Xiangyu, Ren Shaoqing, and Sun Jian. Deep Residual Learning for Image Recognition. In 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pages 770–778, Las Vegas, NV, USA, June 2016. IEEE. [Google Scholar]
- [21].Hou Le, Samaras Dimitris, Kurc Tahsin M., Gao Yi, Davis James E., and Saltz Joel H.. Patch-Based Convolutional Neural Network for Whole Slide Tissue Image Classification. In 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pages 2424–2433, Las Vegas, NV, USA, June 2016. IEEE. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Ilse Maximilian, Tomczak Jakub, and Welling Max. Attention-based Deep Multiple Instance Learning. In International Conference on Machine Learning, pages 2127–2136. PMLR, July 2018. ISSN: 2640-3498. [Google Scholar]
- [23].Kandemir Melih and Hamprecht Fred A.. Computer-aided diagnosis from weak supervision: a benchmarking study. Computerized Medical Imaging and Graphics: The Official Journal of the Computerized Medical Imaging Society, 42:44–50, June 2015. [DOI] [PubMed] [Google Scholar]
- [24].Keikhosravi Adib, Li Bin, Liu Yuming, Conklin Matthew W., Loeffler Agnes G., and Eliceiri Kevin W.. Non-disruptive collagen characterization in clinical histopathology using cross-modality image synthesis. Communications Biology, 3(1):1–12, July 2020. Number: 1 Publisher: Nature Publishing Group. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Kingma Diederick P and Ba Jimmy. Adam: A method for stochastic optimization. In International Conference on Learning Representations (ICLR), 2015. [Google Scholar]
- [26].Koohbanani Navid Alemi, Unnikrishnan Balagopal, Khurram Syed Ali, Krishnaswamy Pavitra, and Rajpoot Nasir. Self-Path: Self-supervision for Classification of Pathology Images with Limited Annotations. arXiv:2008.05571 [cs, eess], Aug. 2020. arXiv: 2008.05571. [DOI] [PubMed] [Google Scholar]
- [27].Li Bin, Keikhosravi Adib, Loeffler Agnes G., Eliceiri Kevin W., and Keikhosravi Adib. Single image super-resolution for whole slide image using convolutional neural networks and self-supervised color normalization. Medical Image Analysis, page 101938, Dec. 2020. [DOI] [PubMed] [Google Scholar]
- [28].Lin Tsung-Yi, Dollár Piotr, Girshick Ross, He Kaiming, Hariharan Bharath, and Belongie Serge. Feature pyramid networks for object detection. In CVPR, pages 2117–2125, 2017. [Google Scholar]
- [29].Litjens Geert, Kooi Thijs, Bejnordi Babak Ehteshami, Setio Arnaud Arindra Adiyoso, Ciompi Francesco, Ghafoorian Mohsen, van der Laak Jeroen A. W. M., van Ginneken Bram, and Sánchez Clara I.. A survey on deep learning in medical image analysis. Medical Image Analysis, 42:60–88, Dec. 2017. [DOI] [PubMed] [Google Scholar]
- [30].Liu Yun, Gadepalli Krishna, Norouzi Mohammad, Dahl George E., Kohlberger Timo, Boyko Aleksey, Venugopalan Subhashini, Timofeev Aleksei, Nelson Philip Q., Corrado Greg S., Hipp Jason D., Peng Lily, and Stumpe Martin C.. Detecting Cancer Metastases on Gigapixel Pathology Images. arXiv:1703.02442 [cs], Mar. 2017. arXiv: 1703.02442. [Google Scholar]
- [31].Loshchilov Ilya and Hutter Frank. Sgdr: Stochastic gradient descent with warm restarts. International Conference on Learning Representations (ICLR), 2016. [Google Scholar]
- [32].Lu Ming Y., Chen Richard J., Wang Jingwen, Dillon Debora, and Mahmood Faisal. Semi-Supervised Histology Classification using Deep Multiple Instance Learning and Contrastive Predictive Coding. arXiv:1910.10825 [cs, q-bio], Nov. 2019. arXiv: 1910.10825.
- [33].Maksoud Sam, Zhao Kun, Hobson Peter, Jennings Anthony, and Lovell Brian C.. Sos: Selective objective switch for rapid immunofluorescence whole slide image classification. In CVPR, 2020. [Google Scholar]
- [34].Maron Oded and Lozano-Pérez Tomás. A Framework for Multiple-Instance Learning. In Jordan MI, Kearns MJ, and Solla SA, editors, Advances in Neural Information Processing Systems 10, pages 570–576. MIT Press, 1998. [Google Scholar]
- [35].Hojjat Seyed Mousavi Vishal Monga, Rao Ganesh, and Rao Arvind U. K.. Automated discrimination of lower and higher grade gliomas based on histopathological image analysis. Journal of Pathology Informatics, 6:15, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].van den Oord Aaron, Li Yazhe, and Vinyals Oriol. Representation learning with contrastive predictive coding. arXiv preprint arXiv:1807.03748, 2018.
- [37].Oquab Maxime, Bottou Leon, Laptev Ivan, and Sivic Josef. Is object localization for free? - Weakly-supervised learning with convolutional neural networks. In 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pages 685–694, Boston, MA, USA, June 2015. IEEE. [Google Scholar]
- [38].Pantanowitz Liron, Valenstein Paul N., Evans Andrew J., Kaplan Keith J., Pfeifer John D., Wilbur David C., Collins Laura C., and Colgan Terence J.. Review of the current state of whole slide imaging in pathology. Journal of Pathology Informatics, 2(1):36, Jan. 2011. 1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Pinheiro Pedro O. and Collobert Ronan. From image-level to pixel-level labeling with Convolutional Networks. In 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pages 1713–1721, Boston, MA, USA, June 2015. IEEE. [Google Scholar]
- [40].Quellec Gwenolé, Cazuguel Guy, Cochener Béatrice, and Lamard Mathieu. Multiple-Instance Learning for Medical Image and Video Analysis. IEEE Reviews in Biomedical Engineering, 10:213–234, 2017. Conference Name: IEEE Reviews in Biomedical Engineering. [DOI] [PubMed] [Google Scholar]
- [41].Ronneberger Olaf, Fischer Philipp, and Brox Thomas. U-Net: Convolutional networks for biomedical image segmentation. In MICCAI, pages 234–241. Springer, 2015. [Google Scholar]
- [42].Sabour Sara, Frosst Nicholas, and Hinton Geoffrey E. Dynamic Routing Between Capsules. In Guyon I, Luxburg UV, Bengio S, Wallach H, Fergus R, Vishwanathan S, and Garnett R, editors, Advances in Neural Information Processing Systems 30, pages 3856–3866. Curran Associates, Inc., 2017. [Google Scholar]
- [43].Scarselli Franco, Gori Marco, Tsoi Ah Chung, Hagenbuchner Markus, and Monfardini Gabriele. The Graph Neural Network Model. IEEE Transactions on Neural Networks, 20(1):61–80, Jan. 2009. Conference Name: IEEE Transactions on Neural Networks. [DOI] [PubMed] [Google Scholar]
- [44].Sirinukunwattana Korsuk, Pluim Josien P. W., Chen Hao, Qi Xiaojuan, Heng Pheng-Ann, Guo Yun Bo, Wang Li Yang, Matuszewski Bogdan J., Bruni Elia, Sanchez Urko, Böhm Anton, Ronneberger Olaf, Cheikh Bassem Ben, Racoceanu Daniel, Kainz Philipp, Pfeiffer Michael, Urschler Martin, Snead David R. J., and Rajpoot Nasir M.. Gland segmentation in colon histology images: The glas challenge contest. Medical Image Analysis, 35:489–502, Jan. 2017. [DOI] [PubMed] [Google Scholar]
- [45].Tang Peng, Wang Xinggang, Bai Xiang, and Liu Wenyu. Multiple instance detection network with online instance classifier refinement. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 2843–2851, 2017. [Google Scholar]
- [46].Tokunaga Hiroki, Teramoto Yuki, Yoshizawa Akihiko, and Bise Ryoma. Adaptive Weighting Multi-Field-Of-View CNN for Semantic Segmentation in Pathology. In 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pages 12589–12598, Long Beach, CA, USA, June 2019. IEEE. [Google Scholar]
- [47].Tu Ming, Huang Jing, He Xiaodong, and Zhou Bowen. Multiple instance learning with graph neural networks. arXiv:1906.04881 [cs, stat], June 2019. arXiv: 1906.04881.
- [48].Vaswani Ashish, Shazeer Noam, Parmar Niki, Uszkoreit Jakob, Jones Llion, Gomez Aidan N, Kaiser Łukasz, and Polosukhin Illia. Attention is All you Need. In Guyon I, Luxburg UV, Bengio S, Wallach H, Fergus R, Vishwanathan S, and Garnett R, editors, Advances in Neural Information Processing Systems 30, pages 5998–6008. Curran Associates, Inc., 2017. [Google Scholar]
- [49].Wan Fang, Liu Chang, Ke Wei, Ji Xiangyang, Jiao Jianbin, and Ye Qixiang. C-mil: Continuation multiple instance learning for weakly supervised object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 2199–2208, 2019. [Google Scholar]
- [50].Wang Dayong, Khosla Aditya, Gargeya Rishab, Irshad Humayun, and Beck Andrew H.. Deep Learning for Identifying Metastatic Breast Cancer. arXiv:1606.05718 [cs, q-bio], June 2016. arXiv: 1606.05718.
- [51].Wang Xiaolong, Girshick Ross, Gupta Abhinav, and He Kaiming. Non-local Neural Networks. In 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 7794–7803, Salt Lake City, UT, USA, June 2018. IEEE. [Google Scholar]
- [52].Wang Xinggang, Yan Yongluan, Tang Peng, Bai Xiang, and Liu Wenyu. Revisiting Multiple Instance Neural Networks. Pattern Recognition, 74:15–24, Feb. 2018. [Google Scholar]
- [53].Xu Yan, Jia Zhipeng, Ai Yuqing, Zhang Fang, Lai Maode, and Chang Eric I-Chao. Deep convolutional activation features for large scale Brain Tumor histopathology image classification and segmentation. In 2015 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), pages 947–951, Apr. 2015. ISSN: 2379-190X. [Google Scholar]
- [54].Xu Yan, Zhu Jun-Yan, Eric I, Chang Chao, Lai Maode, and Tu Zhuowen. Weakly supervised histopathology cancer image segmentation and classification. Medical image analysis, 18(3):591–604, 2014. [DOI] [PubMed] [Google Scholar]
- [55].Yan Yongluan, Wang Xinggang, Guo Xiaojie, Fang Jiemin, Liu Wenyu, and Huang Junzhou. Deep Multi-instance Learning with Dynamic Pooling. In Zhu Jun and Takeuchi Ichiro, editors, ACML, volume 95 of Proceedings of Machine Learning Research, pages 662–677. PMLR, Nov. 2018. [Google Scholar]
- [56].Zhu Zhen, Xu Mengdu, Bai Song, Huang Tengteng, and Bai Xiang. Asymmetric Non-Local Neural Networks for Semantic Segmentation. In 2019 IEEE/CVF International Conference on Computer Vision (ICCV), pages 593–602, Seoul, Korea (South), Oct. 2019. IEEE. [Google Scholar]


